
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
- 材料的性能永远不能被精确知道(3)不符合设计的受钢筋,可能导致易碎混凝土受压破坏即使rho;可能稍微小于rho;b(4)钢筋的实际受力面积,考虑到标准的受力钢筋规格,将一直等于或者大于需要的,根据可选择的配筋率rho;,存在的趋势。(5)并且用低水平的rho;的梁提供的额外的延展性实际上增加了误差允许范围,并且,因此为失效提供了先前的警告。
D.ACI 规范关于梁的规定
然而,构件名义应力可能由力学公式计算出来,由单独的力学计算不能建立起安全的最大配筋率界限,这些极限由ACI规范规定,这种极限采用两种方面,第一,规范规定最小拉力钢筋应变由梁的名义应力规定。第二,规范规定强度降低系数有可能取决于名义强度下的拉应变。两种极限都是基于净拉伸应变 ,根据配筋最远面临的混凝土最下方的挤压深度。净拉伸应变是不受预应力、温度和收缩影响的。对于单层受力钢筋的梁,与钢筋的形心深度是相同的,对于多层受力钢筋,远远大于钢筋形心。在等式(3.27)中用代替,用 代替 ,净拉伸应变应该被计算为
(3.29)
然后根据等式(3.28),对于生产要求选择一个合适的净拉伸应变得到的配筋率为
(3.30a)
为了确保加固不足的问题,ACI规范10.3.5建立了一个最小净拉伸应变,t在名义构件强度0.004对于构件对象对轴向荷载小于0.1fcrsquo;Ag,Ag是横截面总面积,通过比较y钢筋应变处于平衡状态,对fy=60000psi为0.00207和对fy=75000psi为0.00259。
将t=0.004代入等式(3.30a)可导出一个ACI规范对于梁所允许的最大配筋率
(3.30b)
最大配筋率是对于单层受力钢筋是确定的,对于dt大于d的多层受力钢筋是略显保守的,因此t0.004确保钢筋是拉紧而屈服,在fs=fy时失效,并且名义上的挠曲强度(根据图3.11)可得
(3.31)
在上式中
(3.32)
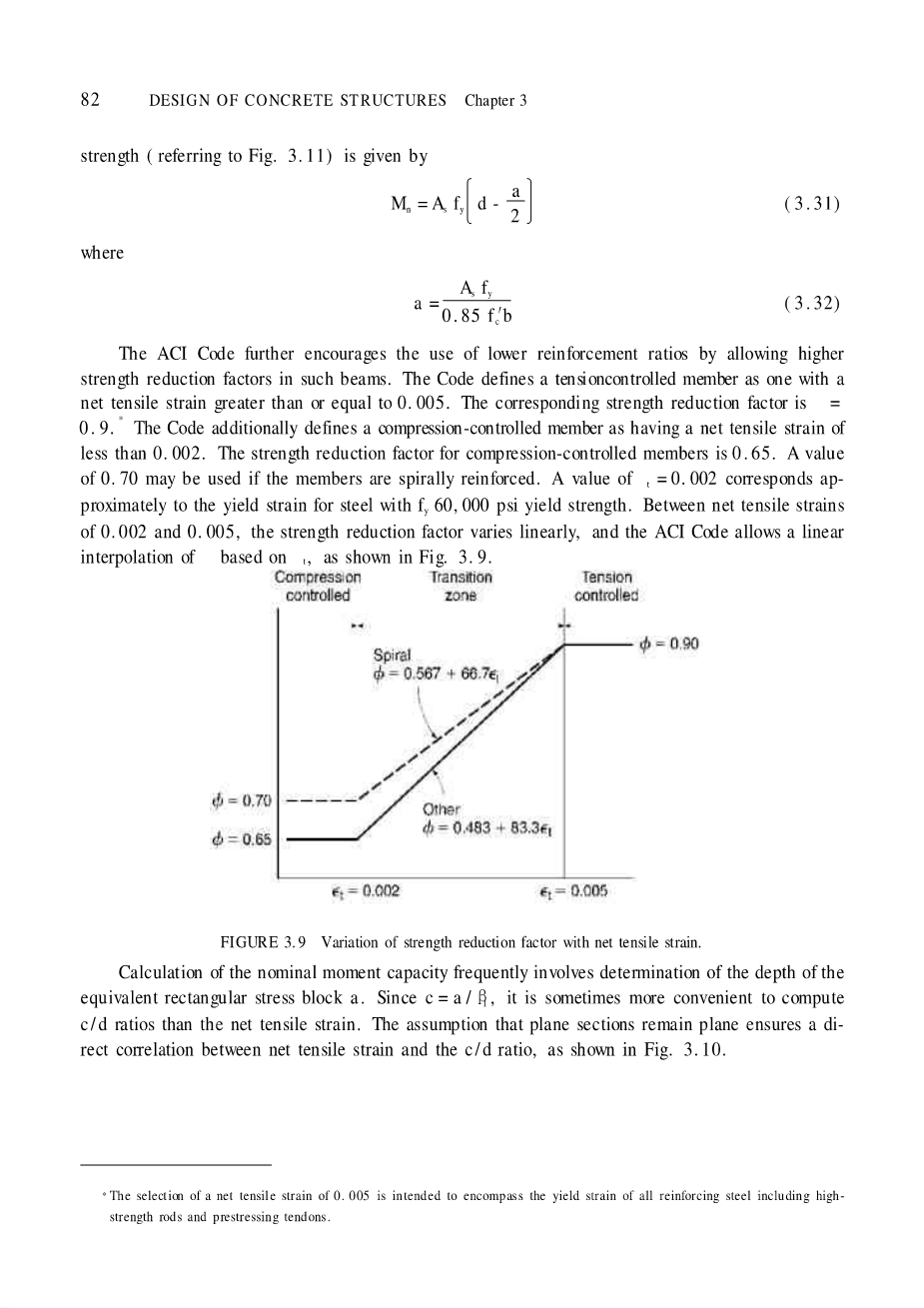
ACI规范更多的鼓励在这样的梁中通过允许更高的强度折减系数来降低配筋率,规范定义了一个由拉力控制的量,作为一个和净拉伸应变相关的大于或者等于0.005相关的量,相关的强度折减系数 =0.9,规范另外定义了一个由受压控制的系数当净拉伸应变小于0.002,这时的强度折减系数是0.65,。当构件为螺旋强化时可以使用0.70,t=0.002可以使用当趋近钢筋屈服,在fy60000psi屈服强度的条件下。净拉伸应变在0.002和0.005之间,强度折减系数呈线性分布,并且规范允许根据t进行线性插值,由图3.9可知
图3.9 与净拉伸应变对应的强度折减系数
计算名义弯矩承载力经常涉及的等效矩形应力测定的深度块a。由于c=a/beta;1,有时计算c/d比率比测净拉伸应变更方便,平面部分保持平面的假设确保了净拉伸应变与c/d比率的相关性,如图3.10所示。
图3.10 净拉伸应变和c/dt比率的图像
示例3.4
采用等效矩形应力分布,直接计算以前分析例3.3中梁的的名义强度。
解。应力、内力和应变分布如图3.11所示,最大配筋率从等式(3.30b)可知
并且与实际的配筋率0.0103相比证明构件是加固不足的并将导致钢筋屈服破坏。相同的钢筋区域深度可以由平衡状态下求得,C=T,因此0.85fcrsquo; ab=Asfy, 或者,到中轴线的距离,通过定义矩形应力区域,
标称力矩为
这个简单的和直接的数值分析结果,基于等效矩形应力分布,与在第3.3c部分确定的一般强度分析方法是相同的。
结合等式(3.31)和(3.32)以及以下等式,对于设计是很方便的,注明As=rho;bd,等式(3.32)能被写成
(3.33)
这个式子然后被替换进等式(3.31)得到
(3.34)
上式与来自于3.3c部分等式(3.20b)相同,这个基本的方程可以被大大的简化为下式:
(3.35)
其中
(3.36)
抗弯系数R仅仅取决于配筋率和材料强度并且很容易制成表格,在附录A中的表格A.5a和A.5b给定R定值对于普通的钢筋和混凝土组合并且充分的实际的配筋率区间。
根据ACI规范的安全规定,通过增加强度折减系数名义抗弯强度将会减低,来达到设计强度:
(3.37)
或者,可用下式代替
(3.38)
或者
(3.39)
示例3.4(接上文)
计算示例3.4中梁的设计弯矩承载能力。
解。到中间轴的距离c=4.92,=0.003(23-4.92)/4.92=0.011来自等式(3.28)。>0.005,所以 =0.90并且可得设计承载弯矩
e最小配筋率
另一种失效的情况可能发生在非常少的配筋梁中。如果易碎裂部分的抗弯刚度比先前的不是脆性部分产生开裂的弯矩小,那么梁将会立即毁坏并且不带有任何的预兆在第一种弯曲破坏下。为了应对这种毁坏,为了这种配筋率通过等效的开裂弯矩将建立一种更低的极限,计算破裂混凝土系数(2.9部分),为了加强破裂部分。
对于矩形部分已有宽度b,总深度h,和有效深度d(见图3.2b),截面模量相当于张力是bhsup2;/6。对于典型的横截面,h/d=1.1是理想的假设并且弯曲破坏在内部的水平高度是0.95d。如果像往常一样断裂系数取 ,那么一种等同于开裂构件的分析的抗弯刚度的结果是
(3.40a)
这种发展可以推广到具有T截面的梁(见部分3.8和图3.15)。相应的方程取决于横截面的比例和梁是否边缘受拉或者受压。对于边缘受压弯曲的典型比例的T形梁,分析将会证明最小的钢筋面积应是
(3.40b)
其中bw是网或者干的宽度,投射在下面的板。那些在边缘受拉的T形梁,通过相同的分析,最小的钢截面面积是
(3.40c)
ACI规范要求的最小钢筋面积是根据刚才讨论的结果,但也有一些不同。根据ACI10.5,在任何部分,拉伸配筋是需要分析的,除了一些例外,提供的面积一定不能小于
(3.41)
这适用于正面和反面的弯曲部分。这包含额外的200d/fy的限制,仅仅是经验的原因。这种情况发生在最小配筋率0.005,那些应用在早些的规范中为了达到共同的材料强度。注意到在等式(3.41)中bw被应用;对于矩形部分bw=b是很好理解的。更多的注意到ACI系数3与2.7在保守范围内对比是相同的,(3.40b)对于边缘受压的T形梁,和非常保守的当应用于矩形梁部分,合理分析给出1.8在等式(3.40a)。这可能反映了一种观点,最小的钢对于T形梁最不安全的部分(实际上在矩形部分,正如在部分3.8c所讨论的那样)应该不比安全的弯曲的弯矩真的一般很小的地方小。
ACI规范10.5将静定的T形梁边缘受拉作为一种非常特殊的情况,在这种情况下最小的钢筋面积与等式(3.41)中用2bw代替bw或者边缘宽度更小的那个相比是一样的或者说是更加优秀的。
注意到ACI规范中等式(3.41)方便的表达了对于最小的抗拉配筋率而言,rho;min通过bwd被分成两部分。
根据ACI规范10.5,等式(3.41)的未知数可以不知道在每一部分抗拉区域加强筋至少比计算所需要的多1/3的情况下。这提供了一种更有效的配筋对于大型构件来说,像主受力梁,通常的方程计算出会需要过量的钢筋。
对于结构板厚度均匀的构件,最小的受拉配筋受跨度方向的收缩和温度钢材的控制(见部分13.3和表格13.2),并且以上的最小的不需要利用,像这样的钢筋最小的部分比总共的板厚度小三倍,或者是18英寸。
F.矩形梁的分析和设计实例
弯曲问题大致可以被分为分析问题和设计问题,在分析问题时,截面尺寸,配筋,和材料强度是已知的,弯矩承载能力是要求得的。在设计问题方面,需要的弯矩承载能力是已知的,材料强度和截面尺寸,配筋是要设计的。例3.5和例3.6分别列举了分析和设计问题。
示例3.5抗弯强度已知,一个矩形梁宽12英尺,实际深度17.5英尺。配筋用4号No.9单排。如果fy=60000psi和fcrsquo;=4000psi,那么根据ACI规范,在设计中计算弯曲强度和最大弯矩可以应用?
解。从附录A中表A.2可知,4号No.9钢筋是4平方英寸。因此,实际的配筋率rho;=4.00/(12*17.5)=0.0190。这个值小于从等式(3.30b)得到的最大值
所以将会受拉屈服毁坏。对于这种配筋不足的梁,从等式(3.32)可得,
并且从等式(3.31),
到中轴线的距离c=a/beta;1=5.88/0.85=6.92。净拉伸应变t=u(d-c)/c=0.0038*(17.5-6.92=0.00458)=0.00458>0.004;但是小于0.005;因此,强度降低因数必须调整。在图3.9中使用线性内插得 =0.87,因此设计强度是
ACI规范限制的配筋率是
可知,对于此梁是安全的。
示例3.6
具体尺寸和钢筋截面积限制已知。找到横截面的具体尺寸和需要的钢筋的位置对于一个简支矩形梁跨度是15ft承载了一个已知静荷载1.27kips/ft并且有一个动荷载为2.15kips/ft,材料的强度分别为fcrsquo;=4000psi和fy=60000psi。
解。工作荷载达到设计极限荷载是设计梁的第一个荷载应用条件,对应的弯矩如下:
具体尺寸将决定设计者的所选择的配筋率。为了使混凝土尺寸最小化,应该选择最大的允许的配筋率。设=0.9,最大配筋率对应的净拉伸应变0.005被选择(见图3.9)。然后从等式(3.30a)
用等式(3.30b)给rho;max=0.0206,但是这将需要更低强度减少因数。设置需要的弯曲强度等于设计强度从等式(3.38,),并且用rho;和材料强度代替选择的值,
从
一个宽b=10in和d=14.3in,在需要上是安全的。这是需要的钢筋面积由选择的配筋率到需要的具体尺寸可得
2根No.10钢筋为2.45insup2;,与需要的面积是非常接近的。
假设从混凝土覆盖层到钢筋组的重心为2.5in,则需要的总深度h=16.8in。在实际联系中,然而,具体尺寸b和h是围绕着接近尺寸上下波动的,并且最接近的多个为2in,见3.5章。实际d需要从h中减掉需要的混凝土层。对于这个例子,b=10in,h=18in,导致深度d=15.5in。然后提高经济效益将变成可能,根据实际的,大一点的,有效的深度来完善钢筋面积。可以通过求解等式(3.38)用Mn=Mu直接得到修改后的钢筋。更快速地解将会得到通过迭
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[136852],资料为PDF文档或Word文档,PDF文档可免费转换为Word


