英语原文共 20 页
相位成像
4.1简介
相位成像可能是原子力显微术(AFM)领域最著名和应用最广泛的模式之一。其广泛流行有几个原因。首先,它是一种简单的方法,它是一种轻敲模式(也被称为幅度调制模式,间歇接触模式)下的信息收集通道,并且不需要后期处理。其次,由于对材料特性敏感,它是最容易实现的模式之一,这也是AFM除了用于提供纳米级形貌信息的主要吸引力之一。已经有大量的研究试图将相位信号与实际材料特性相关联,例如储能模量,损耗模量和损耗角正切。然而,相位成像相当复杂,其含义的解释仍然存在广泛的争论和研究。
从根本上说,在相位成像中测量的相移是悬臂梁耗散到材料中的能量的量度。它是保守和非保守针尖-样品相互作用力的测量(见第3章),它实际上取决于许多因素,包括粘弹性,粘附力,毛细管力和接触区域。也就是说,根据应用部分中的大量示例证明,相位成像是一个非常方便和利于使用的根据材料属性区分材料的方法。
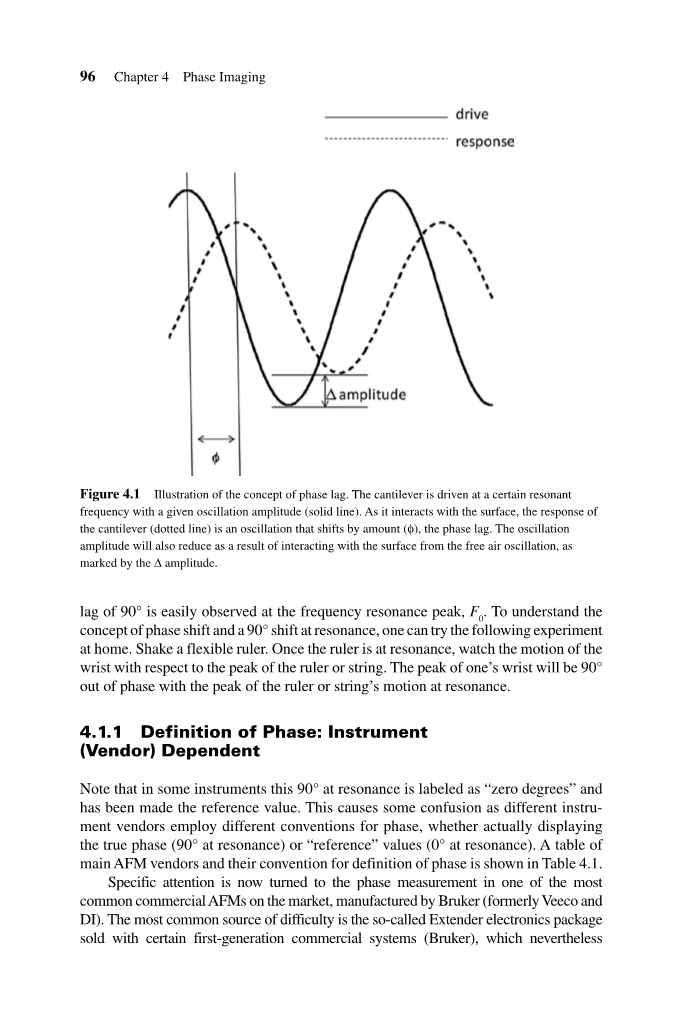
相移始终相对于一个参考进行测量,在这种情况下是相对于驱动的悬臂梁。悬臂梁以共振频率进行驱动,并以用户设定的给定振幅与样品相互作用。然后通过与样品相互作用诱导相移(Phi;),如图4.1所示。当针尖通过栅格化扫描表面时,相移作为一个通道进行成像。在谐振时,具有阻尼的驱动谐振子的相位滞于驱动力或激励力为90°,如图4.2所示,其中在频率共振峰值F0处容易观察到90°的相位滞后。为了理解相移的概念和共振时的90°偏移,可以在家中尝试以下实验。摇动灵活的尺子。一旦标尺处于共振状态,观察手腕相对于标尺或弦的峰值的运动。一个人手腕的峰值将与标尺的峰值或弦的共振运动成90°异相。
4.1.1相位的定义:仪器(供应商)相关
请注意,在某些仪器中,此共振90°标记为“零度”,并已作为参考值。这会引起一些混乱,因为不同的仪器供应商对相位采用不同的约定,无论是实际显示真实相位(共振时为90°)还是“参考”值(共振时为0°)。表4.1列出了主要AFM供应商的表格及其定义相的惯例。现在最受关注的相位测量市场上,最普遍的一种商业AFM是由Bruker(前身为Veeco和DI)制造。最常见的困难来源于某些第一代商业系统(Bruker)一起销售的所谓扩展器电子组件的东西,但仍然是常用的(即,仍然是有价值的仪器)。相位扩展器单元是许多早期控制器(NanoscopeIII-IV)的附加装置,其设计目的不仅仅是测量相位本身。真实相位的测量需要锁定放大器或类似的复杂装置来跟踪两个正弦波的相对时间偏移,此外,其频率范围可扩展到数百千赫兹。但扩展器可以进行校准,以提供非常接近真实相位的数字,用于大多数感兴趣的测量。感兴趣的话,第4.3.3节提供了这种校准的详细说明。
现在讨论与相位成像相关的工件和挑战。
4.2双稳态:吸引和排斥模态
相位可以在控制形貌成像中起到关键的诊断作用。在科学文献中已经确定,与样品表面相互作用的振荡AFM针尖(和悬臂梁)可以是双稳态的。这意味着对样品的针尖给定(平均)Z值,可能出现两种可能状态中的一种。我们将这称为(纯)吸引和(纯)排斥状态。(对于给定的Z值,一些作者使用术语高振幅或低振幅状态来表示。)这个概念意味着在AFM成像期间(即,在固定的设定点振幅),高度存在两种可能性:一种是净针尖-样品相互作用是排斥的,另一种是净相互作用是有吸引力的(即,尖端不具有吸引力)靠近表面)。双稳态意味着在任何位置振荡针尖可以沉降到一种状态或另一种状态,净吸引力或排斥性。在每个像素处发生足够的振荡,可以达到独特的动态平衡;也就是说,振荡器可以在一个状态或另一个状态下稳定在图像的特定子区域中,与局部样本属性相对应。
由双稳态引起的伪影对于相位成像的从业者而言是众所周知的,并且是造成许多观察到的对比度反转伪影的原因。当进行相位成像时,了解图像是否在纯吸引或纯排斥状态下收集是非常重要的。两种不同方案中的双稳态和操作可能是解释模态-相位图像(高度通道,相位通道,如下面所描述的)的最重要的混淆源。幸运的是,相位信号提供了一种有效的操作方式。
在纯吸引系统中,相位大于90°;在纯排斥状态下,相位小于90°。由于不同的供应商将共振阶段定义为不同的值(例如,90°或0°),因此不同供应商制造的AFM的纯吸引和纯排斥的不同方案也包括在表4.1中。这两种状态都在网络术语中提及,例如,纯吸引状态也可以有相互之间的排斥,但纯相互作用是吸引的。在吸引状态下消耗的能量远远少于排斥状态。这在典型的硬表面(例如,硅)上的吸引状态下可以容易地理解,因为这对应于非接触成像,其中针尖实际上没有与样品接触,因此没有真正的能量耗散途径。此外,由于该状态下针尖磨损最小化,通常保留针尖形状更好。另一方面,较大的针尖或磨损的针尖将比尖锐的针尖具有更大的吸引力。
幸运的是,有几个实验旋钮可以在纯吸引和纯排斥状态之间进行调整。驱动频率是第一个参数,其中略高于共振的驱动有利于吸引的状态,而略低于共振的驱动有利于排斥状态。较大的振荡幅度(由驱动电压控制)意味着更多的动能,因此也有利于在有吸引力的制度下排斥。幅度设定点是在较低幅度设定点电压将有利于排斥相互作用并且较高幅度设定点电压(即,更接近自由空气振荡设定点的设定点)将有利于有吸引力的相互作用的状态之间调节的最终参数。
图4.3和图4.3中的数据图4.4举例说明了在水溶液中在裂解云母上浇铸的聚乙烯醇超薄膜上的吸引和排斥状态的双稳性问题。这些薄膜含有三个不同性质的特征域。第一层完全覆盖基材并牢固粘附。两种不连续的第二层畴的结晶度不同;1 nm厚的少数区域显然是高度结晶的(在接触模式下是脆性的并且表现出与扫描速度无关的摩擦)。网状(~3 nm厚)的多数组成部分的性质(即摩擦,相,粘性)更不均匀。在图4.3中,我们分别标记了这些层1,2和3。对于谐振时自由振荡幅度的三种情况中的每一种示出了高度和相位图像:(a)14 nm,(b)10 nm和(c)4 nm。在所有情况下设定点幅度为自由值的70%,驱动频率为315.16 kHz,即低于共振频率315.46 kHz(标称弹簧常数40 N/m)的0.30 kHz。在每个相位图像中,色标被偏移以提供期望的对比度。
图4.4中的相位分布图量化了图4.3的相位图像(真实相位)。图4.3和图4.4展示了动态原子力显微术的物理衍生伪影:表观相对高度的显著变化,从域到域,是在吸引和排斥状态之间切换的结果。例(b)的相位值的广泛分布分布表明图像内的主要吸引和排斥动态的共存。例(a)和(c)的阶段分布受到更多限制,并且主要对应于吸引状态(c)或排斥状态(a),而不是两者。(b)中最亮的相域显示与相邻区域相比凹陷约0.3 nm的“高度”;而在(a)和(c)中,与相邻区域相比,这些相同的区域相反提升了约1 nm。此外,(a)和(c)项与接触和力曲线映射模式(对于这种聚合物)的观察结果一致系统没有问题,即不产生有害的剪切力)。显然,在(b)情况下给出高度图像时出现了操作性“错误”:在图像上共存两个动态平衡状态,特定于与针尖相互作用的材料类型。显然,这必须避免,并且这样做的一种方法是根据自由振荡幅度(通过驱动振幅)改变振荡器的动能同时保持设定点振幅恒定为自由振荡振幅的一部分。在该示例中,可以采用更大或更小的动能(通过更大或更小的驱动振幅)来稳定图像上的单个稳定状态。
区域特定的相互作用机制(主导吸引力或排斥相互作用的空间域)不一定是由材料特性的不均匀性引起的。表面形状也会导致这种伪影。即使在均质(属性)材料中,如果存在与针尖曲率半径类似于的波谷,那么山谷中的吸引力将明显大于平面或波峰上的吸引。因此,除了在吸引力更强的波谷中,选择用于稳定排斥状态的参数都可以起作用;在平坦表面上以排斥状态稳定的振荡器可以转变为谷中的吸引力状态。(类似地,稳定在平坦表面上的吸引区域的振荡器可能会转变为波峰上的排斥状态,其中吸引力较弱。)图4.5举例说明了多晶金表面的这种情况。在(a)中,选择参数以稳定排斥状态(通过使用标称k=40 N/m悬臂梁,在50-60 nm之间的自由振荡幅度下驱动低于共振)。但是在得到的高度幅度相位图像中,在几个窄谷处,振荡器切换到吸引状态(相位图像中的暗对比度)。人们发现了这个地区情况下,当悬臂梁高于共振时,净吸引力大大增加(b)中。边界划分净吸引或净排斥互动的领域在幅度图像中也可见。
同样重要的是要注意,远程静电力会对动态AFM中的吸引和排斥的相互作用产生显著影响。可以在针尖和样品之间施加电压偏差,以有意产生这种远程静电力,相关到针尖-样品系统的电容。或者可以选择外部偏压以使表面电位的固有差异(即,金属的功函数)无效,以便消除远程力。因此,即使仅对表面形貌感兴趣,偏置针尖或样品的自由度对于普通动态AFM来说可能是重要的,特别是对于高导电性材料,例如图4.5中的金。如果没有补偿,远程静电力会降低排斥状态的稳定性。实际上,图4.5(a)中谷中的纯吸引的存在部分是由于来自不同尖端和样品电位的静电力。如果一个人试图在有吸引力的政权内形象,那么差异就在于表面电位可以稳定这种状态;但是这些力的较大范围会导致“飞行高度”显著增加,从而导致地形图像的模糊。在决定是否引用外部偏差时,用户需要根据被成像表面的实际情况来权衡利弊。
可以说,评估相互作用机制的最明确的测量是动态力曲线或幅度和相位与Z曲线(AP-Z)。这些单点测量曲线将在第3章中详细讨论AP-Z曲线是单点力距离曲线(F-Z),其在共振时悬臂梁振荡时进行,使得幅度和相位被测量为针尖-样本间隙的函数。
在AP-Z曲线中很容易观察到吸引和排斥性状态之间的跳跃。图4.6显示了五个重叠的AP-Z,这是在使用硅尖端和刚性矩形悬臂的未经处理的硅晶片上在五个不同的自由振荡幅度A0(范围从7.7到23.6 nm)的过程中获得的(k〜40 N/m时,Qasymp;400)。振荡器以其共振频率f0=315.46 kHz驱动,使得超过针尖-样品相互作用的Z的相位读数为90°。在接近过程中,振幅[图4.6(a)]在针尖-样品相互作用时减小;最终振幅突然增加~1 nm,然后再次以略微陡峭的斜率减小。相应地,相位数据[图4.6(b)]示出了在幅度突然增加的Z的相同值处的显著上跃。这告诉我们,向~1 nm更高幅度的过渡产生了从吸引到排斥状态的转变。(这就是低幅和高幅状态的替代命名法。)
在图4.6中的五个案例中,有一个注意到跳跃发生在非常不同的A/A0值。具体地说,当悬臂梁具有大量动能时,排斥状态下主要是大范围的振幅,而当悬臂梁具有少量动能时,则具有小范围的振幅。原则上可以选择设定点幅度A,其产生净吸引力或净排斥状态。对于常用值A/A0=0.9,在图4.6(a)中用水平虚线标记三种情况,产生吸引或排斥状态,如原始阶段的零点相应的相位值(用垂直箭头标记)所示。在这三种情况的中间成像的尝试将是有问题的:A/A0=0.9的所选幅度将对应于Z的两个值,净排斥(较低Z)或净吸引(较高Z)。
必须认识到,在异质表面上,AP-Z曲线可能取决于(X,Y)位置;因此,振荡器从吸引转变为排斥的振幅值可随位置而变化。通常需要选择不接近转变的设定点振幅值,预期转变发生的幅度可能随着局部表面曲率从一个位置变化到另一个位置。此外,如果无意中达到转换,则振荡器可以保持“锁定”在新状态,直到达到非常不同类型的位置。“锁定”是由于延伸时的滞后,然后是Z的缩回,并且当在接近期间与收缩期间的数据进行比较时,一般可以在AP-Z曲线中观察到。
将振荡器驱动到略低于共振频率是稳定排斥状态的常用方法。同样,AP-Z曲线可用于通过改变从一个数据集到下一个数据集的驱动频率来探索此行为。图4.7叠加了在共振附近的15个不同驱动频率的接近过程中获得的Z相曲线。这些数据是在类似于图4.3(区域1)的聚乙烯醇(PVA)薄膜上获得的,使用类似的针尖-悬臂梁。当以共振频率f0驱动时,随着Z减小,在Zasymp;28 nm处存在从吸引到排斥状态的跳跃不连续性。当以最低频率f-驱动时,在共振以下约0.25 kHz处,在接近期间在针尖-样品相互作用时看到相位突然减小,但是随着Z减小,相位继续增加。当以频率f 行驶时,相位单调减小为Z减少,缺乏向排斥状态的过渡。中间驱动频率的行为在f 和f-的情况之间进行插值。
上述任何策略(驱动频率的选择,自由振荡幅度,设定点幅度)是否足以稳定整个图像的给定状态也是一个重要的问题。出于这个原因,AP-Z曲线映射可以阐明状态切换发生的程度。此外,可以利用AP-Z曲线映射(使用自定义算法)来生成校正高度映射,该映射不仅可以解决切换现象,还可以量化顺应性(压痕)效应。
我们的第一个AP-Z曲线映射示例是另一个PV的超薄膜,与图4.3中的相似。图4.8显示了传统的高度(a)和相位(b)图像。已经确定了相同的三个特征子区域:第一层大约1 nm厚(1)和两种类型的第二层域,其表现出相对低和高的耗散(2和3)。(b)中的相位对比太强:80°从最暗中分离最亮,最明亮对应于振荡器的纯排斥性位移,而最暗的对应于净吸引的位移。图4.8(c)包含三对原始AP-Z曲线,它们代表区域1-3的行为。在获取AP-Z曲线期间缩回的触发是来自自由振荡值1.87 V的幅度信号的1.25 V减小。检查相位Z曲线,可以看出从三个测量位置之间的相互作用开始(相位急剧下降与降低Z)到最终接近点的Z位移实际上是
资料编号:[3679]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。