
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
第五章 挠曲:T梁、受压钢筋梁和特殊情况
5-1介绍
第四章提出了钢筋混凝土的弯曲理论,并将其应用于受拉区受弯钢筋矩形梁。混凝土梁通常是T形或形,有时在受拉区和受压区都有钢筋。在本章中,会将弯曲理论扩展到这些类型的问题。
由于零应变轴(中性轴)通常不平行于合成力矩作用的轴,因此横截面与加载轴不对称的梁和弯曲于两个轴的梁需要做特殊处理。第5-4节中讨论了此类梁的分析。
当梁具有多层张拉钢筋分布在梁的深度上,或由两种类型的混凝土构成,或包含非弹塑性钢筋时,计算中必须考虑应变兼容性。这在第5-5节中有讨论。
5-2 T型梁
T型梁的实际应用
在图5-1所示的楼板系统中,假定楼板将荷载沿一个方向传递给垂直方向承受荷载的梁。在施工期间,在浇筑楼板中的混凝土之前,应先浇筑柱中的混凝土,并使其硬化(ACI第6.4.5节)。在下一个操作中,应在楼板中浇筑混凝土。以及放置整体浇注的梁(ACI第6.4.6节)。因此,如图5-1中的阴影所示,板用作梁的上翼缘。这种梁称为T型梁。内梁AB两侧有翼缘,拱肩梁CD仅一侧有翼缘,也称为T型梁。
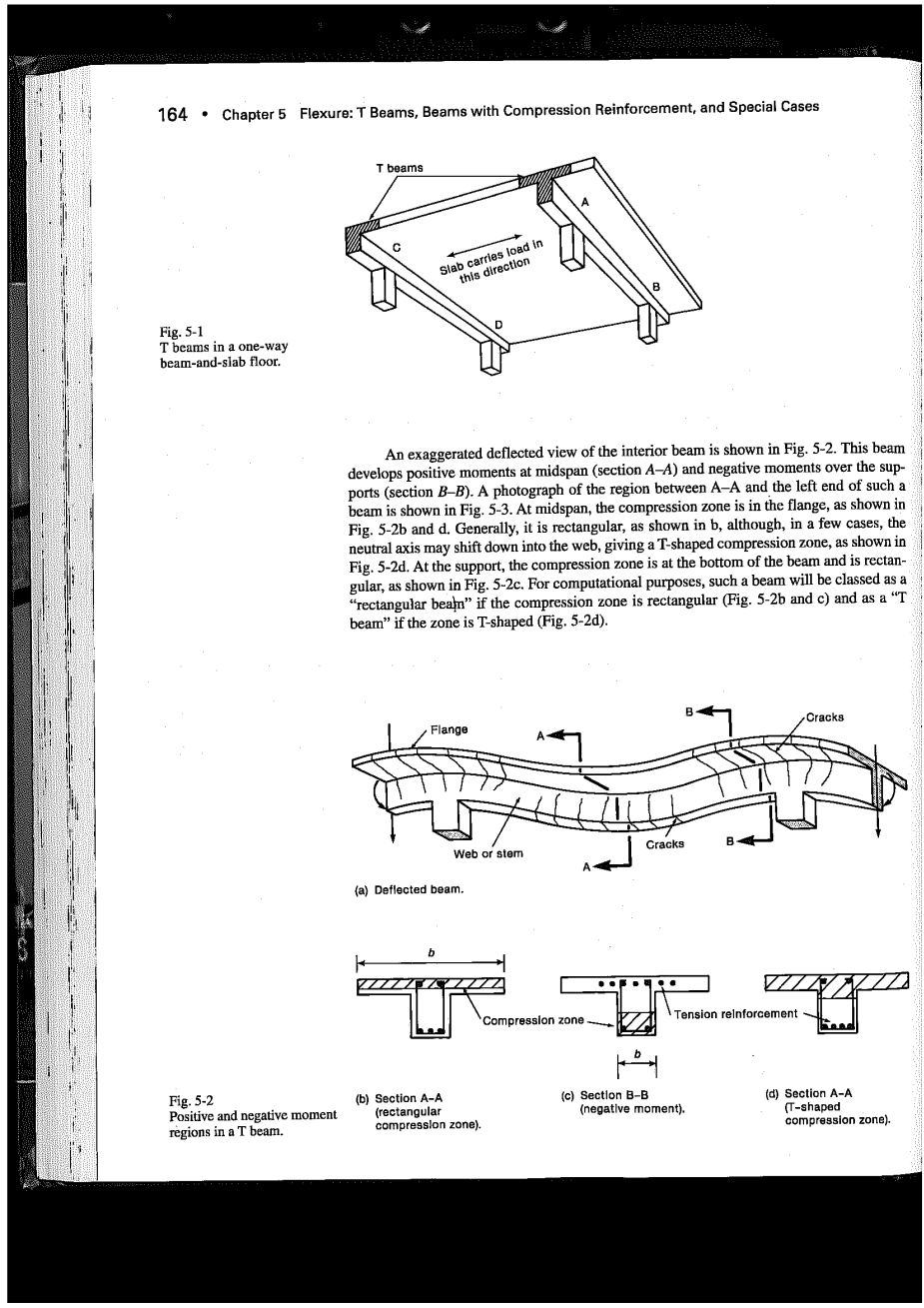
图5-2所示为内梁的放大偏转视图。该梁在跨中(截面A-A)产生正弯矩,在支座(截面B-B)产生负弯矩。图5-3显示了截面A-A和此类梁左端之间区域的照片。在跨中,压缩区域位于翼缘内,如图5-2b和图d所示。通常情况下,它是矩形的,如图b所示,但是在少数情况下,中性轴可能会向下移动到腹板上,形成一个压缩区,如图5-2d所示。在支架处,压缩区位于梁的底部,是矩形的,如图5-2c所示。为了计算方便,如果压缩区是矩形的(图5-2b和图c),则这种梁被称为“矩形梁”,如果压缩区是T形的(图5-2d),则被归类为“T型梁”。
通常情况下,梁板楼面包括由梁支撑的板,而梁又由称为主梁的其它梁支撑(图5-4)。同样,柱顶部以上的所有混凝土都是一次性浇筑的。请注意,板用作梁和主梁的翼缘。
有效翼缘宽度和横向钢筋
作用在简支T型梁翼缘上的力如图5-5a所示。在支座处,翼缘无压应力,但在跨中处,全宽受压应力。如图5-5a所示,过渡需要在腹板-翼缘界面上施加水平剪切应力。因此,存在“剪切滞后”效应,且最靠近腹板的翼缘部分的应力比远处的部分更高,如图5-5a和图5-6所示。
图5-6显示了在最大正弯矩截面上形成一系列的平行于梁翼缘的板中弯曲压应力的分布情况。压缩应力在每个腹板上是最大的,在腹板之间下降。对于支座,从最大到最小的变化更加明显。
当正弯矩部分成比例时,使用“有效宽度”(图5-6b)。这是宽度b,当均匀地受力于时,给出的压缩力是在宽度为b的实际压缩区中产生的。
ACI第8.10节给出了为了设计目的而估算此宽度的规则。对于内梁,ACI第8.10.2节规定:
1、作为T型梁翼缘的板的有效宽度不得超过梁跨度的四分之一。
2、腹板两侧的有效悬挑板宽度不得超过板厚的8倍或与下一梁腹板净距离的一半中的较小值。
ACI第8.10.3节和第8.10.4节对仅一侧有板的梁和独立T型梁给出了更严格的规定。通常情况下,规则是有效宽度弹性解的保守近似。
许多弹性解被用来估计有效翼缘宽度[5-2],[5-3]。这些解表明,此宽度受荷载类型(均匀、集中)、支承类型、梁间距以及板和梁的相对刚度的影响。但是,必须指出的是,所有的这些研究都忽略了在试验中观察到的翼缘的开裂。
Razaqpur和Ghali[5-4]对钢筋混凝土梁中腹板与翼缘连接的试验进行了综述,提出了两种可用于此类节点加固设计的分析方法。第一种方法是使用第17章介绍的剪切摩擦钢筋,将图5-5a所示的剪应力和法向应力从腹板转移到翼缘上。第二种方法是利用图5-5b所示的支柱和拉杆模型来设计连接。如将在第18-9节所讨论的,需要垂直于腹板翼缘截面的横向钢筋以抵抗横向拉力。如果不提供这种钢筋,梁可能沿着腹板至翼缘内表面的纵截面开裂。图5-5b所示的桁架可作为支柱和拉杆模型。压缩翼缘和张力翼缘的支柱和拉杆模型分别如图所示。第18章的图18-54和图18-55。
第18-9节和第[5-4]节表明,可能需要大量的横向钢筋,尤其是在受拉翼缘中,将力传递到翼缘和翼缘中的纵向钢筋。这种钢筋的布置可以控制翼缘中纵向受拉钢筋的有效性和翼缘宽度的利用程度。
压力在左侧比例的宽度上的扩展图5-5中的翼缘可以通过翼缘平面内的桁架机构理想化。这个桁架由一系列压杆(如图5-5b中虚线所示)和用实线表示的横向拉杆组成。跨中处的一个悬垂于翼缘的合力由K处的力表示。施加在A处翼缘上的水平剪切力通过压杆A-B传递到翼缘中。在B处,支柱A-B中的纵向力传递到支柱B-E中。力的横向分量在支柱A-B中,必须通过横向拉杆B-C等来承受。ACI规范没有给出翼缘中这种横向钢的设计规则。张力翼缘可能需要大量的横向钢。这种钢的布置可以控制翼缘中纵向受拉钢筋的有效性。
施加在翼缘上的荷载会在翼缘与腹板连接处产生负弯矩。如果板是连续的,且跨度垂直于梁,如图5-1所示,或与“梁”垂直,如图5-4所示,则板钢筋恰好足以抵抗这些弯矩。但是,如果板不是连续的(在单独的T型梁中),或者如果板钢筋与梁平行,如图5-4中的“梁”所示,则需要在板顶部配置垂直于梁杆的额外钢筋(ACI第8.10.5节)。这种钢筋的设计是假定翼缘作为一个悬臂,承受系数化的恒载和活载。对于隔离梁,考虑了全悬挑翼缘宽度。对于整体地板系统中的梁(图5-4),本计算中使用有效宽度的悬挑部分。(见第10-6节。)
T型梁分析
一般来说,T型梁的受压区是矩形的,如图5-2b或图c所示。具有此类翼缘的梁可分析为宽度为b的“矩形梁”。如图5-2d所示,在压缩区呈T形的异常情况下,分别考虑了悬挑翼缘提供的阻力和剩余矩形梁提供的阻力。
弯矩承载力的计算遵循第4章中使用的四步程序。
1、假定内部力臂jd。
2、根据弯矩和假定的力臂,计算了产生的压缩力C及其作用线。
3、因为T=C,所以拉力T及其作用线也可以计算出来。
4、然后,弯矩承载力计算:或。
这种分析适用于所有类型的钢筋混凝土梁。
考虑图5-7a所示的梁,应力块深度a应大于翼缘厚度。该梁的内力由受压区质心处的压缩力C(图5-7a阴影区质心)和张力组成,假设钢材屈服,这些形成了一个阻力矩,或。
为了避免需要定位阴影区域的质心(A尚不知道),只考虑两个假设梁的方法是很方便的:
1、梁F,其中下标指的是梁F(图5-7c),其受压区由悬挑翼缘组成,面积,应力为,其中等于0.85,给出的压缩力等于图5-7c中阴影区的0.85。力作用于悬挑翼缘区域的质心。为了平衡,梁F的受拉钢筋面积的选择应使或。这个钢筋的面积是总的一部分,并且选择具有与相同的质心。
2、梁W(图5-7d),其中下标指梁W,该梁是宽度为的矩形梁,具有面积为的
受压区,并利用剩余的受拉钢筋,。该梁中的压力通过其压缩区域的质心作用。该梁的弯矩承载力是受拉钢筋的。
T梁的总抗弯承载力是两个单独梁的抗弯承载力之和,计算
如下:
梁F:
受压区面积=
受压区的力
为了计算梁F所需的钢筋面积,假设,则设,那么
或
力臂为。
将受拉钢筋质心的弯矩求和得出
或者,求出有关作用线的弯矩之和
梁W:
受拉钢筋截面面积
压力
或
力臂是。因此
或
T梁=梁F 梁W。T梁的标称抗弯承载力是梁F和梁W的标称抗弯承载力
之和。因此,
得出
或
最后,计算的力矩承载力为。
有时,a等于。用于计算时可将其视为“矩形梁”。
的确定
在(5-5a和b)的推导过程中,假设。如第4-3节所讨论的,可以通过将计算得出的或比率与或进行比较来检查,由下式得出:
或
其中以psi为单位。如果的单位是MPa,那么在这两个方程中,87000变为600。如果计算出的或比小于(4-19)和(4-20)给出的值,则失效时。
与的比值由(4-20)给出。该方程与截面形状无关,因此适用于T梁。但是,应注意的是,的(4-25)是针对矩形截面推导的,其中压缩区的面积为,需要修改以适用于T截面或宽度随压缩区高度变化的其他截面。
张力控制段和压缩控制段
如第4-3节所述,ACI 318-02第10.3.4节将张力控制截面定义为受拉钢筋最外层的净张力应变等于或超过极限张力应变0.005的截面。因此,如果中性轴深度c与从极限压缩纤维到最远拉伸钢筋层的深度之比小于或等于
这也可以用张力控制极限下矩形应力块的深度a与的比值来表示:
带翼缘受压的T形梁几乎总是张力控制截面。
ACI 318.02第10.3节将压缩控制截面定义为极限拉伸钢(极限压缩纤维中的钢纤维)的净拉伸应变小于拉伸屈服应变的截面。对于60级钢筋,,规范允许但不要求将60级钢筋四舍五入至0.002。对于其他屈服强度,压缩控制限值基于规定的屈服应变,,无四舍五入。净拉伸应变是指由弯曲引起的应变,不包括由预应力、收缩或蠕变引起的应变。
如果大于或等于压缩控制极限时,将发生压缩控制导致失败:
强度折减系数的计算
如果受压区不包含螺旋钢筋,则极端受拉钢()中的净拉伸应变大于或等于压缩控制极限=0.002张力的梁设计用于弯曲,使用=0.65。含螺旋钢筋的压缩控制截面设计采用=0.70。螺旋线用于柱,但很少用于横梁。
在极限受拉钢中,净拉伸应变大于极限受拉极限的梁,其设计值为=0.90。对于受压钢封闭在柱拉杆中的过渡区,在0.0020和0.0050之间,在0.65(极少情况下为0.70)和0.90之间插值。对于60级钢但没有螺旋钢筋的梁,ACI评注第R.9.3.2节给出了
或
因此,由于系数较低,使用超过张力控制极限的钢材强度损失高达28%。
T梁纵筋上限—ACI 318-02第10.3.5节
ACI 318-02第10.3.5节限制了梁中弯曲钢筋的数量,因此净拉伸应变不小于0.0040倍的拉伸应变。名义强度下的拉伸应变。该极限 =0.0040应变,称为梁配筋极限BRL,对应于过渡段。以前的ACI代码限制小于或等于0.75倍的平衡配筋率;因此,。这相当于将极端受拉钢的净拉伸应变限制为0.00376的应变。ACI 318-02第10.3.5节的描述与1999年的ACI规范有所不同,该规范并未限制梁的最大钢筋。然而,这并不是为了修改规范。一直以来,梁的最小延性应与相对应。
T梁配筋上限—ACI 318-02第B.10.3.3节
ACI 318-02第B.10.3.3节中给出了确定最大钢率的替代方法。第4.3节介绍了矩形梁的该程序。由于T型梁使用繁琐,预计将在2005年或2008年从规范中删除,因此不会导出或呈现T型梁。
最小配筋
必须有足够的受拉钢筋,以使开裂后的抗弯承载力大于开裂弯矩。对于翼缘受压的T梁和连续T梁受拉的负弯矩区域,根据ACI第10.5.1节,通过检查是否超过a给出的,
(ACI公式10-3)
式中,和单位为psi,或
式中,和单位为MPa。
当静定T梁(如具有T形横截面的悬臂)的翼缘受拉时,ACI第10.5.2节给出了
式中,和单位为psi,或
式中,和单位为MPa。具有受拉翼缘的静定T梁中的最小配筋量不需要超过(4-34)和(4-34M)给出的值,设为翼缘宽度。
5-3:受压钢筋梁
有时,梁采用受拉刚筋和受压刚筋两种加固方式,本节讨论了受压刚筋对梁性能的影响及其使用的原因,并提出了分析这些梁的方法。
受压刚筋对强度的影响
图5-12比较了有和无受压钢筋的梁在极限荷载下的合力。图5-12b中的梁具有区的受压钢筋,位于距离极端压缩纤维处。两个梁的受拉钢筋面积相同。在两个梁中,总压缩力C=T,其中。在无压钢筋的梁中(图3-12a),这种压力C完全由混凝土抵抗。在另一种情况下,C为混凝土提供的和钢筋提供的之和。由于部分压缩受到受压钢筋的抵抗,将小于C,因此图5-12b中的压缩区的深度小于图5-12a中的。
合成压缩力C的总力矩可得出以下结果:
对于无受压钢筋的梁,
对于有受压钢筋的梁,
式中,是拉力与和的合力之间的距离。
这两个表达式之间的唯一区别是,比稍大,因为比小,因此,对于给定数量的受拉钢筋,加上受压钢筋对可用极限承载力几乎没有影响,从而在无受压钢筋的梁中提供了受拉钢筋屈服。这是插图5-13。对于拉筋的正常比(),弯矩的增加通常小于5%。
受压钢筋的有效性随着远离压缩面而降低。如图5-
全文共6421字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[1643]


