
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
纳米金属的软化
JakobSchioslash;tz,FrancescoD.DiTolla*amp;KarstenW.Jacobsen
丹麦工业大学原子尺度材料物理与物理系中心,丹麦,DK2800 Lyngby
颗粒尺寸在纳米级别的纳米晶固体通常拥有有趣的科学性能,例如硬度和韧性的增强。纳米金属可以通过以多种方式制备,其中最普遍的是高压压缩纳米尺寸颗粒团簇和高能球磨。其结果是晶粒随机排列的多晶金属。通过减小颗粒尺寸,材料的硬度和屈服应力明显增加,这一现象被称为霍尔佩奇效。在此,我们对纳米铜的变形进行了计算机模拟,模拟结果显示,对于最小尺寸的铜,随着晶粒尺寸的增大而软化(霍尔-佩奇效应为3,7)。塑性变形主要是由晶界处原子平面的大量小滑移事件引起的,只有一小部分是由晶粒内的位错活动引起的。因此,我们在小晶粒尺寸下看到的软化是由于原子晶界的较大比例。这种软化最终将限制纳米金属的强度。
为了用计算机模拟纳米金属的行为,我们建立了与实验性的观测到的结构相似的纳米晶样品:本质上,等轴位错冷冻晶粒被窄直线晶粒边界所分隔。每一个样本在10.6纳米的立方体中包括8到64个晶粒,晶粒尺寸在3.3纳米到6.6纳米之间。晶粒通过一个Voronoi产生:一组晶粒中心是被随机选择的,与任何其他中心相比,靠近给定中心的那部分空间被以随机选择的晶体取向的面心立方晶格中的原子填充。一个典型的例子如图所示。为了模拟系统s在大样本中的深度,系统在三个空间方向上无限复制(周期性边界条件)。原子间的作用力是用有效介质理论来计算的,它恰当地描述了金属中的多原子相互作用。用铜来作为进行模拟的金属钯得到了非常相似的结果。在变形系统之前,我们通过在300K下运行50ps的分子动力学模拟对其进行退火,使晶界中的不利构型得以放松。。退火时间延长一倍没有明显效果,温度增加到600K也没有明显效果。
模拟的主要部分是一个缓慢的单轴变形,同时在所有原子坐标下最小化能量。通过在一个方向上扩展模拟单元来应用变形,而尺寸允许在两个垂直方向上变形
总应变为10%的模拟初始和最终构型如图1所示。我们看到晶界变厚了,表明那里发生了明显的变形。在这些颗粒中出现了一些堆积断层。它们是晶粒内位错活动的标志。
为了便于模拟分析,我们通过确定局部晶体的排列顺序来确定哪些原子位于晶界,哪些原子位于晶界内。认为晶粒内部存在局部fc级原子;原子在局部高压(六角形紧密排列)顺序中被分类为堆叠断层。所有其他原子都被认为属于晶界。与传统的颗粒边界所占体积非常小的材料不同,有相当一部分(30%-50%)的原子位于颗粒边界,这与理论估计相符
当变形发生时,我们计算试样的平均应力作为变形量的函数。对于每个晶粒尺寸,我们模拟了7种不同初始形态的变形。图2a为得到的平均变形曲线。我们看到一个杨氏模量约为90 -105GPa的线性弹性区域(随晶粒尺寸增大) , 而非晶态Cu的124 GPa. 这是由于晶界中大量的原子具有较低的杨氏模量。在模拟中可以看到类似的减少,即纳米晶金属从熔融阶段生长16。在弹性区域之后,紧接着的塑性屈服极限大约是1GPa最后,塑性变形饱和,最大的流动压力大约是3 Gpa。理想单晶的理论剪应力约为所用势的6GPa
主要的变形模式如图3b所示,原子的相对运动如图所示。我们看到,大多数变形发生在晶界上,表现为大量的小滑动变形,其中只有少数原子(有时是几十个原子)相对移动。有时,部分位错在晶界处成核并穿过晶粒。这类变形只占总变形的一小部分,但在没有扩散的情况下,当晶粒相互滑动时,需要考虑晶粒的变形。没有位错运动如图3所示,因为当时没有发生模拟。随着晶粒尺寸的减小,更多的原子属于晶界,晶界滑动变得更加容易。随着晶粒尺寸的减小,这导致了材料的软化(图2)。
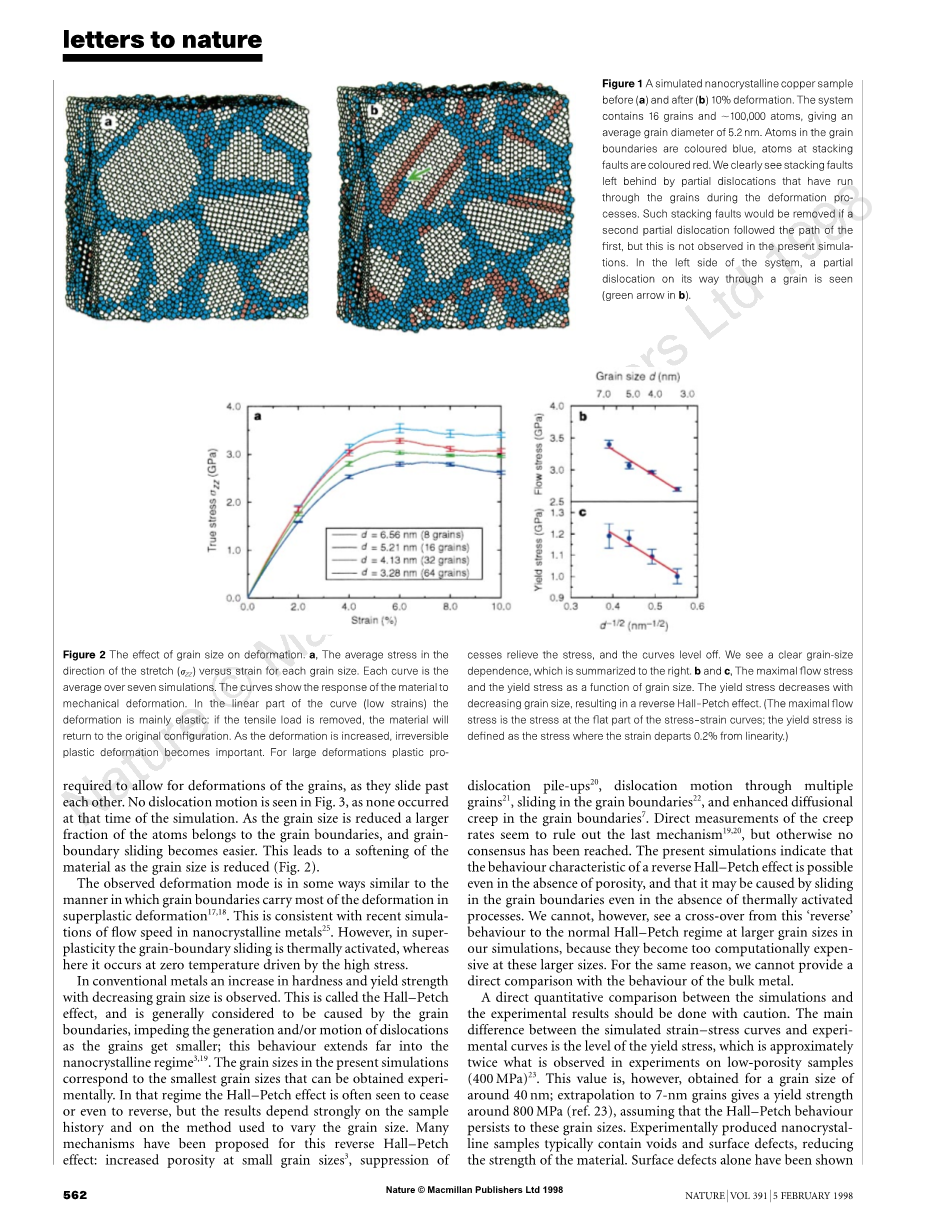
图2晶粒尺寸对变形的影响。 a,拉伸方向上的平均应力与每个晶粒大小的应变之比。每条曲线都是七次模拟的平均值。曲线表示材料对机械变形的响应。在曲线的线性部分(低应变)中,变形主要是弹性的:如果去除拉伸载荷,材料将恢复到原始的结构。随着变形增加,不可逆的塑性变形变得重要。对于大变形,塑性工艺可以减轻应力,使曲线趋于平稳。我们看到明显的对粒子尺度依赖性,总结在右边。b和c,最大流动应力和屈服应力随晶粒尺寸的变化。屈服应力随着晶粒尺寸的减小而减小,导致反向的Hall-Petch效应。(最大流动应力是部分应力 - 应变曲线上的应力;屈服应力定义为应变从线性度偏离0.2%的应力。)
cesses缓解压力,曲线平稳。
我们看到明显的粒度依赖性,总结在右边。
b和c,最大流动应力和屈服应力随晶粒尺寸的变化。
屈服应力随着晶粒尺寸的减小而减小,导致反向的Hall-Petch效应。
(最大流动应力是部分应力 - 应变曲线上的应力;屈服应力定义为应变从线性度偏离0.2%的应力。)
图1(a)和(b)10%变形之前的亚微米晶体样品。该体系含有16个晶粒和100,000个原子,平均晶粒直径为5.2nm。晶界中的原子是蓝色的,堆叠缺陷处的原子是彩色的。我们很清楚地看到了在变形过程中穿过晶粒的部分位错留下的缺陷。如果第二部分位错沿着第一部分的路径移动,则这种堆垛层错将被消除,但是在当前的模拟中没有观察到这种错误。在系统的左侧,可以看到穿过谷物的部分错位(b中的绿色箭头)。
观测到的变形模式在某些方面与超塑性变形中颗粒边界携带大部分变形的方式相似17,18.。这与最近对纳米晶金属流动速度的模拟是一致的25. 然而,在超塑性中,晶粒边界滑动是热激活的,而在这里,它是在零温度下由高应力驱动的。
在常规工艺条件下,随着晶粒尺寸的减小,合金的硬度和屈服强度均有所增加。这被称为霍尔-佩奇效应,一般认为是由晶界引起的,晶界越小,就会阻碍位错的产生和运动;这种行为一直延伸到纳米晶体3,19。模拟得到的晶粒尺寸与实验得到的最小晶粒尺寸一致。在这种情况下,霍尔-佩奇效应经常被认为是停止的,甚至是逆转的,但其结果很大程度上取决于样品的历史和改变晶粒大小的方法。针对这种反向霍尔- Petch效应,人们提出了许多机制:小晶粒孔隙度增大3、位错堆积抑制20、位错通过多晶粒运动21、晶界滑动22、晶界扩散蠕变增强7。对蠕变速率的直接测量似乎排除了最后一种机制19,20,但除此之外,还没有达成共识。目前的模拟结果表明,即使在没有孔隙的情况下,即使在没有热激活过程的情况下,也可能通过在晶界中滑动来实现相反的行为特征。然而,在我们的模拟中,我们不能看到从这种“反向”行为到较大晶粒尺寸的正常Hall-Petch体系的交叉,因为它们在这些较大尺寸下计算成本太高了。出于同样的原因,我们无法直接比较大块金属的行为。
在模拟和实验结果之间进行直接的定量比较时应谨慎。模拟应变应力曲线与实验曲线的主要区别在于屈服应力的大小,大约是低孔隙率试样(400MPa)实验的两倍23。但是,对于40nm左右的晶粒,可以得到这个值;推测7 nm晶粒的屈服强度约为800MPa(参考文献23),假设Hall Petch行为与这些晶粒尺寸一致。实验制备的纳米晶样品通常含有空洞和表面缺陷,降低了材料的强度。表面缺陷本身已被证明能够降低纳米晶态钯的强度至少5倍19,24。
另一个不同是在模拟中缺少热激活过程。这些过程引起了机械性能对应变率的依赖,导致了更高的屈服应力 ,且在激活的过程发生时无论何时都存在。在模拟中没有时间尺度或应变率可以直接定义,但从某种意义上说,过程对应于非常低温的冷却:热激活过程被排除在外,因为工作产生的能量被快速带走。上述蠕变测量19,20结果表明,扩散在变形过程中并不起主要作用。
在后期的模拟变形中,粒子内的平均变形量大于粒子界面的平均变形量(10%-20%),且应力越大,产生的应力越大(见图3c)。这导致了比屈服应力更大的微小流动应力变化(图2b):当晶粒尺寸增大时,最大的流动应力增加,这既是由于晶粒中的应力增加,也是由于原子数在总原子数中所占的比例增大。
M. R. Eskildsen*, P. L. Gammeldagger;, E. D. Isaacsdagger;, C. DetlefsDagger;, K. Mortensen* amp; D. J. Bishopdagger;
*Risoslash; National Laboratory, PO Box 49, DK-4000 Roskilde, Denmark dagger;Bell Laboratories, Lucent Technologies, 700 Mountain Avenue, Murray Hill, New Jersey 07974, USA Dagger;Ames Laboratory and Department of Physics and Astronomy, Iowa State University, Ames, Iowa 50011, USA
低能中子对于材料和磁性结构的分析和表征至关重要。然而,这些中子的连续(基于反应堆)和脉冲(基于散裂)的来源都受到低影响。转向和透镜装置可以显着改善这种情况,因此增加空间分辨率,可检测的样品体积限制甚至可能为中子的构建开辟道路。
Ⅳ.分子动力学方法
Ⅳ.1 牛顿力学
分子动力学方法和蒙特卡罗方法一样,粒子最初是随机分布的。但是,注意颗粒不会碰撞。当然,这一点在蒙特卡罗方法中也必须是这样。在这两种方法中,必须有一个规则来计算整个系统的能量。通常,能量计算为每两个粒子之间的相互作用的总和,因为这使得模型简单。之后,产生新的粒子分布,然后再产生新的粒子分布,最终沿着破坏的顺序发展。该系列称为轨迹。
在蒙特卡罗方法中,每一种新的粒子分布都是随机的, 然后应用一个规则,如Metropolis标准,来决定是否分布可以被接受作为轨迹上的下一个点. 因此,蒙特卡罗方法中没有任何时间坐标,除了分解的序列号。模拟描述了一个处于平衡状态的系统,时间是无关紧要的
在分子动力学方法中,通过使用粒子之间的相互作用,每个新的粒子分布都来自前一个。考虑系统中的一个粒子i,另一个粒子j吸引或排斥它。相互作用取决于粒子i和j的位置,并有助于粒子的总势能
在那个势中粒子受到一个力
它使粒子向某个方向加速。根据牛顿第二定律
这里的明显是粒子的速率. 在分子动力学方法中,在给定时间计算每个粒子的速度v,然后让每个粒子以该速度移动一小段时间,然后重新评估势能,力和速度。
分子动力学方法遵循经典的运动力学,因此是完全确定的。它具有实时坐标,因此轨迹跟随系统的变化及时变化它不仅限于处于平衡状态的系统,而且可用于研究外部扰动下的系统。
Ⅳ.2势能函数
在最简单的例子中,通常使用相同的球形颗粒。粒子之间的相互作用不依赖于方向,只依赖于粒子之间的距离,。使用了几个简单的电势,硬球模型是通过势来求解的。
电势如图所示
lennard-jones势具有这种形式
Ⅳ.5
有时它是以垂直位移的形式给出的
(Ⅳ.6)
前一个功能如图5.2所示,通过对函数作相对于r的微分,很容易求出最小值的位置。事实证明,最低限度在于。该函数在该点具有值(或者在移位电位的情况下为零)。在实际应用中,为了减少计算量,在适当的距离处切断电势,并在该点以外任意设置为零。
如果截止距离足够大,则每对交互的截断误差将是最小的。然而,接近于零的相互作用的数量可能相当大,这可能在总能量中引入一个误差
软球模型使用lennard-jones电位,该电位在最小值处被切断并有位移:
(Ⅳ.7)
电势如图5.3所示
由lennard-jones对电位引起的力为
粒子i受到的总力是
Ⅳ.3分子动力学单位
对lennard-jones电势的检测表明分子动力学方法计算的特殊单位系统是有益的。LJ系统中能量的自然单位是。从而得到无量纲的新能量. 普通单位的能量是
同样,我们选择作为单位, 法向单位的距离表示为
温度的单位是因为热运动的动能是每自由度c,时间的单位是
Ⅳ.4 时间步骤
分子动力学模拟的初始分布与蒙特卡罗模拟的初始分布是一样的,即随机分布。除了一个随机的位置,每个粒子i还被分配一个初始速度v,当=0时粒子初始分布的势能计算为所有对相互作用的和,一旦获得,可以如(Ⅳ,2)所示计算作用在粒子i上的力,这个力引起加速度
它反过来将初始速度v修改为
或者如果一个恒定的力作用了一段时间
现在允许粒子以恒定速度v移动一段时间, 这在时间时为所有粒子产生新的位置, 对于这种新的分布,计算势能rsquo;,力和速度lsquo;rsquo;,然后重复该过程很多次
Ⅳ.5运动方程
在物理学的任何教科书中都可以找到对机械系统经典运动的详细分析. 所有被考虑的系统都是守恒的,系统中的所有力都来自势能函数U. 通过使用3N个独立的广义坐标q和3N 个速度来描述N个粒子的系统. 势能只取决于1位置q. 在迄今为止讨论的简单示例中,使用了无结构球形粒子. 它只能在x y z方向移动. 这种情况下的广义坐标就是笛卡尔坐标. 在实际分子中,键长、键角、扭转角等都是常用的. 在这类系统中,如果不使用振动法向坐标或某些这样的坐标,广义坐标会更加复杂,有时甚至相互依赖.
全文共9527字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[352],资料为PDF文档或Word文档,PDF文档可免费转换为Word


