
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
外文参考文献(译文)
美国和日本采用实用的有限元宏模型
的钢框架结构的抗震模拟
关键词:钢框架结构,地震模拟,有限元方法,倒塌分析,宏观模型,梁壳单元,复合材料的影响
摘要:世界各地的建筑结构都采用了不同的框架设计方法。在日本,被设计的一个用梁连接柱子的3D的地震框架结构双向抗力矩框架结构,在两个方向都有力矩连接,这是一种传统的构造。相比之下,在美国和一些其他多地震地区的国家,单向抗力矩框架模型作在地震框架中由少数昂贵的弯矩连接的分离地震和重力框架结构,被普遍构造。这些不同框架系统的结构在收到大地震的激励下,可能表现出不同的地震反应和倒塌机制。但是,模拟到完全崩溃几乎还没有进行,和这些不同框架系统的安全程度要完全倒塌还无法完全理解。在研究中,美国和日本三层式框架结构的地震模拟使用通用有限元分析程序。实用宏观仿真模型基于梁单元和壳单元。研究发现,在美国和日本的钢框架和位移中,浓度可能发生在相对较小的地面运动水平,最终导致完全崩溃,其中楼板的复合作用加速了柱的屈服。
图二. 日本式结构梁柱节点
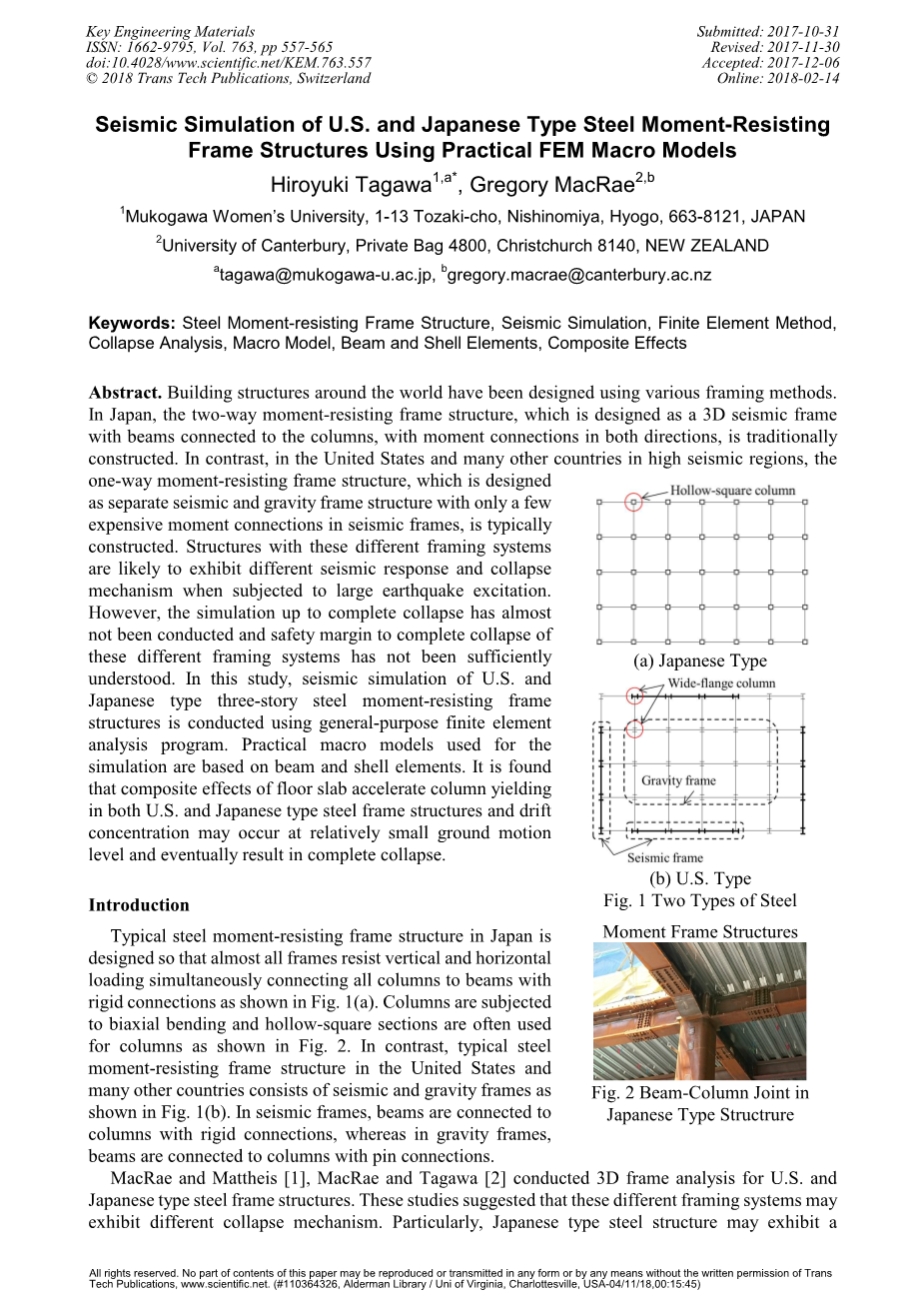
图一.两种钢类型
(a)美国类型
(a)日本类型
介绍:日本的经典钢框架结构设计使几乎所有的框架抵抗垂直和水平荷载同时连接所有柱和梁的刚性连接,如图1(a)所示。柱受到通常采用的双轴弯曲和空心方截面的影响,如图2所示。相反,在美国和其他许多由地震和重力框架组成的国家,典型的钢框架如图1(b)所示。在地震框架中,梁用刚性连接连接到柱上,而在重力坐标系中,坐标系中,梁用销钉连接到柱上。
MacRae and Mattheis 和MacRae and Tagawa 创建了3D模型分析美国和日本的钢框架结构,这些研究认为这些不同的框架结构系统可能表现出不同的坍塌原理。特别是,日本的钢结构可能表现出一种基于双轴柱屈服的软层机理。Hasegawa和Kimura等人创建了对日本和美国钢结构的2D框架分析。Taqawa,MacRae和Lowes在大量分析的基础上,利用这些结构的简化模型创建了基于日本和美国的三层钢耐震框架结构的可靠性分析,但是之前这些研究所用的模型相对简单:(1)纤维梁柱单元和考虑了塑性铰的转动弹簧被利用,(2)楼板不包括在模型中,(3)由于结构分析程序取几何线性假设较小的变形情况,并没有模拟全部破坏行为。最近,由于在计算能力和效率方面的重大进步,详细分析建模结构的大部分都是实心单元来更精确地模拟破坏和倒塌行为得以进行。但是,实体单位建模的计算成本仍是昂贵的,可能不适合目前基于许多仿真的可靠性分析。在这次研究中,对美国和日本三层钢框架抗震模型的地震模拟到完全破坏,在明确考虑了楼板的组合效应后,使用了带有梁柱单元的宏观建模方法。
图三. 采用壳层和MPC结构考虑复合效果
采用梁和壳单元建模方法
本研究中采用了梁壳单元的实用模型进行地震模拟。壳单元是为了考虑楼板的复合作用。梁轴线位于楼板中心线以下的实际钢框架结构的弯矩,然后由于楼板的存在,强度和刚度也增加了。因此,被放置在楼板壳单元和多点约束(MPC)条件下的梁单元被应用于将梁节点与板结点的连接处,如图3所示。MPC条件在假定变形后的剩余平面上,保证了两个节点的距离始终不变。研究采用了通用有限元分析程序LS-DYNA。非线性时程分析法用隐式求解器选项进行分析。几何非线性计算使用了更新的拉格朗日方法。基于退化的各向同性的带有截面积分模型的8结点实体单元的休斯-刘梁单元来进行梁单元计算。基于联合的共旋转和速度应变方法的Belytschko-Lin-Tsay单元来应用于楼板。
综合效果评价
一种梁柱和一种梁-柱-板组件,如图4所示,分析了4种复合材料对楼板性能的影响。梁是W18*35(sigma;y=248 N/mm2),柱是W14*82(sigma;y=325 MPa),混凝土板的 厚度是150mm。假定混凝土是弹性的或者是屈服强度为25 N/mm2的完美弹塑性材料(EPP)。梁用刚性连接或销连接到柱上。侧向力和梁转动角theta;b关于组装的梁柱和梁柱板的关系在图5中相比较。同时,在梁柱板组件的模型中,节点处梁的力矩需求Sigma;Mbeam和节点上下柱的弯矩之和 Sigma;Mcolumn在图6中作刚性连接比较,图7中作销连接比较。根据楼板的存在,Sigma;Mcolumn变得比 Sigma;Mbeam更大。101/5000 复合效应产生的弯矩近似等于程序中计算和输出的梁节点处轴向力N乘以梁的中心线与楼板之间的距离。这添加到Sigma;Mbeam和图6和图7所示。 Sigma;Mcolumn 相似,明显的不同是由于d的近似值。如果混凝土材料开裂或屈服,对柱的弯矩要求可能是有限的。当混凝土材料为EPP的情况如图5的虚线所示。研究发现,假定混凝土材料为弹性材料,增加了柱的弯矩需求。
图四. 测试元件的复合效果
分析了钢框架结构的抗震性能和地震记录
日本和美国钢框架结构的分析模型如图8所示。构件大小列表在表1中给出。在日文类型中,采用空心方截面柱。钢的弹性模量为205 kN/mm2,混凝土的弹性模量为11.25 kN/mm2。钢的密度为7.85吨/立方米,混凝土的密度为2.4吨/立方米。楼板的厚度是150mm。构件和截面尺寸对于美国类型,参照SAC steel项目设计的三层钢框架结构,对于日本类型,参照Hasegawa等人按日本标准设计的三层钢框架结构。同时,对以往研究中采用统一建筑规范(UBC)设计的日本式进行了分析。这些结构分别称为美国型(SAC)、日本型(BRI)、日本型(UBC)结构。根据相邻梁的划分,将柱、梁的各梁单元划分为8个,将楼板的每条边划分为8个。在美国重力框架结构中,梁的模型是用销钉连接柱。将米塞斯屈服面、各向同性和运动硬化模型与3%应变硬化相结合应用于钢的本构关系。对于美国型、日本型(BRI)和日本型(UBC)结构,单向计算典型梁柱节点的柱/梁强度比分别为2.02、2.28和1.38。
第1、2、3个自然周期如表2所示。由于美国框架中地震框架的数量较少,美国地震框架的第1和第2自然周期(对应于平移模式)要大于日本地震框架。而第三个自然周期对应于扭转模态,由于刚性地震框架的位置在结构的周向,所以与日本地震模式相似或小于日本地震模式。这些自然周期比以前的研究得到的要小。这是因为(1)研究模型通过对楼板进行建模,考虑了组合效应;(2)厚度为0.15 m的混凝土楼板与钢构件的总质量结果,小于以往研究中基于恒荷载和活荷载计算的结果。
从SAC记录套件中选择了两组地震记录来分析结构。LA0506记录集由LA05和LA06的设计等级记录组成,其震级是根据洛杉矶50年内超过10%的概率事件确定的。近断层(NF)记录集NF1718由1995年神户地震的更严重记录组成。本研究考虑了45度的顶升角[1,2]。
设计水平地震动的地震响应LA0506
图9比较了三种钢框架结构在设计水平地面运动LA0506(45°)作用下的X、Y向1层位移角(SDA)。美国型、日本型(BRI)和日本型(UBC)的最大1级SDA分别为X方向1.2%、0.44%、0.92%,Y方向0.94%、0.58%、0.63%。第1、2、3阶SDAs在X、Y方向上的相互作用如图10所示。在这些图中,通过将独立的X或Y方向振动的X和Y方向的位移响应结合起来,得到了100%组合规则[1,2]的包络线。结果表明,三种结构的三维位移响应总体上都在设计水平地震动的100%组合规律之内。因此,三维响应可以通过结合二维响应来理解X方向和y方向的振动。对于美国型号(SAC),第一SDA大于第二和第三SDAs。而日本型(BRI)中,第2个SDA大于或类似于第1和第3个SDA。
近断层地震动的地震响应NF1718
图11中比较了三种结构在近断层地震动NF1718(45°)作用下的X、Y方向的一阶SDAs。美国型、日本型(BRI)和日本型(UBC)的最大1级SDA分别为7.0%、2.3%、6.9%、3.8%、1.8%、4.3%。在美国型和日本型(UBC)中也观察到较大的残余漂移。第1、2、3阶SDAs在X、Y方向上的相互作用如图12所示。在美国型和日本型(UBC)中,第1个SDA明显大于第2和第3个SDAs,这可能是由于软层机制。相比之下,日本型(BRI)的1级和2级SDAs是相似的。然而,有趣的是,3D漂移响应在U.S.类型的100%组合规则内。
增量动力分析
为了了解地震反应、屈服和倒塌机理的发展,进行了增量动力分析(IDA)。NF1718(45°)的强度从0.2倍缩放到2.0倍。三种结构在两个方向上的最大SDAs如图13所示。顶板漂移角(RDA)为顶板最大位移除以总高度,漂移集中系数(DCF)为顶板最大位移除以RDA,如式所示
图14所示。从图14(b)可以看出,美国型和日本型(UBC)的DCF较大。先前的研究[1,2],不包括楼板的组合效应,表明大漂移浓度不可能发生美国类型(SAC)由于大柱/梁强度比率计算一个方向和重力列,不接受从相邻时刻输入光束通过销连接。柱弯矩相互作用如图15和图16所示,分别为美国型地震柱和重力柱,日本型结构内部柱弯矩相互作用如图17所示。在这些图中,给出了考虑重力作用下轴向力的屈服面。结果表明,在美国型结构中,地震柱的屈服系数为0.4,重力柱的屈服系数为0.8。在美国型框架的一层梁柱节点的梁力矩要求Sigma;Mbeam和柱力矩要求Sigma;Mcolumn进行了比较,如图18所示。
Sigma;Mcolumn是Sigma;Mbeam 1.46倍。Sigma;Mcolumn 和 Sigma;Mbeam 的不同是由楼板和梁的轴向力所产生的力矩,等于N*d。同时,Sigma;Mbeam是1.21倍梁塑性弯矩能力的总和,Sigma;Mp,梁。
因此,根据3404年国际(2007)[15]和文献[16],这可以等于仅由板效应引起的超强度系数phi;oss,是1.46,phi;oms裸钢的人员超编的因素,是1.21。复合效应加速了柱的屈服,并可能导致漂移浓度。
坍塌模拟
如图19所示,美国型(SAC)和日本型(UBC)结构分别在规模系数为1.6和1.8时完全倒塌。如图19(a)所示,在美国型钢框架结构中,随重力框架薄弱区域的起始点出现倒塌现象,这可能是由于楼板的复合作用导致柱屈服的结果。
结论
采用考虑楼板组合效应的梁壳单元宏观建模方法,对三层美日两国钢框架结构进行了抗震模拟。楼板的复合作用在两种结构中都可能加速柱的屈服,在较小的地面运动水平上均可能发生位移集中,最终导致完全倒塌。
现在
这项工作由编号26420575和编号17K06661的jsp KAKENHI赠款支持。
相关文献
- G. MacRae, J. Mattheis, Three-dimensional steel building response to near-fault motion, Journal of Structural Engineering ASCE 126(1) (2000) 117-126.
- G. MacRae, H. Tagawa, Seismic behavior of 3D steel moment frame with biaxial columns, Journal of Structural Engineering ASCE 127(5) (2001) 490-497.
- T. Hasegawa, K. Takahashi, M. Seki, T. Nagao, H. Mukai, K. Fukuda, Comparison between seismic performance of U.S. steel perimeter and Japanese spatial moment resisting frames, AIJ annual meeting (1998) 903-908.
- Y. Kimura, Effect of elastic columns on drift concentration for Japan and US steel structures, AIJ annual meeting (2007) 1023-1024.
- H. Tagawa, G. MacRae, L. Lowes, Probabilistic evaluation of seismic performance of 3-story 3D one- and two-way steel moment-frame structures, Earthquake Engineering and Structural Dynamics Vol. 37 Issue 5 (2008) 681-696.
- T. Miyamura, T. Yamashita, H. Akiba, M. Ohsaki, Dynamic FE simulation of four-story steel frame modeled by solid elements and its validation using results of full-scale shake-table test, Earthquake Engineering and Structural Dynamics Vol. 44 Issue 9 (2015) 1449-1469.
-
H. Tagawa, T. Miyamura, T. Yamashita, M. Kohiyama,
全文共7368字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[451660],资料为PDF文档或Word文档,PDF文档可免费转换为Word


