超弹性Cu-Al-Mn-Ni微柱的取向依赖性
J. Fornell a, b, *, N. Tuncer a, C.A. Schuh a
a麻省理工学院材料科学与工程系,剑桥,马萨诸塞州02139,美国
b西班牙贝拉特拉,08193巴塞罗那自治大学DeFiacute;sica
文章信息
文章历史:
2016年7月11日收到修改后,2016年10月5日收到
2016年10月10日接受后,2016年10月13日在线提供
关键词:
Cu-Al-Ni-Mn形状记忆合金
超弹性各向异性
微柱
微压缩测试
马氏体相变
摘要
研究了压缩下单晶Cu-Al-Mn-Ni形状记忆合金微柱的超弹性行为与晶体取向的关系。 直径约2微米的柱状柱体是由目标晶体方向微加工而成的。 虽然靠近[001]方向取向的柱子表现出最大的总相变应变(〜7%),但由于塑性变形具有较高的弹性各向异性以及较大的应力,因此在靠近[111]方向铣削的柱子中,压缩响应占主导地位 需要诱导转化。 为gamma;#39;和beta;#39;马氏体构造了形状应变轮廓图,并且使用Clausius-Clapeyron方程计算了马氏体开始应力。 在实验和计算结果中都观察到相同的一般趋势,但有一些例外:在微米柱中观察到较大的转变应力和较低的转变应变。
copy;2016 Elsevier B.V.保留所有权利
1.介绍
形状记忆效应依赖于马氏体相变:从高对称性的高温相到低对称性的相的一阶无扩散固—固相转变,其在较低温度下是稳定的。这种转变可以被热或机械激活,并且取决于在测试温度下哪个相是稳定的,形状记忆合金(SMA)可以表现出超弹性或形状记忆效应。
Cu基形状记忆合金过去几十年来已经被广泛研究,因为与其它形状记忆合金(例如NiTi,AuCd,Pt合金等)相比,它们具有优异的热机械响应以及较低的材料成本。通过降低beta;相中的有序度,已经向Cu-Al合金添加了beta;稳定剂元素,例如Ni和Mn,以增加它们的延展性;因此,在三元和四元Cu基合金中改善其形状记忆性能已经被报道了[1,2]。尤其是,块体Cu-Al-Ni和Cu-Zn-Al合金在压缩和拉伸中的力学行为已被广泛研究。有利的取向单晶Cu-Al-Ni形状记忆合金表现出高达10%张力的可恢复应变[3]。然而,块状多晶铜基SMAs在马氏体相变过程中是脆性的,易于沿晶断裂,部分原因是它们的弹性各向异性较大[4,5]。例如,沿[111]方向引起马氏体相变所需的应力是沿CuAlNi合金[001]方向所需的应力的两倍,并且这两个方向的总应变分别大约为4和10 %[6]。这种取向依赖性对加载方式也是敏感的,即沿同一轴拉伸与压缩导致不同的转变应变[7-9]。
纳米和微米尺度的Cu基形状记忆合金(SMAs)在过去几年引起了人们的关注,因为它们有可能在微机电系统(MEMS)中用作微米和纳米尺度的致动器[10-20]。已经在Cu-Al-Ni微纳米柱[15-18]中发现了优异的超弹性行为,这种行为能够在至少数百个循环内进行静止循环[16,18]。然而,形状记忆合金在微观和纳米尺度上的研究并不简单,一些测量的行为与名义上类似的散装材料中观察到的行为有所不同。例如,在Ni基形状记忆合金中,当样品长度缩短时,通常观察到较低的转变应变和较大的马氏体转变应力。在NiTi [10,14,19]和Ni-Fe(Mn)-Ga微柱[13,21,22]中研究了这种尺寸效应。在Cu基形状记忆合金中,San Juan及其同事[20]观察到三种不同的尺寸效应:随着样品尺寸的减小,他们注意到(i)马氏体转变的临界应力增加,(ii)奥氏体逆转,以及(iii)马氏体变体选择规则的明显变化。
上述两个关键问题,即样品尺寸效应和晶体取向效应,很少被一起研究,而据我们所知,迄今为止这种结合只在NiTi 形状记忆合金中被采用[10,12,19]。我们并没有意识到对Cu基微柱中转变应力和应变的取向依赖性进行系统的研究。因此,这项工作的目的是对这个问题进行第一次研究。
2.理论计算
Cu-Al-(Ni)-(Mn)合金由其立方beta;相(DO3或L21型有序结构)转变为斜方晶系相(2H堆叠结构)或单斜相(M18R,M9R或6M1堆叠结构)当冷却到低于马氏体结束温度Mf时,或当小于施加的外部应力[1,2,23,24]时。虽然M18R和M9R是文献中用于描述转化的最广泛的堆叠结构,但有几篇论文认为6M1晶胞是实际形成的并更准确地反映了产物相对称性的单元[24-26],因此这是目前工作中考虑的单斜相。
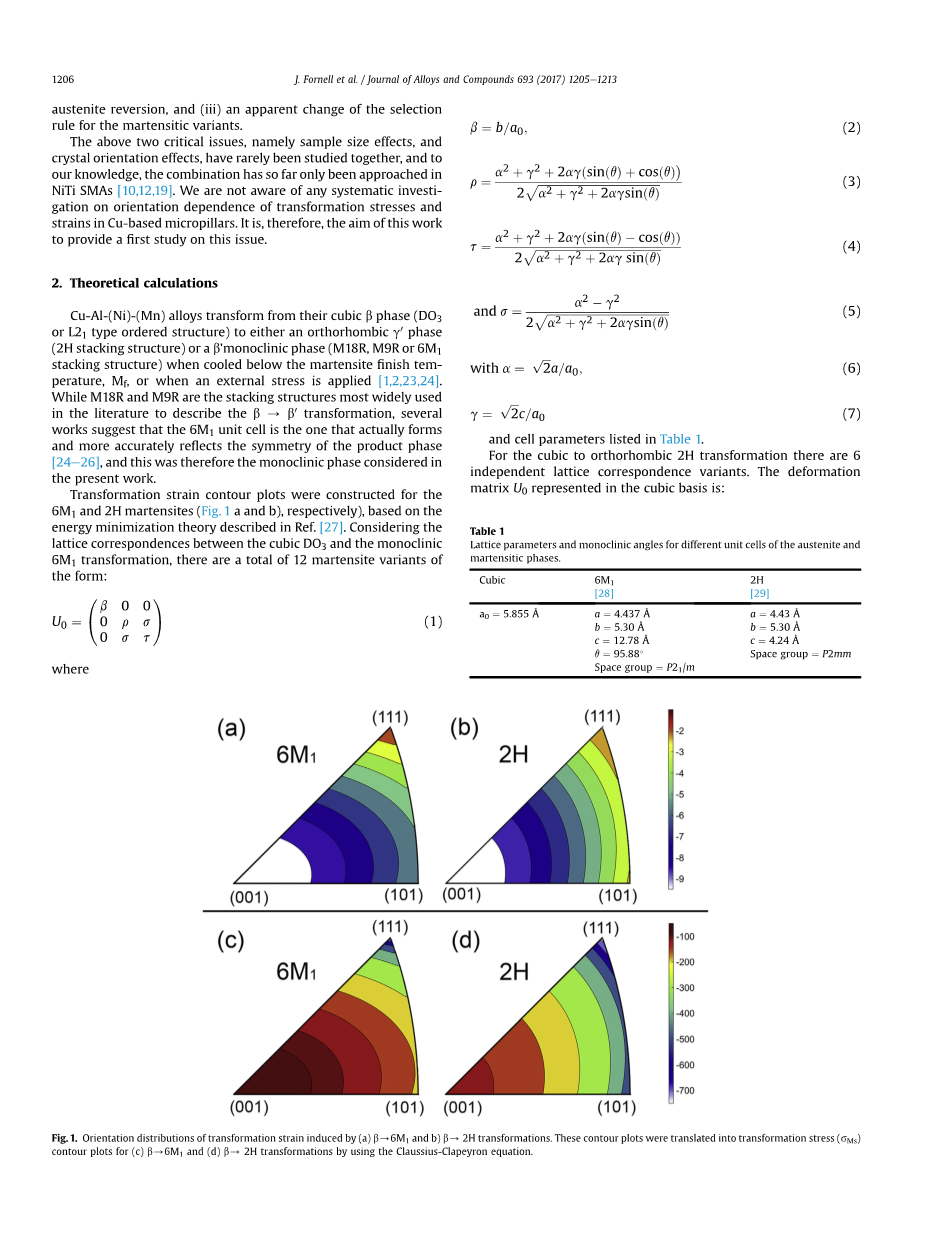
基于参考文献中描述的能量最小化理论,分别针对6M1和2H马氏体(图1a和b)构建了转变应变等高线图 [27]。考虑到立方DO3和单斜6M1转变之间的晶格对应关系,总共有12种形式的马氏体变体:
和表1中列出的电池参数。
对于立方到正交2H转换,有6个独立的晶格对应变体。 以立方为单位表示的变形矩阵U0为:
表1
奥氏体相和马氏体相不同晶胞的晶格参数和单斜角。
其中a,b和g是如上所定义的变形拉伸,并且2H马氏体的晶胞参数在表1中定义。
图1.(a)b / 6M1和b)b / 2H转化诱导的转化菌株的方向分布。 利用Claussius-Clapeyron方程将这些等值线图转化为(c)b / 6M1和(d)b / 2H变换的变形应力()等值线图。
使用Bain变换矩阵(U0)并应用相应的旋转(R)以获得其他马氏体变体,在方向be上的相变应变εtr被计算为:
在一定方向εtr的值是压缩的最大可恢复应变,对应于形成最有利的马氏体变体[5,26]。从图1(a)和图2(b)的轮廓应变图可以看出,在压应力下,在(001)极附近总是可以观察到较大的εtr,最靠近(111)其中马氏体相形成。两者之间的差别通常是微妙的,在(101)极附近是最明显的。
基于上述理论转变应变,引发马氏体相变的理论单轴应力,使用Clausius-Clapeyron方程计算,其中,变换DS的熵变为2H,6M1马氏体分别取1.54和1.11 J / mol C [30],合金元素的组分加权平均摩尔体积为V = 7.79 cm3 / mol。计算中使用的试验温度和马氏体开始温度Ms分别为18℃和36℃。计算的6M1和2H马氏体的等值线图如图1c和d所示。
虽然弹性各向异性已被量化的铜基形状记忆合金 [26,31,32],在这项工作中使用的组成是相对较少的研究,没有列表弹性常数在文献中被发现。相反,我们使用密切相关的Cu67的弹性常数。由Prasetyo等人提出的5Al25Mn7.5合金 [33]。该材料在DO3阶段的弹性各向异性参数为A = 2C44 /(C11-C12)= 10.9,其中C11 = 135,C12 = 118,C44 = 92.5GPa。
3.合金和实验方法
通过在密封石英管中在氩气气氛下熔化高纯度(99.9wt%)元素粉末制备具有组成Cu-23.2Al-3Ni-4.6Mn(原子%)的母合金。具有〜200mm直径和几米长的圆形横截面的导丝通过使用旋转滚筒丝网连铸机(PSI)从约1300℃的熔体温度熔融喷射到装满水325rpm的旋转鼓上, Ltd. England)在其他地方描述[34]。为了促进b相的形成,在氩气气氛下,在800℃退火3小时并水淬火。用差示扫描量热法(DSC)以10 K / min的速度确定转变温度(图2),Afasymp;- 20 ℃,As asymp;-41℃,Msasymp;- 36℃和Mf asymp;-55 ℃(奥氏体完成和开始和马氏体开始和结束,分别)。如通过DSC测量所证明的,合金在室温下是奥氏体的,并且因此在压缩期间可以预期超弹性行为。通过X射线衍射(未示出)获得了单相微观结构的进一步证据,其中观察到的所有峰均属于奥氏体beta;相。
图2.加热和冷却过程中的吸热和释放,分别通过示出转变温度的DSC扫描显示。
将导线切成约3厘米长,埋入导电树脂中,并通过一系列较细的研磨物研磨并抛光,使用0.05毫米胶体二氧化硅进行最后一步的镜像样外观。在FEI XL-30扫描电子显微镜(SEM)上通过电子背散射衍射(EBSD)测定晶粒取向。图3a是直径范围从180到200mm的电线的SEM图像。相应的EBSD数据如图3b所示。可以观察到大小在100至400毫米的不同方向的谷物,并且可以从每个谷物中研磨各种微柱。使用Helios Nanolab 600双光束聚焦离子束(FIB)铣削系统在30kV加速电压下以9.3至28pA的电流进行圆柱形微压缩样品的微加工。在支柱周围研磨直径为40毫米的沟槽,深度为〜2毫米,为微机械测试提供间隙。圆柱形柱子的直径从1.4到2.2毫米不等,我们没有观察到明显的尺寸效应。例如,对于单一的方向,比较直径1.6和2.1毫米的柱子,我们分别测量了151和153兆帕的变形应力,应变分别为3.96和3.64%。我们得出结论:在这里测试的样本量的狭窄范围内,我们的数据点之间的尺寸效应可以忽略为一阶。纵横比保持在2和3之间。在这个范围内,支柱纵横比的影响与参考文献一致可以忽略不计。 [35,36]。
图3. a)Cu-Al-Mn-Ni线的扫描电子显微镜(SEM)图像。 b)相应的EBSD图像(插图:反极图定向图例,显示晶体方向参照加载轴)。
在Hysitron Triboindenter上,在开环负荷控制下,以250mN / s的加载速率使用20mm直径的圆锥形顶端,在18℃(高于Delta;F〜38℃)下进行微压缩试验,随后以相同的速度卸货。这个过程在给定的支柱上重复多次,增加每个循环的最大程序负荷(Pmax),直到发生故障。每隔一个周期后,通过扫描接触式pro-filometer模式的表面来检查尖端定位,以解决任何可能的样品漂移;必要时尖端重新贴在柱子上。为了进行比较,使用平均直径和立柱高度的变化将载荷 - 位移数据转换成应力 - 应变数据。为了尽量减少由锥形锥体产生的应力 - 应变计算误差,使用柱体高度一半的直径代替柱体顶部的直径,但应该牢记的是,这些真实的应力状态支柱不完全统一,这是讨论中的不确定性的来源。
图4a显示了单个柱子的典型超弹性响应曲线。为了实验确定最大转变应变(εmax)和诱导每个支柱马氏体转变()所需的应力,我们在增加的应力水平下系统地进行了探测。通过检查系列并确定在卸载之后存在显着的永久变形的施加载荷水平来确定最大变形应变。图4b显示了一个典型支柱的一系列数据,其中增加载荷系列导致总应变增加,在卸载达到一定载荷水平(即超弹性)之后基本没有残余应变。当总应变达到6%左右时,永久变形程度急剧增加,表明施加的荷载已经耗尽了可采的变形应变,并开始产生柱。选择具有最小永久应变的总应变最高的循环(例如图4b中箭头所示的测试)以分配最大的变形应变。对于相同的循环,如图4a所示记录马氏体相变的临界应力,如曲线的线性弹性和转变平台部分上的切线结构所示评估的。使用类似的结构来评估所有的临界应力,如马氏体结束,奥氏体开始和结束所示。在下文中,除非另有说明,否则我们将讨论局限于这些曲线,即那些只消耗完全可用的变换应变而不会引起太多塑性的曲线。
图4. a)支柱p8.9的代表性应力 - 应变曲线。 b)在柱子p8.9上进行的循环中总应变的永久应变的演变。 阴影圆圈(标有箭头)表明,在临界总应变应变以上,永久应变开始快速增加。 这是选择代表这种取向的周期,这被认为是耗尽了完全可以实现的转变应变。20℃时的应变率。
为了比较,使用动态机械分析仪(DMA,TA Instruments Q800)测量截面直径为〜180mm和7.8mm长度的铸态多晶丝另一段的超弹性响应。 DMA测量是通过在20℃下施加3times;10 4 s -1应变率的单轴拉伸力来进行的。
4.实验结果
图5a显示了所有在这项工作中实验测试的立柱,显示加载前(在奥氏体中)柱轴取向的立体三角形。方位用“p”标记,后跟[001]和支柱轴之间的角度(以度为单位)。支柱也用颜色标记,[111] [101]和[001]分别设置蓝色,绿色和红色的色标。一些选定的晶粒取向的有代表性的应力 - 应变曲线如图5b所示。不同的机械响应根据方向立即观察到:加载曲线的初始线弹性部分的不同斜率,不同的变形应变和诱导转变所需的不同应力。在靠近[001]极点的柱体中获得较大的转变应变和较低的反式应力,而在[111]较接近的那些柱体在较大的转化应力下则表现出较小的反式应变。例如,引起马氏体转变的临界应力,对于一个接近[001]的定向柱,只有〜130 MPa,总可恢复应变大于7%。相反,对于接近[101]的取向,几乎为400 MPa,总应变只有〜2.5%。
图5. a)立体三角形表明在这项研究中测试的支柱轴的方向。 b)a)中一些支柱取向的微压缩测试结果。
为了突出主要取向性质的一些差异,在图6中进一步检查了
全文共13708字,剩余内容已隐藏,支付完成后下载完整资料

英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[17109],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


