
英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
冲蚀磨损
摘 要
因输送固体颗粒而造成的材料表面冲蚀,无论在世界何处都是一个尚未解决的工业难题。相关文献中,有关于弯头侵蚀数据非常有限。几乎所有可用的数据都是关于弯头拱背部分的,或者是有关于表面材料质量损失的,并没有与管道弯头冲蚀分布相关的数据。在一则报道文献中,作者使用表面轮廓仪进行测量,提供了标准弯头(90°弯曲,弯曲半径与管道直径比等于1.5)的冲蚀深度的详细表面图,他在40times;20的网格中,报告了200公斤和300公斤砂子通过弯头时引起的管道冲蚀情况。其中沙粒的平均直径为184mu;m,这些砂粒在空气的驱使下在管道内移动,空气的流动速度为80m/s,温度为室内温度。
然后使用传统的欧拉-拉格朗日方法对管道进行冲蚀数值模拟,得到管道弯头部分的冲蚀分布。我们发现,在使用这种方法时,需要假设粒子是与光滑的管道壁面碰撞,这样做会导致无法准确预测管道的最大侵蚀深度,并且特征性“V形”形侵蚀疤痕不会再模拟数据中体现出来。通过采用合适的粗糙管道壁面碰撞模型,可以更准确地预测侵蚀深度和冲蚀分布。除此之外,颗粒形状、表面轮廓和表面粗糙度都是可能影响到冲蚀行为的因素。
数值模拟表明,如果要得到准确的冲蚀分布预测,将粒子与粗糙壁面之间的碰撞以及其他更复杂的流动行为纳入数值模拟中是有必要的。
1.介绍
弯管或管道弯头在许多工程过程中都会被使用到。当颗粒通过这些弯曲的输送管道会引起对壁面材料的冲蚀磨损,从而导致需要经常性的更换昂贵的部件或是部件故障。在石油和天然气工业中,从井眼中产生的砂子以高压和高速的状态通过地面上的管道,容易造成重大安全隐患。这样的问题在氧化铝工业中同样有可能会发生,因此炼油厂的弯管必须定期更换以避免因腐蚀性泥浆而造成的高压泄漏。以上这些只是无数依靠管道完整性,来安全可靠地输送颗粒材料的工业过程中的其中两个。
图1a显示了一个标准的90°弯头。构成弯头的管道的直径等于D,而弯头本身的半径表示为r。处于最小内表面的弯曲半径称为内弯曲面,其半径等于r内。同理,处于最大内表面的弯曲半径称为弧度,其半径等于r外。周围与弯头之间的距离定义为theta;。并且流体从入口处的theta;= 0°的地方流至出口处,theta;= 90°的地方。这些量在图1a中都被表示了出来。
几十年来,人们一直都在研究当颗粒通过管道弯头时的冲蚀磨损行为。一些最早的工作是由Bikbaev等人完成的[1],他们做了一些关于使用空气作为沙粒的载体,输送通过90°弯头的研究。虽然没有提供实验装置的相关信息,但似乎使用轮廓测量装置来确定在不同量的沙子通过弯曲部分之后沿着外倾角的材料厚度。显示了弯头周围位置所受冲蚀磨损随时间的变化(单位为mm/h),根据Bikbaev等人使用的弯头,他们将最大侵蚀点定位在theta;= 25°和theta;=35°之间。工作中还显示了颗粒在通过弯头时浓度分布的图像。他们的图像显示了砂粒在对壁面造成的侵蚀区域分布,并且这种分布行为将会像显示的那样,对于当前的工作是有意义的。
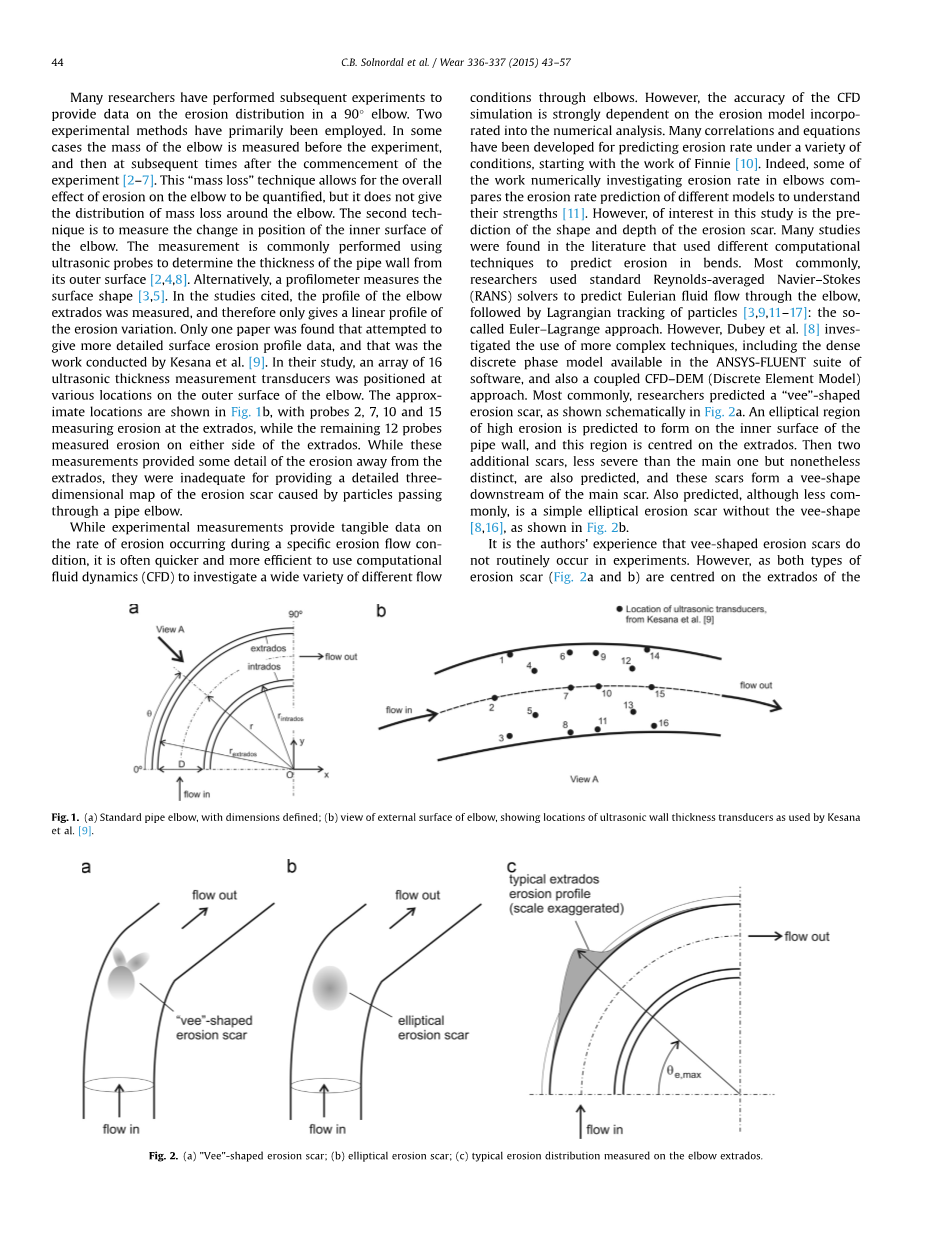
图1.(a)标准管弯头,尺寸已定义; (b)肘部外表面的视图,显示了Kesana等人使用的超声波壁厚换能器的位置[9]
图2.(a)“V形”侵蚀疤痕; (b)椭圆形冲蚀疤痕; (c)弯头拱背测量的典型侵蚀分布
许多研究人员进行了后续的实验工作,以提供有关90°弯头侵蚀分布的数据,主要采用了两种实验方法。在某些情况下,在实验前测量弯头的质量,然后在实验开始后的后续时间内继续测量弯头的质量[2-7]。这种“质量损失”技术可以对弯头的侵蚀整体影响进行量化,但不能给出弯头周围质量损失的分布。第二项技术是测量弯头内表面位置的变化。通常使用超声波探头测量管壁外表面的厚度[2,4,8]。或者,轮廓测量仪测量表面形状[3,5]。在所引用的研究中,测量了弯头外倾角的剖面,因此只给出了侵蚀变化的线性分布。只有一篇论文试图给出更详细的地表侵蚀剖面数据,这是由Kesana等人所做的工作[9]。在他们的研究中,将一组16个超声波测厚传感器放置于弯头外表面的不同位置。图1b显示了大致的位置,其中探针2,7,10和15测量了拱背处的侵蚀,而其余12个探针测量了拱背两侧的侵蚀。虽然这些测量结果提供了一些关于拱背部位侵蚀的细节,但它们不足以得到因颗粒通过管道弯头而引起的侵蚀疤痕的详细三维图。
尽管实验测量提供了关于在特定冲蚀流动条件下发生的侵蚀速率实际数据,但使用计算流体动力学(CFD)通过弯头调查各种不同流动条件下的管道,通常更快且更有效。然而,CFD模拟的准确性十分依赖于纳入数值分析的侵蚀模型。从Finnie的工作开始,已经开发了许多相关方程来预测各种条件下的弯头冲蚀速率[10]。事实上,一些利用数值模拟方法研究弯头侵蚀速率的工作,比较了不同模型下的管道弯头侵蚀速率预测,以了解它们各自拥有什么优点[11]。然而,对这项研究感兴趣的部分主要是侵蚀疤痕的形状和深度的分布。在文献中发现了许多使用不同计算技术来预测弯头侵蚀的研究。通常,研究人员使用标准雷诺平均Navier-Stokes(RANS)求解器来预测欧拉流体通过弯头的流动,然后用拉格朗日公式计算跟踪粒子[3,9,11-17]:这就是所谓的欧拉-拉格朗日方法。但是,Dubey等人[8]研究了使用更复杂的技术,包括ANSYS-FLUENT软件套件中的密集离散相模型,以及耦合CFD-DEM(离散单元模型)方法。研究人员预测了一种最常见的“V形”腐蚀疤痕,如图2a所示。预计在管壁的内表面上形成高度侵蚀的椭圆形区域,并且该区域集中在拱背外侧。然后再预测两个额外的疤痕,比主要疤痕严重但仍然不同,并且这些疤痕在主疤痕的下游形成V形。如图2b所示。尽管不太常见,我们也可以预测简单的没有“V形”腐蚀疤痕的椭圆形侵蚀疤痕[8,16]。
作者本人的经验是,“V形”腐蚀疤痕在实验中并不经常发生。然而,由于这两种类型的侵蚀疤痕(图2a和b)都集中在弯头的外倾角上,所有仅限于外倾角测量的实验数据都不会提取验证CFD框架中的侵蚀模型所需的详细程度。 虽然Kesana等人的工作[9]确定了一些外倾角侵蚀测量,从图1b可以清楚地看出,测量的数量和位置并不足以辨别许多已发表的CFD软件中的冲蚀预测模型。
人们承认,工程师通常只会考虑最大侵蚀点处的位置和侵蚀速率,这通常会在弯头的外壁处发生。但是,在很多情况下,在几何结构更复杂的情况下(例如阀门或其他配件)会发生侵蚀。为了可靠地预测这些复杂几何形状中的最大侵蚀点,模型必须首先能够以比较简单的几何形状(如弯头)准确预测材料的侵蚀分布。
根据对已出版工作的审查,发现了一个非常详细的侵蚀实验数据集,描述了通过90°弯管输送气流所产生的侵蚀疤痕,这对文献有重大贡献。本文第2-4节提供了实验设备的详细信息,用于创建此类数据集的技术以及实验条件,而第5部分提供了图形和数字的数据。在第6节中提供了关于这种侵蚀的典型欧拉-拉格朗日CFD计算的更多细节,并且研究了预测的V形腐蚀疤痕的原因。然后在第7节中讨论了文献中已经公布的结果的缺点,最后在第8节中得出结论。
2.仪器
2.1坐标测量机
为了得到产生在90°弯管中发生的侵蚀磨损的详细的三维表面图,使用谢菲尔德Dis-covery II D-8坐标测量机(CMM)。 坐标测量机是一种能够绘制三维表面轮廓的轮廓测量仪。 它包括可以使坐标测量机安装在测量表面的平台,以及一个可以任意放置在两个水平尺寸(x,y)上的计算机控制的探针头。 然后探头下降到测量表面上,并确定表面在该x,y位置的垂直位置(z),给出表面的完整三维图。 Graham等人先前提供了选择这种设备的细节[18]。坐标测量机测量的总体精度为76mu;m,由71mu;m的测量不确定度和75mu;m的估计位置不确定度组成[19]。
2.2流量隧道
图3.(a)实验前肘部内表面的照片; (b)两个肘侧合在一起的示意图; (c)用螺栓连接在一起时。
实验中使用的流量隧道在图4中以图的方式示出,具有详细的尺寸。它是主要测试部分直径等于102.5毫米的开路隧道。空气从75千瓦的风机进入隧道,进入距地板附近200毫米的水平管道。在两个90°弯头和一个减速器交汇之前,砂子以恒定速率进入该管道,然后进入垂直管道。垂直管道的直线部分长度等于25.8D,并在实验管道弯头处结束。在弯头的下游,管道内持续的气旋和袋滤捕尘室用以捕获微粒,最后空气被排放到大气中。
图4.实验流量隧道的示意图
实验弯头是一个标准的90°弯头,r/D=1.5(其中r是弯曲半径,D是管道直径,见图1a)。 如图3所示,弯头由两块铝块(Al级6061)螺栓连接在一起加工而成,在弯头内形成均匀光滑的表面。以这种方式构造弯管使其能够容易地从流动通道中移除,分开,并使用坐标测量机测量弯管的内表面。
3.方法
通过重复测量弯头表面,然后在已知且确定的侵蚀条件下,来预测实验弯头中的侵蚀分布。在安装到流道中之前,使用坐标测量机测量弯头拱背两侧的表面。 然后将弯管安置在流道中,用鼓风机启动气流,并以给定速率将砂子送入流量隧道。一旦一定已知数量的砂子穿过隧道,关闭鼓风机,再次移除弯头,并用坐标测量机测量表面。 然后再将弯头重新安装在隧道中,并重复了这一过程。通过减去弯头中每个位置处的表面的连续测量位置,确定从垂直于表面的每个位置侵蚀的材料的量,并绘制侵蚀分布。
使用位于鼓风机上游的经校准的圆锥形差压流量测量装置,来监测通过流量通道的空气流量。然后调节鼓风机的速度以提供通过弯头所需的体积速度。将砂子引入试验段的上游(见图4),以便砂子到达测量弯头时能够相对均匀分布。 通过稍高于大气压的料斗将沙分批进料到系统中,并通过球阀控制砂的输送。 实验中使用单一的输沙速率,即0.030kg / s。通过记录每个料斗负载内已知质量的砂的排空时间来测量砂的速率。
- 实验条件
表1
表2
图5.粒度分布。
实验所用的条件列于表1中,而粒度分布详见表2。假定空气在环境温度为25°C时从外部进入流量通道。大气条件假定为标准大气压力和密度,空气粘度规定为1.8times;105kg/mbull;s。砂子由TGS Industrial Sands Pty。Ltd.提供,并被分类为半锋利的“70级砂”。在沙子上进行了两个独立的筛子的尺寸,这些尺寸的组合结果在表2中以数字表示,并且如图5中的图表所示。中值沙子尺寸为184mu;m。在实验之前进行表面轮廓测量,然后在200公斤沙子已经通过流动通道之后,并且在300公斤沙子已经通过流动通道之后再次进行。尽管已经认识到许多工业系统具有高得多的固体负载量,但是特意选择输沙速率足够低以便在后续计算中可以忽略颗粒 - 颗粒相互作用。通过在实验中使用低固体含量,随后的模型验证练习可以研究颗粒 - 壁相互作用对侵蚀的影响,而不会因颗粒 - 颗粒相互作用建模而进一步复杂化。随后的建模运行在6.5节中展示了在对这项工作进行建模时粒子 - 粒子相互作用的最小影响。
5. 实验结果
表面轮廓在图6中以各种不同的形式报告。在图6a和b中,等轴测图分别显示了200 kg和300 kg砂子通过后的侵蚀深度剖面图,其中侵蚀深度由颜色等值线表示。 图像显示侵蚀接近于表面外缘的对称性,而最大侵蚀点位于外缘。 侵蚀深度从最大值向所有方向减小,沿上游(减小theta;)方向的外倾角的坡度最小。 请注意,图6a和b中的色阶在0.1mm的深度以下再加上0.01mm以下的区域,以便在视觉上识别细节。
图6(a)200 kg和(b)300 kg沙子通过后实验确定的侵蚀深度剖面的色轮廓图; (c)200公斤和(d)300公斤沙子通过之后的侵蚀深度剖面的图示; (e)肘部的等距示意图,定义了x-y-z坐标系统,坐标原点“O”和通过肘部的角度theta;; (f)每个轮廓在弯头表面上的位置。 请注意,(a)和(b)中的比例在0.1毫米以下,再低于0.01毫米。
图6c和d以图形形式显示了相同数据的一个子集。 该曲线图显示了肘部内表面上的给定位置的侵蚀深度作为theta;(通过肘部的距离)的函数。
表面位置如图6e和f所示,并标记为A,B,C,...,V,其中A是extrados剖面,V是intrados剖面。 图6c和d中的图显示了所有剖面位置处的侵蚀深度剖面,但是在位置K以外,所有数据基本为零,因此这些剖面位于彼此的顶部并且未标记。 200公斤沙后300公斤沙之后的数据的比较表明沙通道对侵蚀疤痕的累积效应。 侵蚀深度的分布非常相似(比较图6c和d)。 然而,300公斤沙子通过后侵蚀深度的大小比200公斤沙子大50%,反映了撞击表面的颗粒增加了50%。
为了使测量结果能够被其他研究人员轻松使用,附录给出了一个表格,该表格提供了完整数据集的其他子集的数字数据。 附录中的数据在剖面位置A,C,E,G和J(如图6e和f所示)以及theta;的20个值处给出。 完整的数据集在电子表格中作为本文的补充数据提供,并可在线获取。
6. CFD 分析
该CFD分析的目的是介绍使用标准欧拉 - 拉格朗日CFD方法生成的数值侵蚀速率结果,并将其与第5节中显示的三维侵蚀速率数据集进行比较。通过标准流动的数值模拟 使用用于求解雷诺平均Navier-Stokes方程的商业软件包ANSYS-CFX Version 15.0来执行弯头。 模型设置的细节已由作者先前提出[19,20],所以在此仅作简要介绍。
6.1. 模型几何与网络
CFD模型中使用的流动域的几何结构的范围如图4所示,其中提供了所有相关的内部尺寸。为了更准确地将颗粒呈现给实验弯头,从固体颗粒入口上游的短距离模型化了流动域。通过这种方式,肘部上游的质点速度分布更加真实地被捕获。这种方法也避免了需要确保试验台垂直腿内充分发展的空气颗粒流,这可能需要比现有实验室能容纳的更高的流动通道。
表3
lt;
全文共13669字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11645],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


