英语原文共 7 页
与荷兰引进的电动汽车的快速充电技术比较
Jayakrishnan Harikumaran* , Gyorgy Vereczkj**, Csaba Farkas** , Pavol Bauer* , Senior Member, IEEE * Delft University of Technology, Department of Electrical Sustainable Energy **Budapest University of Technology and Economics, Department of Electric Power Engineering E-mail: J.Harikumaran@studenttudelft.nl.vereczki.gyorgy@sch.bme.hu.farkas.csaba@vet.bme.hu.P.Bauer@tudelft.nl
摘要:在本论文中电动汽车(EV)充电是对快速充电(QCR)有需求的,快速充电和电源切换方面是基于荷兰旅行模式进行的建模和比较。快速充电技术的对比方法是基于充电设施访问次数和获得服务的时间之间的关系。额外的电池数会被引入到已被计算的电池交换网络。利用排队理论我们可以估计出一个快速充电站点需要多少充电点/转换车道数量。基于此获得了两种得到潜在峰值功率的方法。
关键词:电力机动性,快充,电池转换,排队理论
Ⅰ.介绍
电动汽车是被看作运输系统的未来,其调度受到现有基础设施的强烈影响。与以化学燃料作为动力的汽车相比,电动汽车因为昂贵和笨重的电池而受到限制,因此要为充电基础装置提供增加能效的可能性。
许多电动汽车的研究是基于实际出行行为的,也表明了电动汽车是有必要配备快速充电系统和慢速充电设备的。快速充电系统通过能量的快速转换帮助车主解决因长时间出行而产生的焦虑。
技术方面明显的选择快速充电补充技术,这种技术能让电池在短时间内获得更多的充电量(50-100kw DC 输出电源)。高能输出不仅对电网是一种负担也会减少电池的使用寿命。对快速充电站另一种可能的技术是电池转换技术(也被称为电池交换技术),即在整个充电服务过程中整个电池将会被另一个型号相同的电池所替代。为实施这种过程,标准化电池和电池的不同所有权模式是必需的。
然而,尚未对之前提到的QCR技术的电网影响以及公用事业公司和电动汽车所有者的成本方面进行全面调查。例如当一台电动汽车在快速充电补充站中接入电源时,大致会在电网上需求54kw的功率。在交通高峰期,如果基础设施,即充电服务单元没有进行合理的规划,那么电网上的负荷及得到服务的等待时间会高的不合理。
获得的基础设施要求(每个站点的服务单元数量)
荷兰移动数据
快速充电站峰值功率需求
快速充电技术使用数据
基于排队理论的快速充电站缩放过程
荷兰某年的交通行为模型
图1.快速充电站使用模式估计
本论文的主要目的是为了调查和比较快速充电补充技术。服务单元的数量,峰值功率需求和万一电池切换,额外的电池需求也要被计算进去。图1中所描述的方法是用于模拟电动车行为并比较快速充电站的基础设施和峰值电力需求的。
荷兰的流动性调查结果(MON,2009)是由荷兰基础设施和环境部提供的每一年的数据。2009年的数据是作为参考使用的,从2003年到2009年为止荷兰的人口流动的变化不太明显。这些结果是一年的主要数据统计成数据库进行公开并形成一个由高分辨率数据组成的在线数据库。
这些流动性数据被用来建立电动车的行驶模式对快速充电站的需求模型。以下信息来自快速充电技术的模型——每年每辆车对快速充电站的使用的平均数,使用的平均时间,如果选择快速充电模式,那么快速充电的能量共享用于移动和电池切换所需的额外电池。
快速充电站,就像今天的加油站一样拥有容量的限制。排队理论就像一种随机数学方法用来缩减快速充电站数量。使用不同的充电策略可以将快速充电站数量保持在最少量。这些服务单元的数量将通过掌握高峰时段来进行优化。峰值功率的比较是基于服务单元与快速充电技术之间的。
II.流动性调查结果
本节描述了电动汽车的流动性模式对电网影响分析的评估。MON,是在此工作过程中个以2009年数据为基础建立的电动汽车流动性模型。
MON调查为研究人员和决策者提供了荷兰人口运输和流动性的信息。MON调查对荷兰人口的代表性人口集进行了分析。交通通过每年的代表性出行数据进行建模。在调查中出行种类看看可以分为七类——通勤(去公司/回家),工作出差,探访/过夜停留旅行,购物,教育相关出行,休闲旅游和其他。
图2. 按行程开始时间划分的一天平均行程概况
这份数据对制定建设快速充电基础设施的政策十分有用。政策制定者可以将充电设施建立在电动汽车用户最需要的点上,从而提高利用率,并对公用设施的负荷分布有更深入的了解。
数据的分布明确的显示出了在一整天中有许多的出行记录都是分布在早高峰的早上7点至9点以及晚高峰的晚上4点至6点。这些数据与美国的NHTS显示的交通状况有很好的相关性。
每种出行类别的出行距离也能从MON调查结果中估计出来。
根据特定行程持续时间的行程时间分布,如果距离已知,我们可以估计出行程速度。这一数据是用来建立估算出行时间这个模型的。所有的行程都是根据行程长度进行分类的,这些数据提供了对车辆日常使用情况和相应的电源要求以及快速充电需求的深入了解。
MON还显示93%的出行是持续一小时甚至更少。若一辆车每天进行一次往返出行或一次回程出行,那么一台车每天至少有22小时是处在停泊时间的。这表明改变电动汽车充电时间有利于可再生能源的整合和最大化电网容量上限。
图3.每种类别的平均出行距离
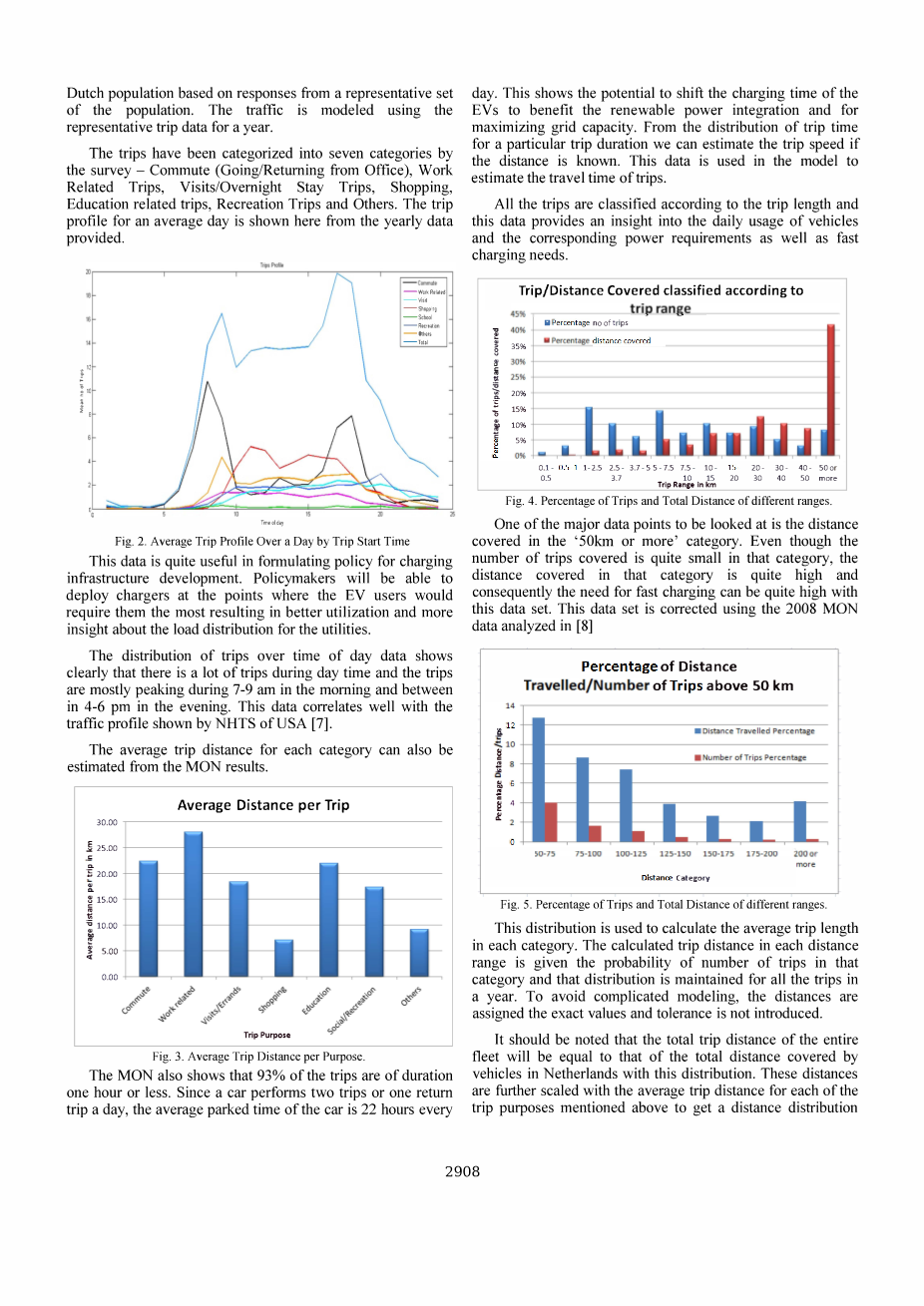
图4. 不同距离的出行百分比和总距离
需要查看的一种主要数据点是lsquo;50公里或以上rsquo;类别中所涵盖的距离。尽管在这种类别在所有类别中占的比例较少,但在这一出行距离中需要快速充电的车辆占比例数据足够高。该数据集使用2008年的MON数据进行修正,该数据集在【8】。
图5. 不同行程的百分比和总距离
该分布用于计算每种类型的平均行程长度。计算出的各距离范围内的出行距离并给出了该类别中出行次数的概率,而且保持了一年内所有的出行分布。为了避免复杂的建模过程,我们都距离进行了精确的赋值,并且没有引入公差。
需要注意的是,整个车队的总行驶距离将等于荷兰车辆行驶的总距离。将这些距离和上述每种出行目的平均出行距离进一步缩放,以获得每种出行目的的距离分布,同时保持总出行距离不变。
由于模型使用了MON调查在线数据库提供的全年出行百分比,所以模型的变化还隐含了旅游模式的季节性变化。
III.电动汽车车队建模
根据第二节里的调查结果来看,能够对荷兰的潜在电动汽车车队行为进行建模。在模型中有一百辆汽车会被降低模拟时间并百分比的方式表达出所需要的结果。在这种情况下,模拟结果可以很容易地扩展到任何数量的汽车上。
行程安排为行程分配了一个距离,根据电动汽车的可用性,选择一辆车,并从车辆中扣除所需的能量,并将其锁定,直到计划回程。根据预计的活动持续时间,返程行程与原行程一起安排。
该距离是从使用该特定目的的机动性调查结果计算的分布中随机分配的,并且根据分配的距离,从查找表中查找速度。这种方法可以确保车队在行程模式中保持随机性。模型没有为每一辆车都分配一种固定模式,因为这样的分配会造成一种理想场景,用户参数全年都会被建模为固定模式。
模型【9】中假定了以下效率值。
表1.
电动汽车各种模块的效率
在建模的过程中,低压充电不能满足来回于家和工作地点(通勤出行)。因此,如果车辆停在某低压充电处充电,车辆将充电3.6千瓦。如果一辆电动汽车的电量不够支撑下次的出行计划或不够完成整个旅途,那么完成行程就需要用到快速充电技术。在这个模型中考虑到了两个选项:快速充电和电池切换,但在特定模拟只能启用一种。如果计划中的目的地有低压充电的机会,只有那么多能量能找到一个更便宜更好的充电目的。
在模型中定义有十九种不同的情况给不同范围的汽车。最低有80公里,最高有170公里,以5的公差递增。下面给出了排队论中用于估计高峰电力需求和服务单位数量的重要结果。(例如,当模型中所有车量行驶里程都是125公里时,Sc125就一种典型场景)。
图6. 不同的QCR技术和车辆范围的访问次数
上图显示了两种快速充电补充技术方法的每年每辆车平均访问次数。与快速充电相比,电池切换的平均访问次数始终较低,因为与快速充电相比,每次切换传输的能量更多。
快速充电的平均充电时间也会在用于估算电力需求时得到并提供。
在快速充电补充技术的电池切换模式中另一个需要考虑的关键结果时完成行程曲线的需要的额外电池数量。下图显示了满足快速充电补充技术所需的电池数量。在切换站,电池以10.8kw的功率充电,获得以下所示结果。
图7.额外电池需求量
在160公里的出行范围的汽车只有33%需要在电池切换站换新电池。安全系数为50%的情况下,我们建议在160公里范围内的车队增加50%的额外电池。
排队论用于估计每一个快速充电补充站的服务单元数量。这是来自电动汽车车队的模型——平均访问数和平均快速充电时间,用于下一张描述的排队理论。
IV.排队理论
就像加油站一样,充电站的容量也有限。某一车辆的充电行为和负载需求是无法克服的,但考虑到大量车辆,可以对某一充电站的使用进行近似计算。对于定标过程,采用随机数学方法,排队理论【10】。排队论已经被用作电话交换机上电话到达过程的交通模型;现在它经常被用来模拟互联网交通流的生成,例如【11】、【12】、【13】或交通管理【14】。也有别的论文已经使用排队理论对快速充电站进行建模(【15】、【16】、【17】、【18】、【19】、【20】、【21】)。本文希望通过对电动汽车充电站参数的研究,扩大这一范围。
选用M/M/c/ N排队理论对快速充电站进行建模。M/M/c/ N是有Kendall引入的一种速记符号,它是排队模型的特征【22】。每一个字母的含义如下【10】,【23】:
- 第一个M:指数分布到达时间
- 第二个M:指数分布服务时间
- c:服务单元数量
- N::系统的容量,可以停留在某个充电站的最大车辆数(包括充电车辆)
服务规则也可以确定。它定义了服务需求的方式、服务需求的顺序以及资源在需求中的分配方式。在计算过程中,采用了最常用的先进先出原则(先到先得)。
排队论的主要特征可以用图8概括。
图8.排队理论的主要数据
到达过程通常用到达需求之间间隔的概率分布来描述。到达间隔的倒数是到达率(【1/min】),通常用于计算和显示到达频率。然而,可以看作是时间函数:这意味着的值在每一瞬间都会改变,在一定的时间内,它是不变的。这些能在图9中显示的日常交通模式里看到。
充电站的容量有限(即充电点/转换车道数量有限,甚至停车位数量有限),因此有些客户很可能不得不等待。论文的目的是对一个充电站进行规模化,该充电站具有最佳数量的充电点/交换车道,能够满足输入的充电请求。图8表现出了如果充电点/交换车道不足,有些客户不得不等待:他们会排队。另外的人能为自己的车充电。很明显,汽车是分批充电的,这意味着许多C车同时充电,其中C表示充电点/转换车道的数量(更正式的服务单位)。正如到达率一样,汽车的服务率也有一个服务率。服务时间的倒数(【1/min】)是服务率,通常用于计算。显示服务单位在一定时间内可以满足的需求数量。
在汽车充满电之后就会离开充电站,这样下一个等待客户就能充电了。
A.排队理论指标
排队系统的效率和性能能用以下指标衡量【24】,【25】:
1)利用效率【】:利用效率,也称为交通强度,描述服务单位是否能够处理到达需求。利用效率可定义如下:
) (1)
如果,传入的需求到达的速度比服务过程能够为它们服务的速度要快。这样做的目的是确定利用效率,以计算服务于一定到达率的最小服务单元数。如果服务单位(c)的数量包含在以下公式中,则利用效率将表示为“a”,并用于以下计算中
(2)
2)平均队列长度【N(s)】: 平均队列长度定义为队列中等待的平均需求数:
(3)
,其中是系统中不需要的概率。被称为平稳分布。其计算见【10】】、【11】、【23】,
3)系统中汽车的平均数量【N(r)】:系统度量中的平均车辆数定义了系统中充电和等待需求的总和。
(4)
4)系统中平均花费时间【T
资料编号:[5366]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。