锥面与球面螺旋槽轴承
(第二部分:负载能力和稳定性)
J.Bootsma
荷兰,埃因霍温,飞利浦实验室
在第一部分开发的理论应用于解决实践中遇到的问题。轴向和径向的承载能力和刚度取决于轴承尺寸,特别是槽的尺寸。锥面与球面螺旋槽轴承稳定性与螺旋槽轴承轴颈稳定性有关,甚至在不承受径向载荷的情况下也能稳定下来。让这些在卸载状态下的轴承稳定下来的一个必要条件是在轴承间隙中填充润滑剂。在不完全填充的情况下,轴承间隙的气-液交界面和压力分布在润滑膜中的交互作用,会使轴承具有负刚度。
术语
圆锥轴承B=轴向宽度 =轴向分力
=径向跳动 载荷向量
=轴向跳动 R=轴承的外径
=槽的深度量纲 =无量纲向量最小量纲
锥形轴承
M=质量转子 =平均值之间的径向间隙
P=因次平滑的压力 =槽的角度
=垄宽比为宽度槽
=维度的切向分力 =角对着一个填充球面
少载荷向量 轴承润滑油的同心位置
=自由边界的幅度 =动力粘度
=圆周坐标 =自由边界的相位角
=或,取决于是否平转或仅开槽部件旋转
=旋转频率,其中,如果纯部件旋转
或取决于仅平转或仅开槽部件旋转
星号*表示数量
简介
第一部分作者介绍的处理方法依赖于在球面和锥面螺旋型槽的轴承间隙压力分配及牛顿可压缩液体润滑剂填充的理论。在这个处理方法中,对轴承间隙中是否填充完整液体做了一个区分。在完全填充的轴承间隙处没有气液交界面的产生,因此我们可以说这是一个固定边界。在未完整填充的轴承间隙处遇到气液交界面,或者说自由边界。自由边界和压力分配的位置,与润滑膜分布有关。
在第一部分我用数学模型对自由和固定边界进行分析当径偏心距时找到了轴偏心距的各个值的精确值。在时,在数量上的线性接近,则获得装置中扰动方法的的函数。
在第一部分对这个理论得到的结果的精度进行了研究。有人说,在结果中得到的扰动方法只要实际中没有发生气蚀都可以采用扰动法。
本文件将处理所得的成果:扰动法。而且大部分的注意力都将投入到这一部分。与注入不可压缩的润滑剂的滑动轴承相比后发现,螺旋槽轴承甚至可以在径向卸载状态下保持稳定。
虽然在第一部分我公司开发的理论是适用于任意槽型的螺旋形凹槽轴承的,但在这一部分只关注矩形槽。
在对球面凹槽分析后,发现槽形仍指向于南极。这不可能在实际中出现。但是槽形产生的效果不能一直对轴承的南极产生影响(例如:当)。对外球面轴承运转影响小。
球面锥形螺旋槽轴承的间隙完整填充润滑剂
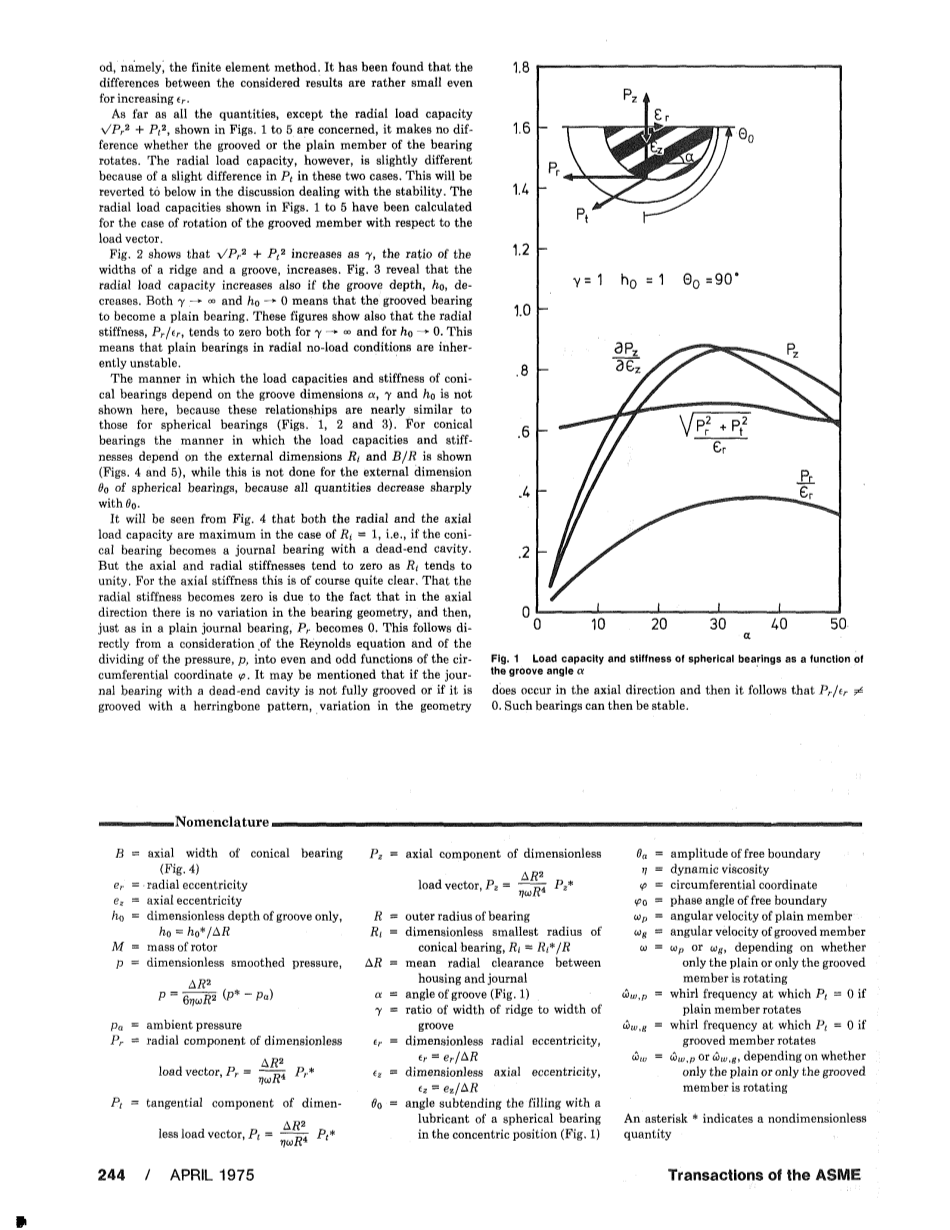
轴向和径向承载能力和刚度。轴向承载能力,径向承载能力,轴向刚度,径向刚度,他们取决于球形和锥形轴承带固定边界的螺旋槽的几何量。几何量与当径向刚度最大时的几何图形是不同的。在一个的圆面轴承中,如果槽的参量,,,那么是最大的,在一个锥面轴中当,我们发现当,,,时有一个最大值。
在第一部分的表达式,和取决于参数和,参数和独立于,而也独立于,这些参数和一起被计算出来了,一些结果如图1-5所示,结果中的与被应用到所有的和中,其产生的误差为和。结果中的数据和被应用到和所有中,其产生的误差为:在第一部分中,这些误差的大小通过比较分析近似数值方法,既有限元法。已经发现,得出的结果间差距非常小,甚至对于增大的也一样。
至于所有的参量,如图1-5而言,除了径向载荷能力外,无论是槽还是轴承的滑动构件旋转都不受昼夜温差的影响。它的径向负荷能力是稍有不同的。因为在开槽区上有两种情况,则会回到正在处理的稳定性的讨论上。改图中所示的径向负荷能力在图1-5中已经被计算为槽件的转动相对于上述情况下的载荷向量。
图1 球形轴承的承载能力和刚度关于槽的角度alpha;的函数图象
图2显示增加为gamma;,脊和槽宽度之比也增加了。图3表明,该径向负荷能力也增加,但前提是槽的深度减少。和都表明开槽的轴承变成了一个滑动轴承,这些图还表明,无论是还是,径向刚度往往都为零,这意味着在径向卸载条件下,滑动轴承总是不稳定的。
负载能力和刚度是以何种方式依赖于槽尺寸参量,和。在这里不显示出,因为这些关系类似于那些球面轴承的(如图1,2和3)及锥形轴承的形式,其中负载能力和刚度取决于外部尺寸和将会在图4,5中显示,然而这对于球面轴承的外部参数,还是不够的,因为所有参量在作用下都在急速下降。
|
图2 球形轴承的承载能力和刚度关于脊槽宽之比的函数图象 |
图3 球形轴承的承载能力和刚度关于无量纲的槽深度的函数图象 |
在图4中我们可以看出,无论是径向还是轴向负载能力都满足。锥形轴承由轴颈和封闭腔构成,但轴向与径向的刚度倾向于零,日趋于统一。对于轴向刚度,这显然非常明确。该径向方程和刚度变为零正是基于此,即在轴向方向的轴承几何参数上没有变化,然后,就像滑动轴承一样Pr变为零,直接从考虑雷诺方程和分压力p的角度出发并引入具有奇偶功能函数坐标,它还提到,如果具有封闭腔的轴承未完全开槽或者是一个螺旋槽,变化肯定在开槽的几何轴向上,然后使它遵循。这种轴承可以保持稳定。
|
图4 锥形轴承承载能力和刚度关于的函数图象 |
图5 锥形轴承承载能力和刚度关于的函数图象 |
图4示出了负载能力和圆锥轴承刚度的函数,图4还示出了轴向刚度的增加和的减少的函数变化,在情况下,类似全槽球面轴承的几何沟槽轴向刚度。这种相似性具有更广泛的适用性。有可能对于各种螺旋轴承都适用,所以对圆锥形和球形以及推力轴承也适用。在该区域中的槽分布均匀并具有恒定膜厚,超出这个地区则没有凹槽,无量纲轴向刚度偏导(1)。其中是在第一部分中定义的函数,它只取决于凹槽的形状。
(1)
图5显示当增大,圆锥轴承的径向载荷能力大大增加,轴向负荷增加较少,而径向刚度的增加依然很少,它的大小取决等式(1),该轴向刚度是独立于的。(特别指出,在纵坐标变化范围很小的图中,图5和所有其他插图都是系统发散的)
在表1中,球形、圆锥形的特征量与已收集的两个轴颈轴承凹槽参数总是不同的。该期刊有完整的螺旋槽轴承样品,经比较后最终确定选择是为了保持三种类型的轴承外部参数相同。
轴颈轴承也可以视为轴颈与轴承是一个封闭腔和螺旋槽。则三种类型的轴承的运转规律相似度就会很大,并且球形和锥形轴承使矩形槽和轴颈轴承的螺旋槽更加统一。
具有的槽的轴向载荷能力最大[1].在其他的形状的槽中,径向刚度总是最大。在一个轴承的情况下,当[2]径向刚度为最大。而参数的轴承的径向刚度则是接近最大值。
为完整起见,因为不同于上述两种情况,该表还包括稳定的标准和轴承径向的摩擦损失。径向负载能力的大小取决于是否开槽建或轴承滑动构件相对于所述负载的矢量旋转。同样对于稳定性,轴承槽在旋转和静止条件下是不同的,这一点将在后面给予更多的关注。
稳定性。螺旋槽轴承相对于滑动轴承的一个重要特征是,他们可以在径向载荷减小状态保持稳定。这些径向并非唯一指将被考虑的稳定性轴承,而会进一步调查带有刚性转子和刚性安全衬套的轴承。
轴承稳定性是一个非常复杂的问题,不受干扰的回复力是一个非线性函数,我们需要暂时搁置之前的轴承,通常情况下,回复力被线性化,使它可以在弹簧中表达成阻尼条数[3,4],动态性能可以再由一组线性微分方程来描述,这种线性化能先降低有关稳定性问题的难度系数。带有刚性转子和刚性安装套的轴承在径向载荷减小情况下研究轴向和径向的稳定性是现行理论,根据可知取决于,径向载荷减小状态的径向稳定性通常是最关键的,因此径向的稳定性将得到进一步研究。
从线性理论对径向稳定性的物理解释将从现在开始给出[3]。对在套管中心线上以为半径的圆轨道中以特定扰动频率回旋的轴,它受到一个离心力在经受干扰的情况下,径向矫正的回复力将只有一个值把这个回旋频率称之为特征回旋频率。因此,当时,和决定回复力。从平衡恢复力和离心力讲,如果并把作为这方面的标志,如果,(2)那么扰动频率会降低。从线性理论讲它遵循(2),这仅仅以径向卸载轴承的径向稳定性为标准(3),在无量纲形式中,径向载荷减小的球面轴承的径向稳定性具有固定的边界,并与径向刚度最大的槽形一起被考虑。为了研究特定回复频率的稳定性,在时必须被确定。因此图6在关于套管中心线回旋频率为的情况下,和作为的函数被展示出来。由图可知是独立于而且与具有线性函数关系。它可以使用第一部分的理论说明,这适用于所有的具有固定边界的球面和锥面轴承。
对于确定特征回旋频率当回旋频率中时,必须区分纯原件和槽原件的旋转。这两种情况将在图6中展示出来。
对于普通的原件的旋转,横轴出现在中间,而对于槽原件则出现在底部。这两种情况之间的关系是基于以下事实,对于平滑压力偏微分方程和边界条件(参见第一部分),在平滑压力满足表达式两个特征回旋频率 和的关系是[5],如果,它对稳定性会有影响,并且也对径向负荷能力有影响;在普通构件或槽构件中都存在影响。
|
图6 带有固定边界的球形轴承的回复力的径向和次要组成关于回旋频率的函数图象 |
图7 带有自由边界的球形轴承的回复力的径向和次要组成关于回旋频率的函数图象 |
表1是给出对轴承径向稳定性判断依据,对于其他槽形的径向卸载轴承的稳定性判断也在表1中给出了。
球面锥形螺旋槽轴承间隙处于不完整填充
在上面我们只关注了完整填充的轴承的运转,现在,让我们看一看未完整填充将有什么影响。
在轴承间隙未完整填充润滑剂时,气液界面和自由边界将会出现。若径向偏心距为零,那么自由边界的位置是独立的周向坐标,前提是小杂物在槽中对系统的蒸发散失不包括在内。在径向偏心距确定的条件下,自由边界位置也由周坐标决定。在润滑膜中压力的分布与自由边界位置的确定是有相互影响的。第一部分的理论确定所述的自由边界的位置和润滑膜上的压力分布。这个理论假设该气液界面的位置不依赖于表面张力和惯性力。在锥形槽轴承的稳定性被证明是真实的[5],但是,气液界面可以存在的依据是在过大的角速度中的表面张力。例如,表面张力不再能避免气液界面的损漏[6]。
正如已提到的螺旋槽轴承相对滑动轴承甚至可以在径向卸载时保持稳定这一比较重要的特征。现在让我们看看在轴承间隙在不完整填充的锥形和球形螺旋槽中是否也如此。在带有固定边界的情况下,对于稳定性的研究将受限制于具有刚性转子和刚性安套管的径向卸载轴承的径向卸载稳定性。另外,另一种自由边界稳定性判断依据由方程(3)给出,但在是液体在轴承间隙量较少时()将受到详细考虑。
为了更稳定的调查,有必要确定特定回旋频率和在时的数值。因此扰动发生在一个轴的情况下,我们一直研究在左右套管中心线的圆形轨道以频率旋转的情况。这种扰动影响自由边界的位置,也对计算有影响。在图7展示回复力的两种情况,纯原件和槽件的旋转转动与有边界的轴承不相似,不再独立于,且未显示与的线性关系。这意味着测定特征回旋频率和的值比在一个固定的边界情况下变得更复杂。该图显示对特征回旋频率有负影响。这意味着,径向卸载轴承是内在不稳定性。
图8 自由边界的角度和相位角关于的函数图象
该图中还显示,在一个固定边界情况下,如果径向稳定条件遵守[3]那么为正有自由边界的轴承恢复力有卓越表现在图7中可显示出来。而且负刚度将在下面做出解释。在轴承间隙的压力分布是由于楔形效应和槽的作用。该楔形效应为几乎为零,压力分压主要由于凹槽效果。当时唯一重要的是自由边界的形状。是进一步发展而来的,自由边界上形状更小的效果,则其上的复原力就变得越大。这种自由边界的形状
(6)
其中和可以按第一部分描述的理论计算出来。图8中,在球形轴承的情况下,和已被制成的函数图表。我们可以看到,特征回旋频率和相位角都趋近于零。这意味着最大时接近间隙最宽处。最小接近最窄处,在带有回旋频率的自由边界形状的轴承压力分布及轴承呈辐射的其刚度是负的也是可能的。
参量也已计算出球面锥形轴承具有不同的均匀凹槽图案,在发生自由边界时它已发现径向刚度总为负。另外,在球面轴承去不同值时及锥面轴承的和取不同值时,它总是发现在发生自由边界时这些轴承在径向卸载状态是不稳的。它应当指出,在改情况下没有考虑不均匀的槽形图案,例如人字形槽,在径向卸载状态下,发生自由边界也有可能保持平衡。
结语
主要结论是在球面锥形螺旋槽轴承未完全填充润滑剂而在润滑膜上出现(自由边界)气液交界面时,径向卸载状态的锥形和球形螺旋槽轴承具有固有不稳定性。另一方面,那些在轴承间隙完全填充且持续完整填充润滑剂的轴承能很好地保持稳定性。在有固定边界的情况下,已经显示出径向和轴向承载能力如何,沿径向和轴向的刚度取决于最重要的轴承和沟槽的尺寸。
剩余内容已隐藏,支付完成后下载完整资料

英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[150203],资料为PDF文档或Word文档,PDF文档可免费转换为Word


