随机环境下班轮运输动力学确定及班轮加油口选择外文翻译资料

英语原文共 26 页，剩余内容已隐藏，支付完成后下载完整资料

随机环境下班轮运输动力学确定及班轮加油口选择

摘要 ：在这项工作中，我们研究了一个班轮运输业务问题，该问题考虑了如何动态确定船舶速度和加油决策，对于一条航线中的单船。我们的模型是一个多阶段动态模型，其中燃料价格的随机性由场景树结构表示。此外，我们明确将燃料消耗率的不确定性纳入我们的模型。由于该模型是一个大规模的混合整数规划模型，我们采用修正的滚动时域方法来解决这个问题。数值结果表明，与相关工作的平稳模型相比，我们的框架提供了更低的总体成本和更可靠的时间表。

关键词：班轮运输；船速；油价；燃料消耗率；情景树生成；滚动时域

第1章 绪论

近年来，燃油价格上涨的趋势已经威胁到班轮公司的财务底线。为了生存，公司需要找到降低运营成本的方法。例如，2008年油价到达每桶145美元时，全球最大的班轮运输公司马士基率先推出了减速运航的战略。现在有200多家航运公司降低了航速，特别是在亚洲到欧洲和北美等长途航线上。经验估计表明，当船只速度降低20％时，它可以将油耗降低50％。尽管船舶班轮必须在特定航线上增加一两艘船来保持每周服务，这会导致资金成本以及行政管理和人工成本的立刻增加，但燃料成本的节省可能会超过那些成本增加。此外，减速运航排放的温室气体排放对环境的影响也很大。马士基宣布，他们在2008年成功地将平均每艘船的二氧化碳排放量减少了14％。

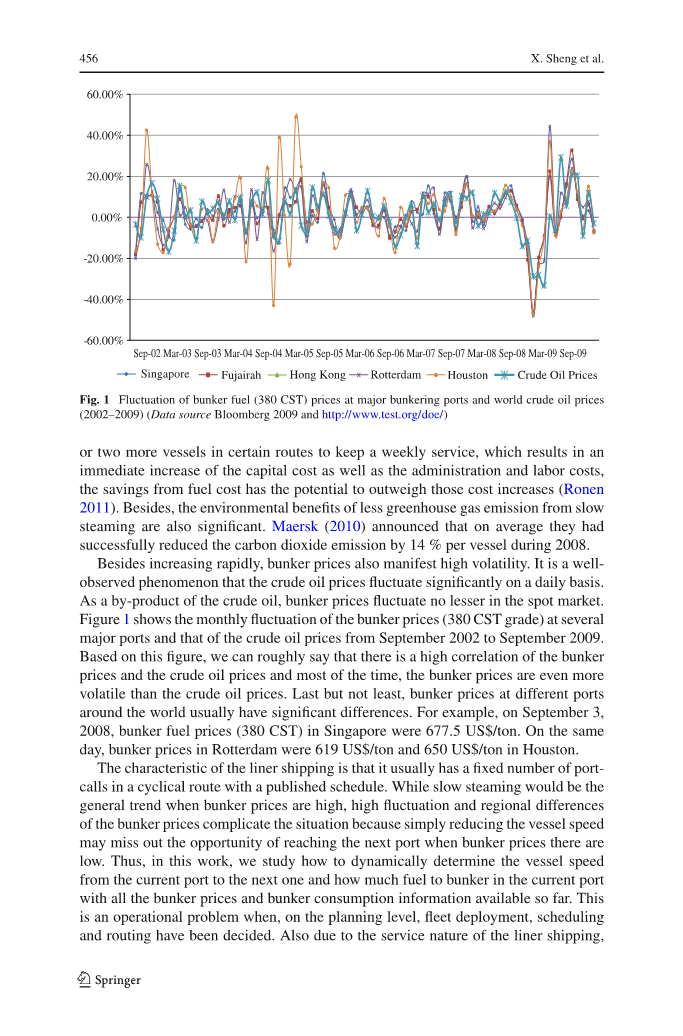
除了快速增长之外，燃料价格也表现出很大的波动性。原油价格每日大幅波动是一个令人欣慰的现象。作为原油的副产品，现货市场燃料价格波动不小。图1显示了2002年9月至2009年9月几个主要港口的原油价格（380CST级别）和原油价格的月度波动。基于这个数字，我们可以粗略地说，燃料价格和原油价格以及大部分时间，燃料价格比原油价格更加波动。最后，但并非最不重要的是，世界各地不同港口的燃油价格通常存在显着差异。例如，2008年9月3日，新加坡的燃料油价格（380CST）为677.5美元/吨。同一天，在鹿特丹的燃料价格和在休斯顿为619美元/吨和650美元/吨。

班轮运输的特点是它通常具有固定数量的沿途港口，并且具有公布的时间表。当燃料价格高时，减速运航将是总体趋势，燃料价格的高波动和区域差异使情况复杂化，因为简单地降低船只速度可能会错过当燃料价格较低时到达下一个港口的机会。因此，在这项工作中，我们将研究如何动态确定当前港口到下一港口的船舶速度，以及当前港口燃料到目前为止的所有燃料价格和燃料消耗信息。在规划层面，如果机组部署，调度和线路已经确定，这是一个运营问题。同样由于班轮运输的服务性质，如果不考虑转运，相同航线的船舶与不同服务航线之间的相互作用非常低。因此，我们的研究只需要在一条航线上考虑仅一艘的船舶，只是因为船舶和航线的运营独立性。

以前的大部分相关工作都没有充分解决这个问题的不确定性。罗恩研究了缓慢航行带来的燃油节省和航程延长带来的收入损失之间的贸易。它将日常燃料消耗估算为船速的三分之一，并推导出在不同运营情景下的船舶的最优速度，即收入产生支线，定位支线和混合支线。Perakis和Papadakis研究了成本最小化问题，即固定合同价格下的固定数量的货物需要在一个装货港和一个卸货港之间的特定时间段内由船队按照固定合同价格交付。通过选择最佳的满载和压载容器速度，总的车队运营成本被最小化。它将通用燃料（包括推进燃料和船舶运行期间使用的所有燃料）的速率建模为船舶功率的二次函数，作为回馈，其以船速的幂函数表示。在随后的研究中，Perakis和Papadakis用多个装卸港口扩大了这个问题。Notteboom和Vernimmen研究了面对高燃油价格的班轮运输如何调整班轮服务时间表。在这项研究中，作者提供了关于不同大小集装箱船的每日燃油消耗与船速之间关系的实际数据。从显示的数据中，我们可以看出，不同尺寸的船舶的燃料消耗率与速度实际上是不同的，尽管作者没有研究这个问题的细节。Ronen调查了在减速运航和在集装箱路线上添加额外船只之间的权衡。其目标是通过最佳船舶速度和部署船舶的数量来最小化该路线的年度运营成本。

Yao研究了一个与我们的性质类似的问题，但在他们的研究中，重点放在了计划水平问题上，因此没有解决不确定性问题。关于燃料消耗率与船速之间的关系，他们分析了不同尺寸船舶的分析结果。另外，不是假设一个单一的三次关系，而是在回归模型中增加了一个常数系数，通过数值实验证明它们不是微不足道的。在所有上述研究中，燃料价格要么假定为恒定或者没有明确考虑。

图1 主要加油港口和世界原油价格（2002-2009）的燃油（380CST）价格波动

Oh和Karimi提出了一个混合整数线性规划模型，该模型在不确定的燃料价格下优化了多包油轮的运行。然而，在解决模型之前，只有少量的独立价格情景产生。因此，它本质上是一个固定的模型。Besbes和Savin对两种类型的船舶，即“班轮”和“帆船”构建了一个动态的利润最大化问题，并推导出了最佳的加油政策。在班轮情景中，问题归结为加油成本最小化问题，受到随机燃油价格和船舶燃料容量的限制。然而，船舶航行速度在问题描述中给出，未考虑燃料消耗的不确定性。他们将燃料价格建模为三部分的总和：现货原油价格与全球价格调整因素，燃料价格的当地供应修正因子以及由于其他因素导致的地域调整。现货原油价格采用AR均值回复过程进行预测，并将当地供应修正因子描述为两州Markovian过程。

据作者所知，没有公布的结果考虑到燃料消耗的不确定性。然而，风力和方向，海况，发动机效率等因素都可能在很大程度上影响燃油消耗。只有以任何速度考虑消费率的随机性，我们才能更精确地捕捉真实世界的情景，并为班轮运输从业人员提供更可靠的运营水平建议。因此，我们的工作是在考虑燃料价格和燃油消耗率不确定性的同时，首次尝试解决速度决定和加油决策。

我们将把我们的问题表述为一个多阶段动态模型，其中燃料价格不确定性由情景树结构表示。由于该模型是一个非常大规模的混合整数规划模型，我们采用修正的滚动时域方法来解决这个问题。

本文的其余部分组织如下：在下一节中，我们将对我们的问题进行一般性描述。将讨论不确定燃料价格和日消费率的建模。在第3节和第4节中，我们提出了我们的动态模型和改进的滚动时域求解方法。两个案例研究将在第5节。最后，结论和未来的研究将在第6节中介绍。

---------------------------------------------------------------------------------------------------------------------

第2章 问题描述

在本文中，我们考虑在一个周期性航线（从一个港口开始，经过所有其他港口至少一次并返回到原始港口）的单线班轮的运营层级决策制定，具有固定数量的港口呼叫和时间视窗。时间窗口显示每个港口的船舶到达和离开时间。在我们的工作中考虑的两个不确定因素是燃油价格和燃油消耗率。本节后面将详细讨论如何捕捉这两部分的随机性。

两个关键的决定是在哪里和多少供应燃油。在实际操作中，在下一个港口到达之前，船东会询问燃油供应商的报价，据此做出燃油决定。一旦确定，报价将很少改变，直到船到达港口。因此，我们可以方便地假设，只有当船舶到达一个港口时才会发生加油。由于当地的供需因素，加油决定取决于每个港口的燃油价格，这些港口在这些港口通常是不同的。每个港口燃油价格的演变可以模拟为一个离散时间的Markovian过程，描述这些状态之间所有可能的状态和转换矩阵。在不失一般性的情况下，我们假设港口呼叫是每周进行的，因此我们只需每周描述一次港口价格的变化。虽然这是我们工作的一个缺点，但滚动时域方法可以帮助缓解这个问题。这是因为我们总是可以根据适时的真实世界情况更新船用燃料价格情景树。

除了加油之外，另一个重要的决定是每条支线之间的船速，在每条支线通常被假定为恒定。如何在预定的到达时间内到达每个港口，并通过减速运航来节省燃料消耗，这是大多数从业者面临的问题。传统上，船舶设计为高速航行。根据船舶制造商的建议，利用低于发动机负荷40％的转速被认为会损坏发动机。然而，马士基在2010年其自己的110艘船上进行的实验表明，如果有必要，船可以放慢速度。

在我们的问题中，目标是最大限度地减少一个服务循环中的总运营成本。这里考虑的成本是燃料成本和库存持有成本。燃油成本主要由两部分组成，即每次燃油添加时发生的固定燃油补给成本以及当时取决于燃油补给量和燃油价格的可变成本。库存持有成本可以解释为购买燃料时承担的资本的组合，否则这些资本可能通过一些投资活动产生利润，而由于运载创收货物的能力较小，收入损失。作为简化，我们假设每吨的库存运载成本（pmt）是恒定的。因为我们的研究视界是一个有限的服务循环，所以不可避免的是，在航行结束时在船舶油箱中将留下燃料。对于剩余的燃油量，我们根据当时的燃油价格从总成本中扣除。

2.1燃料价格模型

为了模拟燃油价格的演变，我们使用航程每一段的百分比变化，但困难在于百分比变化可以在合理范围内采取任何连续值。将具有连续分布的随机变量合并到优化模型中会使得模型非常困难，甚至不可能。

表1 每日燃料消耗率分析

因此，我们对燃料价格百分比变化进行离散化，并假设它们遵循Markovian过程，这意味着当前燃料价格仅取决于前期价格百分比变化。首先，我们确定一个区间，在这个区间内燃料价格百分比在两个后续时间段之间可以发生变化，然后我们将这个时间间隔分成几个较小的子区间。描述这些子区间之间的转换矩阵被构造。最后，选择一个离散点值来表示每个子区间。我们可以选择子区间的均值或通过随机抽样生成它。

例如，如果我们将Pit和theta;it表示为港口i和时间段t的燃料价格和燃料价格百分比变化，Pi0表示作为港口i和时间0的基准燃料价格，则在每个港口和时间的燃料价格期间t基于基准燃料价格以及前几个时期的所有百分比变化。例如，Pi1=Pi0times;theta;i1，Pik=Pik-1times;theta;ik。如上所述，在我们的工作中，我们通过每周燃油价格变化演变来估算逐个港口燃料价格变化的演变。

2.2 燃料消耗率模型

Yao假设每日燃料消耗率可以表示为F=k1·V3 k2，其中k1和k2

全文共21402字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[15517]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 船舶舵机PLC控制设计外文翻译资料
• 减少排放的海洋技术外文翻译资料
• 巴拿马型集装箱船和大型油轮的新经济性引擎外文翻译资料
• 基于均载的非对称高接触比直齿圆柱齿轮承载能力研究.外文翻译资料
• 水轮机组件中的空蚀和抗空蚀涂层的研究现状和发展需求外文翻译资料
• 基于GIS的信息共享基础设施使用数据挖掘和视觉技术的集装箱港口物流外文翻译资料
• 采用遥测方法测量内燃机中的活塞温度外文翻译资料
• 排水量17000吨的油船动力装置设计外文翻译资料
• 4300DWT油船动力装置设计外文翻译资料
• 耙吸式挖泥船的建模沉淀过程外文翻译资料