
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
大功率柴油机曲轴动态特性模型
摘要:发动机部件在恶劣条件下的动态行为很难掌握。 在本文中,研究了Deutz F8L413直喷式空冷柴油发动机在恶劣工况下曲轴的动态特性。发动机的最大运行特性是在配备液压制动器的台架测试中进行实验测量的。通过数值模拟确定了曲轴受最大应力的区域。另外,使用两个疲劳标准来分析曲轴的疲劳行为。 通过比较数值结果和使用自然模式的振动测试获得实验数据来证明模型的有效性。
关键词:曲轴,动态特性,疲劳,振动,重要功能
1,引言
汽车曲轴在使用过程中会承受大量的循环载荷,导致许多疲劳和振动问题。对于V型汽缸发动机的特殊情况,这些动态现象更为明显,可以在最大发动机负荷情况下清楚地识别,即对应于最大功率和扭矩的状态。
由于几何结构的复杂性和所涉及的许多相互作用,人们对基于简化模型的动态曲轴领域进行了许多研究。对曲轴进行大的静态和动态分析以提高其耐用性(Henry et al,1992)和性能(Dimbale et al,2011)。Nikolic等人开发了一种算法,以通过将曲轴视为梁来获得IC发动机曲轴主轴承的理论磨损图。 (Niinoa et al,2002)通过测量实验测量V型缸发动机的曲轴动态特性,测量曲柄销在高低转速时的应力幅值。Ccedil;evik和Guuml;rbuuml;z2012年的研究证明了曲柄销滚动对用于柴油发动机的球墨铸铁曲轴疲劳行为的影响。基于梯度测试方法,他们进行共振弯曲疲劳测试以获得应力与循环次数曲线进行比较,并评估曲轴销滚动和未滚动条件下球墨铸铁曲轴的疲劳寿命极限。 V型汽缸发动机的优点之一是,与同等的直列气缸相比,它们大大减少了整个发动机的长度,高度和重量。研究发现,如果将同样性能的6缸直列式发动机转换为V型发动机,则其初级和次级力矩的幅度降低至50%(Ide et al,1990)。Niinoa等于2002开发了一种分析内燃机曲轴动态特性的系统模型。该模型结合了曲轴的动态结构,主轴承的流体动力学润滑和曲轴箱的刚性。最近,基于缸内压力估算的发动机动力学模型的实验研究正在进行。在(Taraza,2002; Schagerberg和McKelcey,2003; Larsson和Schagerberg,2004)的方法中使用了更复杂的多自由度发动机动态模型,以通过利用曲轴集成扭矩传感器来估计缸内压力。然而,对于曲轴的三维模型,特别是在最大负载条件(最大功率和扭矩的状态)下V型气缸的发动机上,只进行了很少的研究。这些最大负载的实际条件允许对动态应力水平进行真实的预测,这对于动态响应的持久性,轻量化和优化非常重要(Kim和Woo,2013)。AR等人所提出的抗疲劳性也很重要。
本文利用实验测量推导出的最大载荷条件,在台架试验中研究三维模型,以确定V型汽缸的柴油机曲轴的动态行为,并以四个(4)曲柄销为例,研究F8L41型Deutz柴油发动机。这款风冷的发动机载荷很大。本模型的新颖之处在于,参数是从用于识别曲轴的动态行为的发动机实际工况获得的。本文步骤如下。首先,通过在台架测试中收集的实验数据确定最佳标准(最大功率和扭矩以及最小特定油耗)。接下来是活塞和连杆的运动学和动力学表征,其目的是确定通过连曲柄连杆机构在最大限度确定的标准下对曲轴施加的作用力。然后提出了流体动力轴承 - 曲轴接触模型以及曲轴的三维有限元建模。给出了仿真结果和后处理。进行疲劳计算,确定振动模式。振动测试是在实验室中进行以确定自由曲轴的特征模式(无飞轮),并与数值模拟中的特征模式进行比较。
-
台架实验研究
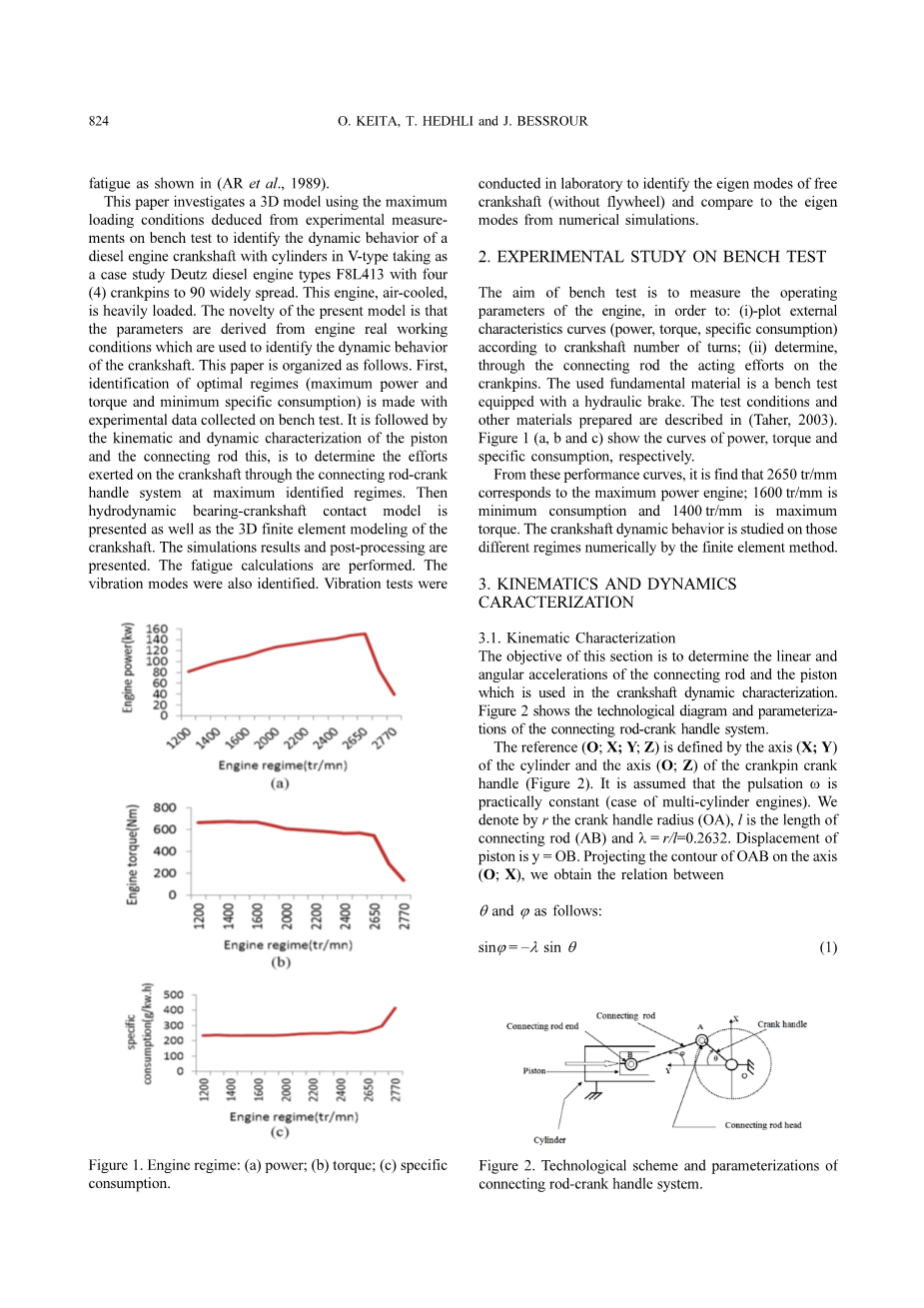
台架测试的目的是测量发动机的运行参数,以便:(i)根据曲轴转数绘制外部特性曲线(功率,扭矩,油耗); (ii)通过连杆确定曲柄销上的作用力。使用的基本条件是配备液压制动器的台架测试。 (Taher,2003)描述了测试条件和其他工具。图1(a,b和c)分别显示功率,扭矩和比耗的曲线。
从这些性能曲线可以看出,2650 tr / mm对应于最大功率;最小油耗为1600 tr / mm,最大扭矩为1400 tr / mm。通过有限元方法对这些不同状态下的曲轴动力特性进行了数值研究。
3,运动学和动力学分析
3.1,运动学表征
本节的目的是确定连杆和活塞在曲轴动态表征中使用的线性和角加速度。图2显示了曲柄连杆机构的工艺图和参数化。
参考(O; X; Y;Z)由气缸的轴线(X; Y)和曲柄连杆机构(图2)的轴线(O; Z)确定。假定脉动omega;实际上是恒定的(多缸发动机的情况)。我们用r表示曲柄手柄半径(OA),l是连杆长度(AB),lambda;= r / l = 0.2632。活塞的位移是y = OB,将OAB投影到轴(O; X)上,我们获得了OAB之间的关系和如下:
————————————————————————(1)
考虑到cosphi;ge;0(见图2),我们得到:——————(2)
3.1.1,连杆的运动学
通过推导方程(1)并考虑方程(2),我们获得连杆的角加速度为:————————————————(3)
因此连杆的线性加速度由以下关系表示: ———————(4)
关系(3)和(4)的详细计算在附录A中解释。
3.1.2,活塞的运动学
将OAB投影到(o,y)上并考虑方程(1),我们得到活塞的加速度如下:
—(5)
3.2,动态特性
用于曲轴和活塞的机械运动的减速元件在曲轴和连杆的轴上减小一个力, 其动量是运动部件加速度的函数。为了计算这个动量,有必要确定施加到连杆头部和脚部的机械动作。F8L413型柴油发动机是V型8缸发动机。四个曲轴销中的每一个都安装在连杆的两个头上(图3)。V型多缸发动机由两个直列式发动机构成,偏置角度delta;=(Y1,Y2),称为V型张角(图3)(Swoboda等,1998)。在我们的实验中V型张角delta;=4pi;/ 8 =pi;/ 2。假设FA1和FA2分别为A点处连杆(b1)和(b2)上曲柄销施加的力,FB1和FB2中活塞施加在连杆(b1)和(b2)上的力分别为分别为B1和B2。
3.2.1,连杆(b1)的情况
连杆(b1)在其重心G1(也是其惯性中心)处的加速度的转矩量的减少元件是delta;G1(b1)和mb1Gamma;(G1)mb1,也是连杆(b1)的质心。XA1,YA1,XB1和YB1分别是(O; X1)和(O; Y1)轴(图4)上的FA1和FB1的投影。通过将动力学基本原理应用于连杆(b1),并将方程投影到不同轴上,我们可以得到以下方程:
——————————————(6)
———————————————(7)
——————————————(8)
3.2.2,连杆(b1)所对应活塞的情况
通过将活塞与系统隔离,如图4所示,并应用动力学的基本原理,我们获得:————————————————(9)
FB1是连杆在活塞上的作用,N是缸体在活塞上的作用(夹套的反作用力)。 P是所产生的燃烧气体压力,其均匀分布在活塞头上并表示如下:
(10)
其中P(theta;)表示活塞两侧的压差。 Ff是套管和活塞环之间的摩擦力,表示为:
(11)
在(O; X1)上投影公式(9)给出以下等式:——————(12)
关于方程(9)在(O; Y1)上的投影,根据外壳与活塞之间的接触发生与否,推导(N→= N),或相反(N lt;0→N)):(13)
方程组(6,7,8,12,13,13)可根据气体压力P,活塞和气缸之间的摩擦系数来确定以下五个连接力N,XB1,YB1,XA1和YA1 f和曲轴转角theta;。 这些力的表述在附录A中给出。
3.2.3,连接情况(b2)
由图4可确定连杆(b2)上曲柄销的力只是其力的角度不同。力的表达与连杆(b1)相似,只是和被替换为和。 它们的表达分别变为:(14)
和:——————————————————(15)
通过方程(14和15)计算组件XA2和YA2中表示为FA2的连杆(b2)的活塞上的力。 由于是四冲程发动机,其他曲轴销上的力是根据两者之间的相位差来计算的。 对于第二,第三和第四个曲轴销,表达式如下:————————————(16)
图5表示根据曲轴旋转角度theta;,由连杆(b1)施加在曲柄销1上的力的演变。
在进气压缩(0到360°之间)和排气(540°和720°之间)过程中,连杆(b1)施加在曲柄销1(YA1)上的力的分量变化为正弦曲线。在燃烧和膨胀过程中(360o和540o之间),它会变为非谐波。 对于组件(XA1),其变化接近正弦曲线。
3.2.4,发动机扭矩研究
根据定义,发动机扭矩是曲柄销上的连杆垂直于曲柄销施加的力的乘积,其半径R =活塞行程/ 2。 考虑到连杆(b1)与缸体轴线相关,并与曲柄销(图6)相关联,我们计算由连杆(b1)在曲柄销1上产生的转矩(图6):—————————(17)
通过类比,连杆(b2)在曲轴销1上产生的发动机扭矩为:—————————(18)
最后,曲柄销1上的总发动机扭矩在每个瞬间等于由两个连杆产生的扭矩的总和。考虑到两个曲轴销之间的相位差(等式(16)),以相同的方式确定其他曲轴销上的扭矩。图7显示,在进气和压缩过程中(0°和360°之间),由第一气缸产生的发动机扭矩相对较低。而膨胀过程对应于较高的转矩值。这可能是由于气缸中高压气体的燃烧对曲柄销造成了较大的影响。在压缩过程中,扭矩变低。图8(a和b)表现了对应不同曲柄销上曲轴转角的单缸扭矩以及发动机总扭矩的变化函数(每个曲柄销扭矩上的叠加)。
4,轴承及曲轴的建模
在本节中,我们确定轴承对曲轴的反作用力。在本文中,使用流体动力轴承模型。由一个光滑的轴承和在轴承衬套内旋转的轴组成,轴承衬套通过流体膜与轴承分开。在载荷的作用下,轴承衬套的中心与轴不重合,并且在薄膜中存在会聚 - 发散角。轴的旋转驱动会聚楔中的流体并产生与负载相反的压力场并使其平衡。该模型侧重于流体动力学状态,并假设通过轴承的流体流动是等温平层流。图9显示了计算油膜流体动压力的方案。根据图9所示的假设和不可压缩的等粘性流体特性,给出了雷诺方程(Jean,1995):————————————(19)
其中P是润滑油中的压力,theta;和Z分别是圆周和轴向坐标,可表示为:theta;= X / R h是润滑油膜厚度;V =omega;R是轴的线速度;mu;是流体的动态粘度。ε是相对偏心率(ε= e / C),其在0和1之间变化。膜厚可以写为:
————————————————————(20)
其中C是径向间隙并表示为:C = R2-R1。
考虑Stierber和Swift的边界条件,也称雷诺条件,在无限短轴承的情况下,再考虑到Gambel的边界条件,假设压力区域限于油膜的覆盖部分(Jean ,1995)。压力场可以表示如下:——(21)
其中L是轴承的长度(图9)。 C = 0; 1毫米。根据长度与轴承直径之比L / D和作用于轴承上的恒定载荷的无量纲值(Jean,1995)S,计算获得ε的值,定义为以下等式:
————————————————————————(22)
其中W是轴承上的恒定载荷。在本文中,S是由轴承支撑的曲轴的重量。
5,曲轴动态特性的建模和仿真
在本节中,我们通过数值编码为ABAQUS的有限元方法对曲轴的动态特性进行数值研究。
5.1,网格
几何模型已经在CAO软件上开发并导入到有限元分析代码中。网格线采用四面体单元类型(C3D4),包含36.215个节点和149.062个单元。
5.2,加载模型化曲轴
- 曲柄销上的力的正确计算是重要一点的。这些力是通过代表节点的一些力来模拟的,因为这些节点需要做出某些分配假设。在曲柄销上,载荷是曲柄销相对于连杆的反作用力,由第3节中提出的动态特性计算得出。(ii) 曲轴整个体积中施加的惯性旋转力。 (iii) 飞轮上的阻力转矩。 (iv) 由轴承 - 曲轴边界条件产生的油膜的流体动压力。图10表示曲轴上的网格和施加的载荷。对于动态计算,我们使用动态隐式方案。表1总结了曲轴的机械性能。
5.3,数值结果
在模拟的数值结果中,我们基本上提取了冯米塞斯等效应力。这些结果使我们能够分析循环载荷下的疲劳(通过使用von Mise)我们可以观察到波动,就像任何部件随时间推移而受到各种应力的情况一样。在计算实践中,这些波动是正弦模型化的。此时的应力最大值为46 MPa(图12),该值仍明显低于曲轴材料的屈服应力:Re = 870 MPa。
5.4,疲劳验证
如第1部分所述,本节的目的是确定
全文共10721字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[9404],资料为PDF文档或Word文档,PDF文档可免费转换为Word


