研究柴油机电磁阀喷射速率的一种现象学模拟方法
Yves Compera, Bernhard Penkert, and Georg Wachtmeister
Technical University of Munich
2016-01-2232 Published 10/17/2016
DOI:SAE Technical Paper 2016-01-2232, 2016, doi:10.4271/2016-01-2232
摘要
本文介绍了一种基于喷射阀性能参数和工作指标估算柴油机电磁喷射阀喷射速率的现象学半经验仿真模型。在这种模型中,近似喷射速率被用作模型的前期输入数据,用以模拟放热速率。该模型包括代数关系、偏离运动方程和守恒微分方程,它通过对模型子单元分解研究,描述了电磁喷射阀的工作特征。电磁阀工作的特征过程及其假设是通过子模块的假设一步步成立。此外,模型喷射速率的仿真结果将于与实验结果进行相比,作为电磁喷射阀参数选择的参考依据。
前语
在柴油机模型的性能参数设置不断提升的大背景下,柴油机零维仿真引擎的开发对于柴油机发展过程而言至关重要。由于大多数柴油机燃烧模型是基于燃油喷射质量而开发出来,故需要一种精确的方法来确定喷射速率,而基于当前由Chmela[22],Barba[3],Eilts[9]等人提出的燃烧模型,可以得到最佳的引擎设计方案用以降低成本或调整模型的燃烧过程。
最近的文献提出了一些用于柴油机燃油喷射系统建模与动态仿真的分析模型,大部分是基于守恒方程通过定义管道内流动状态来描述各机械部件的运动状态。其中关键的一点在于模型中子方程的解法,有些解法采用有限差分方案,如[17],[4],[24],[19]等,但在特征方程中能发现一些有效的解决方法,例如, Wylie.[28],Matsuoka.[20],goyal.[11],Arcoumanis.Fairbrother.[1].Gullaksen.[13]等。其他一些正在开发的模型[29].[16].[2].[7].[9].[15].考虑到在燃油喷射系统或空穴中出现的压力波\瞬态传播现象,因此需要更广泛的仿真研究与计算来得到精确的结构参数。电磁喷射系统制造商通常关注当前使用的母型电磁阀的结构性质,因此我们可以根据母型电磁阀结构来进行模型的优化。本文旨在于将喷射速率作为常见的柴油机热释放速率零维仿真模型的重要输入参数,从而生成一个基于负载和转速的ROHR模型。在实验台上,负载由喷射信号电流的设置量决定,由此可得到喷射质量,同时也要考虑共轨管压力。在共轨压力和一定的喷射系统结构参数确定的情况下,当施加一个目标载荷时,所需要的开启电磁喷射阀电流由ECU中存储的MAP图决定。除此之外,模型中设置的燃油喷射速率对ROHR模型结果的准确性有很大影响。
通常,厂家或用户只会提供很少的有关喷油嘴的参数(孔直径、喷嘴数量、放点电流等),因此,需要一个简化的高精度模型。大部分模型因为缺少细致的结构输入参数而无法得到理想结果,Barba提出了关于喷油速率的简易经验模型[3],模型中喷射速率的polygonal shape由五部分组成,每一部分都需要进行单独的喷射参数调整。此模型的缺点在于过于简单的设置喷射速率,而没有充分考虑共轨压力、孔直径或喷嘴数的影响。因此,本文提出一种基于EMI\EVI的柴油机共轨电磁喷射阀喷射速率现象学仿真方法。EMI被用来将模型校正到特定的喷射系统中。经过EMI校准的模型有喷射速率预测准、计算迅速、适应性好等优点。本文的第一部分提出了对所选方法的总体性叙述,接下来将会有对于所建立模型的详细叙述,包括控制室中守恒方程的基本组成、针阀升程运动的描述、喷嘴压力、喷射质量流量等。此外,还会有关于校准后的模型与实验数据和智能适应参数的描述。最后,通过比对实验数据的方法,将数值模拟结果与实验结果进行比较证明以得到试验后的新开发模型。
技术路线
这种方法的中心思想是在简化条件下定义设定工作工况与喷射系统主要结构参数间的边界情况,即用简化的假设逼近复杂的物理现象。因此为了描述电磁喷射阀的喷射过程特性,必须将模型模块化并建立紧凑的子模块。列出基于曲轴转角分辨率的代数方程和微分方程(偏离方程和守恒方程),再依据经验公式找出其他物理量之间的关系,最后使用EMI进行验证和优化,而在一些特定的子模块中则需要做出一些假设。Wloka[27]描述了特定结构参数和空穴作用对于燃烧过程和放热速率的影响,但这种影响分析却无法得到确切的结果,因为当空穴作用发生时,空腔内充满了蒸发的流体,这会导致当地声速和体积模量的降低。Wloka还发现了HE Rounding对模型的敏感影响。这种模型甚至能超过一些经典的液压仿真模型,例如Schwarzmuuml;ller [23]。
下面列出一些模型的假设状况:
1.燃油温度保持恒定
2.不考虑管道流体流动影响,不考虑机械部分的动力学影响
3.用流量系数修正空穴作用
4.燃油供给压力恒定
5.阻尼和输出阀流量恒定
6.共轨压力恒定
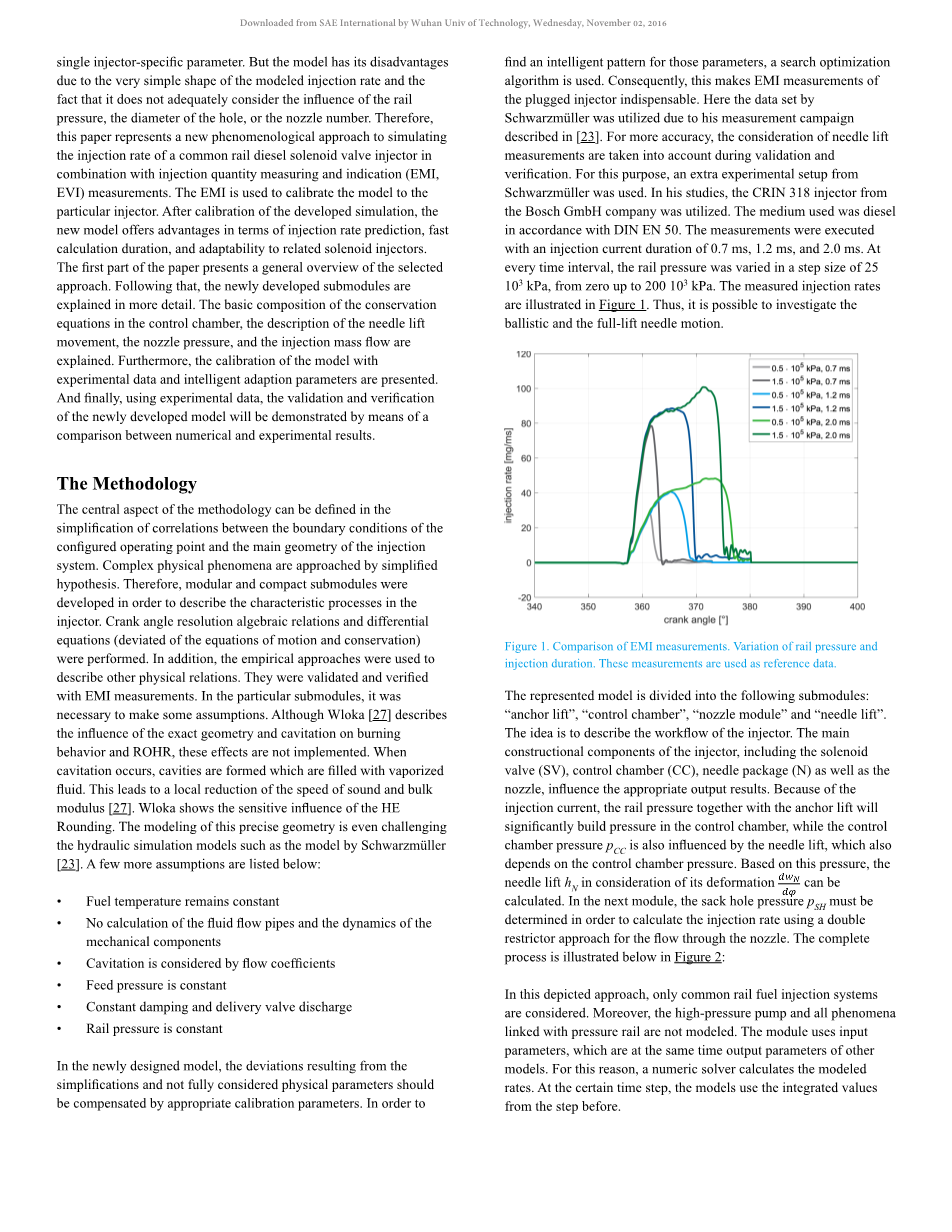
在此模型中,因为简化过程和未充分考虑物理参数的原因而导致的偏差应该通过适当的参数校准来进行补偿修正。应当编写使用优化算法来确定特定的结构参数,因此柱塞泵的EMI方法是必不可少的。Schwarzmuuml;ller在[23]中的测量方法将为本文所用,为了得到更精确的结果,将在检验及模型修正过程中考虑针阀升降测量的影响,正因如此将使用Schwarzmuuml;ller所使用方法中的额外实验装置。在他所进行的试验中,使用的是Bosch GmbH公司的CRIN318电磁喷射阀,燃油符合DIN EN 50标准。电磁喷射阀工作持续时间分别为0.7ms,1.2ms,2.0ms,在每个间隔内共轨压力上升25*1000kPa,从0上升至200*1000kPa。测得燃油喷射速率如图一。由此可得针阀运动状态。
将此模型分为以下几个子模块:lsquo;电磁阀模块rsquo;、lsquo;控制室控制室模块rsquo;、lsquo;喷嘴模块rsquo;、lsquo;阀针运动模块rsquo;,用以描述喷射系统的工作流程。喷油系统的主要结构部件包括电磁阀(SV)、控制腔(CC)、针阀体(N)以及喷嘴等,它们影响相应的输出结果。因为喷射喷射系统内燃油的流动,在电磁阀接通时,共轨管道将在控制室中建立压力,而控制室压力 也受到针阀升程影响,针阀升程同样也取决于控制室压力。基于此压力之下,考虑针阀变形能够计算针阀升程。而在下一个子模块中,为计算喷射速率必须使用双限流方法计算喷嘴的流动速率以及针阀腔压力了 。完整的过程如图2所示。
在此模型中,只有共轨燃油喷射模块被考虑到,高压泵和与压力轨有关的部分未被涉及到。每一个子模型所使用的输入参数是别的子模型同步输出的参数,故需要数值解法来计算建模速度。在一个时间步长内,模型所使用的积分值是此时间步长前的数值。
电磁阀启动模型
由初始输入的控制电流参数计算燃油喷射速率,接下来将介绍一个简单而有效的计算模拟电磁阀启动的方法。在电磁阀不工作时,磁力和气门弹簧恢复力相平衡,但是也要考虑因摩擦和控制室出口泄露而产生变化的受力情况,详见[9].这些影响因素在这个一维模型中被忽略了,因为有类似磁阻、摩擦效率等未知参数。在输出控制电流后,可以将电磁阀工作情形分为三个阶段,启动,近似于一阶线性的电磁阀升程运动,从升压到保持电磁阀开启状态间的过渡阶段。在电磁阀稳定开启阶段内,阀芯处于工作位置,且在整个工作阶段内保持不动。此时,假设对应的电磁阀开启力与控制室出口处横截面积成正比,则横截面积不收到电磁阀工作情况的影响。有效流通面积由对应针阀升程和流量系数决定,流量系数在0到1之间变化,根据[1]可将其设置为0.6.由此,控制室内节流量与电磁力可产生以下方程。
假设对应的电磁阀升程为1,则联立最大升程与升程之间的关系,此时可消去方程中的节流面积
在电磁阀控制开启及关闭阶段之间,假设控制电流相同,则对应的电磁阀升程图是一个梯形。因为控制电流的增加斜率决定电磁阀阀针的启动速率,没有考虑之间产生的系统延迟, 所以系统在这一部分的延迟被忽略。基于控制电流的阀针运动情况如图三
通过模拟控制电流与针阀升程的对比来看,虽然模型是经过简化的简易模型,但是能够只使用低反馈电流值而充分评估电磁阀的电流及其相应的伺服机构。
阀针模型
主体(图四)是由阀针和控制柱塞所耦合而成的一个系统。两者之间没有相对运动。
模型中最重要的参数是控制室压力和喷射腔压力,他们由各自的模块决定。阀针背压与控制室压力相作用,背压由针阀腔恒定压力和由喷射腔压力引起的针尖压力组成。在针阀腔内,压力作用在压力肩上。由此得阀针运动方程3
阀针边缘不受到因静压力而产生的载荷,不会产生针对弹簧弹力和阀门启动力的阻力,因为其产生的阻力经过长距离的传播发生了剧烈的衰减。电磁力作用于阀针孔横截面积上,和作用于阀针肩部的力是同一性质,但是阀针边缘的力具有瞬态性质,这是因为通过针座的节流流量在不断发生变化。压力不断变化是因为阀芯内压力差和针座面积在不断发生变化,针座面积减小时压力也减小,恒定的结构间隙面积变大。但是,在实际的流道相交位置会发生流体压缩效应,在流动过程中因为空间增大的流体汇集效应会导致压力增加,可根据Jungemann[15]近似计算合力。针阀腔中承受有效压力的面积将随着横截面积变化而变化,因此将喷射面积乘以放大系数。因此可将被考虑的因素转化为针阀轴向受力,从而转化为针阀运动情况。液体流动对轴向力的影响与其他力如弹簧力和控制腔压力相比太弱,所以忽略不计。在大多数建立的模型中,各种力的平衡精确计算无法得到,主要是由于缺少结构输入参数(针肩几何参数)。因此,用放大系数代替变化的针阀受力。使用放大系数这种方法,可以直接模拟喷嘴压力的变化量,从而模拟与阀针升降相匹配的实验参考量。本文中实验参考量取放大系数为1.35,在共轨压力和针阀升程变化时保持此值不变。因为高灵敏度的不同仿真模块之间的相互作用,模型中每一个参数变化都会导致针阀升程改变,因此参数成为阀针升程模型中的标准化参数。阀针质量、弹簧预紧力、弹簧刚度在数值计算模型[23]中有提及。控制柱塞的质量约为阀针质量的两倍,但是对于整个模型而言,柱塞质量的影响很小,故这个假设是成立的。本文中阻尼常数由[9]决定。由于阀针运动速度低,与液压力和弹簧弹力相比,运动阻尼将不被优先考虑。除此之外,燃油的重量通常会被忽略。可得以下方程:
忽略悬浮作用和液体阻尼的影响,该方程可以简化。通过广泛有效的分析验证,即使阻尼常数很大仍旧满足此关系。参数能够适应阀针工作区域,因此可被用来描述不同结构参数的喷射系统的阀针。
本文所介绍的一般方法均可用于此模型中。将阀针加速度积分可得到阀针升程,即可确定阀针环隙面积。此外,阀针升程和阀针加速度还可用于计算控制室压力曲线(见下章)。从而得到控制柱塞运动对于控制室压力的影响。
考虑到阀针是在静态载荷下的线性弹性模型,且在针阀系统外部会形成压力平衡,这有可能导致阀针的变形。在[23]、[9]、[5]的描述中,当控制室未加载时阀针不存在形变,则可以用线性方程描述这个过程,则可基于针阀和控制柱的参数结构用偏微分方程描述相应的阀针变形过程。阀针分析过程首先是平衡情况下的弹簧力取决去当前阀针变形量。
又有如下关系
运动偏微分方程如下
如果阀针处于静止状态,针座将受到反作用力,对这两个组件定义它们的平均横截面面积并假设其质量均匀。和[1]不同,外部的弹簧力和所有的阻尼效果都被忽略,因为和其他的外部力相比时可以被忽略,简化机械系统如图五。假设恒定的轴向力,可得控制室压力。因此微分方程的变化量为零。
由控制室压力计算外部力,控制室压力随阀针升降而变化。控制室压力值将在接下来进行探讨。阀针的最大形变与共轨压力有关。
则方程8可以简化为:
控制室内压力曲线
控制室的压力曲线可以基于近似电磁阀开度来进行描述。电磁阀开度作为控制参数。控制室内部各种压力的大小关系决定阀针针的运动情况。压力大小情况可以根据连续性方程来进行建模。因此,有必要确定控制室进口的流量和控制柱塞(CP)的运动情况(见图6)。共轨压力近似假定与控制室入口相同。控制室出口压力由处于100到600 kPa压力范围内的回流燃油道决定。控制室流动速率可以由方程(10)描述。用流量系数描述控制室入口的节流损失。用有效出口面积(见公式(1))表示出口损失,而控制室内压力情况和流量变化取决于具体流动情况。为了进行精确的压力调节,控制室出口直径应大于入口直径,比值设置为1.2。
控制柱塞的运动情况直接决定阀针的瞬时运动状态,即控制室的体积取决于阀针的位置。根据[11]计算最大体积。
根据喷射模型[23]将该方程进行数据验证(在AVL BOOST HYDSIM模型中)。由于控制室与出口之间的高压力差,出口流量值越来越高,直到电磁阀完全打开。由于
全文共15147字,剩余内容已隐藏,支付完成后下载完整资料

英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[145125],资料为PDF文档或Word文档,PDF文档可免费转换为Word


