英语原文共 13 页，剩余内容已隐藏，支付完成后下载完整资料

基于ANYSY-CFX的卧式浆流管道的流体力学模拟

Kalekudithi Ekambara, R. Sean Sanders, K. Nandakumar, Jacob H. Masliyah

阿尔伯塔大学化学与材料工程系，加拿大埃特蒙顿，AB，T6G 2G6

水平固 - 液（浆流）管道流动的规律是使用基于颗粒流动动力学理论的瞬态三维（3D）流体动力学模型预测的。利用商业CFD软件包ANSYS-CFX所计算出的流体动力学（CFD）模拟结果比对了大量实验性数据，从中获取了我们所需要的数据。通过模拟来研究原位固体体积浓度（8〜45％），粒径（90〜500mu;m），混合物速度（1.5〜5.5m/s）和管径（50〜500mm）对位置，时间-平均固体浓度分布，颗粒和液体速度分布以及摩擦压力损失的影响。模型预测与实验结果具有良好的一致性。实验和模拟结果表明，颗粒在垂直平面中不对称分布，不对称程度随着颗粒尺寸的增加而增加。一旦颗粒足够大，浓度曲线只取决于原位固体体积分数。本CFD模型不需要实验确定的浆料管道流量数据进行参数调整，因此可以认为优于常用的基于相关的经验模型。

1.简介

固- 液（浆料）输送已经用于诸如煤，矿物精矿和尾矿的长距离输送长达数十年。在过去的20年中，阿尔伯塔北部的油砂业已成为世界上浆料运输最频繁的用户之一。油砂矿石的稠密粗颗粒浆料通过管道从采矿场运输到采掘设施。管道输送还用于将废尾渣运送到最终处置场。在大多数情况下，浆料管道比其他散装物料处理方法更节能，并且操作和维护成本更低。此外，涉及浆液流动的操作在许多其他行业中发挥了重要作用，包括制药制造，纳米制造和石油炼制。

大多数浆流的工程模型集中在预测粗颗粒，“沉降”浆液的摩擦压力损失和最小操作速度（或“沉积速度”）的能力。有很多这种类型的模型在预测上述参数方面具有不同程度的成功。如下所述，很多这样的模型是具有现象性的，意味着需要一些经验导出的参数或关系。另外，这些模型倾向于仅提供宏观参数，例如，对于窄尺寸浆料的摩擦压降，沉积速度和输送固体体积分数。然而，许多工业浆料包含一系列不同的粒径。这些颗粒在流体中不同位置和速度都将严重影响管道操作。如果要提高对介观过程（例如，管道磨损，颗粒磨损或集聚）的理解，那么知道这些参数随管位置的变化是关键的。此外，更复杂的三相或四相流的分析将需要提供颗粒浓度和速度的局部值的模型。最后，在更复杂的几何形状（泵，水力旋流器，混合罐）中对浓度和速度分布的准确预测将需要发展和验证机械计算模型。

随着计算能力的提高，在建模流体力学中计算流体动力学（CFD）将成为一个非常有前途的新的工具。虽然它现在是单相流的标准工具，但它正处于多相系统的开发阶段。需要开展工作使CFD适用于泥浆管道的建模和扩大。考虑到这个问题的现状，已经将基于颗粒流动力学理论的综合三维计算流体动力学（CFD）模型在水平浆料管道流动中付诸实施。该模型的动力学理论组分是关键的，因为它考虑了颗粒之间和颗粒与悬浮液相之间相互作用的影响。进行模拟来研究固体体积分数，粒径，混合物速度和管径对颗粒浓度和液体速度的空间变化以及摩擦压力损失的影响。在大范围的管道操作条件下，将模型预测与现有实验数据进行比较：平均固体浓度为8〜45％（体积），均匀粒径为90〜500mu;m，混合物速度为1.5〜5.5m / s，管径为50〜500mm。

图1 水平浆料管线模拟的网格结构

表1 流体力学模拟建模的实验数据

在讨论计算方法和模拟结果之前，先简要回顾一下这方面以前的工作。

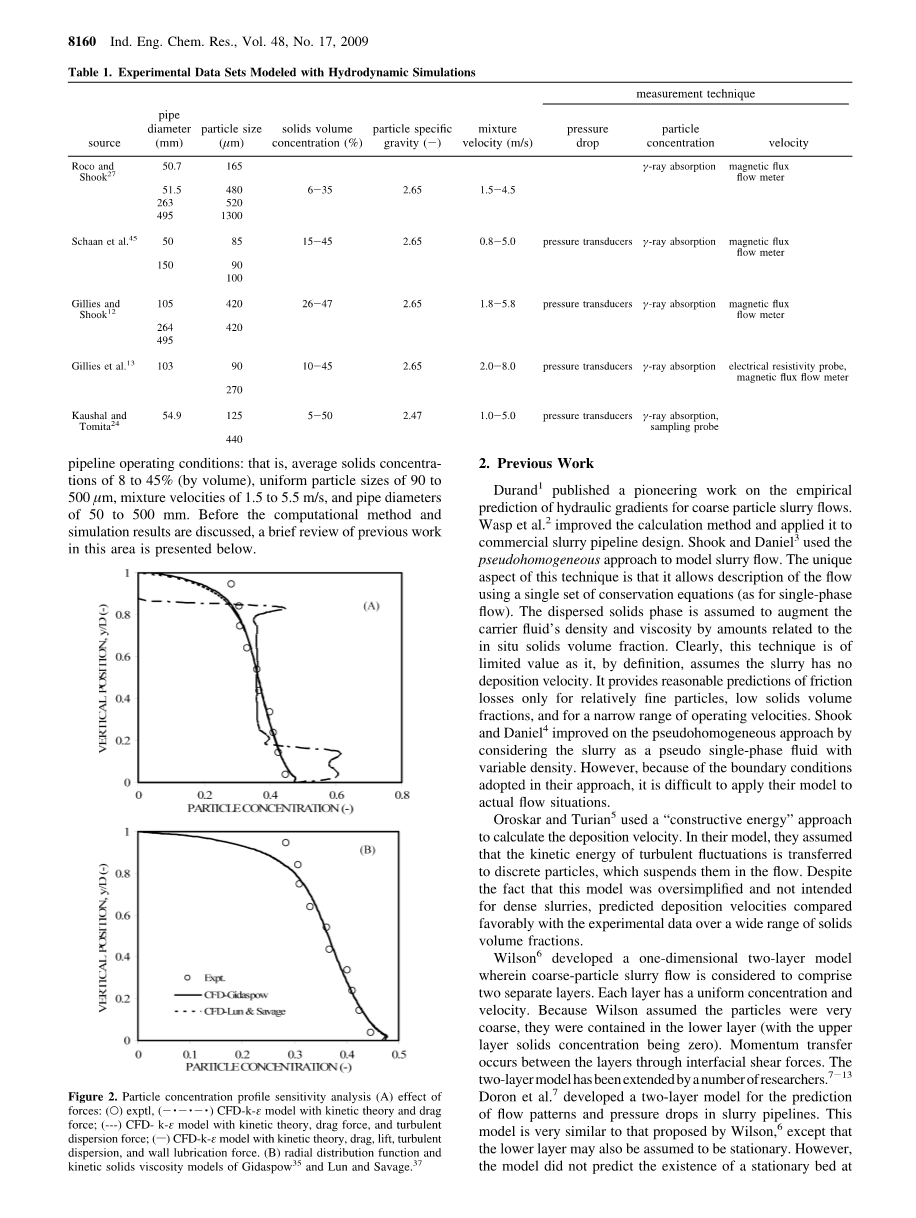
图2. 粒子浓度梯度灵敏度分析。（A）力的影响：（○）实验性，（ -·-·-·）CFD-k-ε模型动力学理论和阻力；（---）CFD-k-ε模型，动力学理论，拖曳力和湍散弥散力; （—）具有动力学理论，阻力，升力，湍流扩散和壁润滑力的CFD-k-ε模型。（B）Gidaspow[35]、Lun和Savage[37]的径向分布函数和动力学固体粘度模型。

2.前期工作

Durand[1]发表了关于粗颗粒浆液流动的水力梯度的经验预测的开创性工作。Wasp等人²改进了计算方法，并将其应用于商业浆料管道设计。Shook和Daniel[3]使用假均匀方法来模拟浆液流。这种技术的独特之处在于它允许使用单组保守方程（对于单相流）描述流动。假定分散的固体相通过与原位固体体积分数相关的量增加载体流体的密度和粘度。显然，这种技术是有局限性的，因为它假设浆料没有沉积速度。它只对相对精细的颗粒，低固体体积分数和狭窄的操作速度范围提供了合理的摩擦损失预测。Shook和Daniel[4]通过将浆料视为具有可变密度的假单相流体改进了假均匀方法。然而，由于他们的方法中采用的边界条件，很难将其模型应用于实际流动情况。

Oroskar和Turian[5]使用“建设性能量”方法计算沉积速度。在他们的模型中，他们认为湍流波动的动能被转移到离散的颗粒，它们悬浮在流体中。 尽管事实上这个模型过于简单，并且不打算用于稠密浆料，但是预测的沉积速度与实验数据在宽范围的固体体积分数上相比是有利的。

Wilson[6]开发了一维双层模型，其中粗颗粒浆流被认为包括两个单独的层。每层具有均匀的浓度和速度。因为Wilson认为颗粒非常粗，所以它们被包含在下层中（上层固体浓度为零）。通过界面剪切力在层之间发生动量转移。这些双层模型通过研究人员的数量来扩展。Doron等人[7]开发了一种用于预测泥浆管道流动模式和压力降的双层模型。该模型与Wilson[6]提出的模型非常相似，除了下层也可以假定为静止的。然而，该模型没有预测在低流量下固定基体的存在，这也降低了压降预测的可靠性。Wilson和Pugh[8]开发了异质浆液流的分散力模型，这扩展了原Wilson模型的适用性，因为它考虑了由液体湍流悬浮的颗粒以及提供接触负载（库仑）摩擦的颗粒。该模型用于预测粒子浓度和速度剖面，与实验测量很好地一致。

Nassehi和Khan[9]开发了一种用于确定两层浆料流层之间的滑动特性的数值方法，但没有报道实验结果与它们的数值解之间的比较。

图3. 和的预测和实验测定[13]的浓度曲线的比较：(A), (B),(C), (D), (E), (F) .

毫无疑问，两层模型最常用的版本是由Gillies和同事开发的SRC模型[10-13]。SRC两层模型提供压力梯度和沉积速度的预测作为粒径，管径，固体体积分数和混合物速度的函数。这种模型是“半机械的”，因为管道直径对管道摩擦损失的影响是机械地指定的（即不依赖于任何经验确定的系数）。其包含的半经验系数基于在萨斯喀彻温研究委员会管道流动技术中心进行的数千个控制实验。由于最佳管道速度通常接近沉积速度（Vc），因此在模型中包含的大部分数据是在刚好大于沉积速度（Vc le;Vle;1.3Vc）的混合物速度下获得的。

Doron和Barnea[14]将两层建模方法扩展到水平管道中的泥浆流的三层模型。他们的模型考虑了分散层的存在，其夹在悬浮层和床之间。认为分散层具有比悬浮层更高的浓度梯度。在固体颗粒和流体之间假定不滑动条件，这是合理的，当流体在水平或近水平配置。模型预测显示与实验数据令人满意的一致性。Doron和Barnea也使用了一个三层模型来绘制流图模式图，可以用来表示流动模式（基本上就是流动异质性程度）。他们确定了所谓的“流动模式”之间的过渡线，并将这些结果与实验数据进行比较。Ramadan等人还开发了一个三层实体模型，并用于模拟倾斜通道中的浆料输送。将模型预测与实验进行比较，清楚地证明了该模型的局限性。

图4. 和的预测和实验测定[13]的浓度曲线的比较：(A), (B),(C), (D).

还存在对淤浆流动模型的单独（但相关）方法，其中一维Schmidt-Rouse方程[11]（或等价物;参见Hunt[17]）用于将颗粒沉降速率与湍流交换速率相关联，固体涡流扩散性，

其中是对位置而言的时间—平均固体体积分数，是终端颗粒沉降速度，是管道中的垂直位置。Karabelas[18]开发了一个基于这个公式预测粒子浓度特性的经验模型。Kaushal和他的同事[19-24]基于Karabelas[18]的工作开发了一个扩散模型，他们提出了粗颗粒浆液流固体扩散率的修正。他们构造了经验相关性，确定固体扩散率与液体涡流扩散率的比率。它们的功能表明固体扩散率随着固体浓度的增加而增加。然而，它没有考虑固体扩散性对颗粒尺寸和管道雷诺数[25]的显着依赖。他们还将其压降数据与修改的Wasp模型[26]进行了比较，考虑了气体浓度对无量纲固体扩散率[20]的影响，在较高流速下有良好的一致性;然而，在沉积速度附近的流速下，偏差是明显的。

Roco和Shook[27-29]为稠浆管道流体开发了类似的模型。他们认为浆料是牛顿流体，其特征在于使用混合物的密度和粘度。它们通过在Navier-Stokes方程中引入流动的湍流性质，Navier-Stokes方程是表征湍流粘度的经验项。使用类似于上述的半经验扩散方程确定颗粒浓度分布。将模型预测与小于35％的固体体积分数的实验数据进行比较。该模型在较高的固体体积浓度下不可靠。另外，Rocoandco工人[30,31]修改了湍流模型，并使用较高阶相关性以获得更好的涡流粘度估计。Roco和Mahadevan[31]使用单方程动能模型来计算湍流粘度。该模型提供了良好的预测；不过，它包含许多经验参数。

图5. 和的预测和实验测定[45]的浓度曲线的比较：(A)V, (B).

Gillies和Shook[11]显示了这种类型的模型的最显着的限制。当颗粒尺寸足够大使得颗粒不能被流体湍流支撑时不适用，当时发生流体湍流，其中是摩擦速度（）。 随着粒径（和）增加，浓度分布具有明显不同的形状，变得很大程度上依赖于局部浓度并且几乎不依赖于混合物速度（或流体湍流水平）。

当颗粒直径相对较大并且混合物速度较大时，已经进行了从管底部向上的颗粒浓度的局部最大值的大量观察[3,11,24,32,33] 。WilsonandSellgren[32,33]证明了该效应是结果在某些粗颗粒浆液流中发生的近壁升力。最近，Kaushal和Tomita[24]在55mm管道回路中用两种窄尺寸玻璃珠（0.125和0.44mm）进行实验。这些结果清楚地表明了近壁提升力对含有粗颗粒的浆料的浓度分布和摩擦压力梯度的重要性。这些研究人员确认了Wilson和Sellgren的许多研究结果：最明显的是，较小的

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[141169]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 9000吨供油船机舱设备选型与热平衡分析外文翻译资料
• 沿海高速客船机舱设备选型及经济性分析外文翻译资料
• 海.上溢油应急技术外文翻译资料
• 可变压缩比柴油发动机的效率和生态特征外文翻译资料
• 高速船 第4部分 船舶系统和设备外文翻译资料
• 14平衡常数 外文翻译资料
• 敞水中空化螺旋桨和喷嘴式全 回转推进器的CFD研究外文翻译资料
• 生物燃料及其二元(柴油-生物柴油)和三元(乙醇生物柴 油-柴油)混合燃料在内燃机减排上的作用外文翻译资料
• 游轮发电厂优化和比较分析外文翻译资料
• 内燃机最优放热率计算外文翻译资料