英语原文共 16 页
基于新的进化算法对凸轮—滚柱传动机构的优化设计
摘要:如今,凸轮机构作为一精密机构的替代品在工业上被广泛应用,这使得其优化设计成为接触力学中一个非常热门的问题。本文提出了一种改进的自适应差分进化算法(MADE),用于偏置平移滚子从动式凸轮机构的多目标优化。并以优化凸轮的最小阻力、最大效率和最大强度阻力为目标,研究了优化过程。在优化过程中,为提高机构的设计质量,更多的几何参数和更多的设计约束包含在问题模型中。为了验证所提出的算法,还利用其去解决三个工程设计问题。这些问题的仿真结果表明:与现有的各种优化方法相比,该算法具有有效性和鲁棒性。最后,通过算例得到的优化结果为凸轮机构总成提供了非常有用的决策依据。
关键词:凸轮机构;滚子从动式;约束问题优化;差分进化算法
1.引言
凸轮机构是如今现代化机械中最简单,最重要的机构之一。它广泛应用于机械装置和机器,特别是自动化机械装置和机器,如印刷机,纺织机,齿轮加工机器,螺丝机和汽车发动机。然而,该机构的主要缺点是凸轮和从动件之间的直接接触。这种接触由于摩擦而在凸轮上引起负载转矩,这导致在两个接触部分中有一部分能量将转化为热量而损失掉。滚子通过减小摩擦来提高系统的传动效率,但同时增加了机构的阻力。因此,凸轮尺寸最小化通常是凸轮机构设计过程中的主要目标。另外,高系统性能的要求意味着考虑凸轮阻力和凸轮轮廓以提高所需的运动精度并因此优化机构的稳健性。
在凸轮及其从动件设计领域,已有很多研究报道。但是,这些研究大部分都没有详细论述机构的设计。因此,在该领域需要更多的研究,特别是随着计算技术和优化方法的快速发展。在过去的几十年中,凸轮机构的最佳设计已成为许多研究出版物的主题,其中考虑了各种方法。基于迭代数值方法,Terauchi和El-Shakery 使用Regula-Falsi和Newton-Raphson方法在接触应力约束下最小化凸轮滚子从动件机构的尺寸。Bouzakis等采用非线性规划方法,基于机构的结构和功能要求来优化凸轮的尺寸。对于约束的处理,其采用了外点惩罚函数法。Carra等人研究了具有负半径滚子从动件的凸轮机构总成,通过数值分析法实现压力角最小化。在他们的工作中,他们研究并讨论了不同变量对底切和压力角问题的影响。
一些更先进的技术,如遗传算法(GA)已被应用于凸轮机构优化设计。 Lampinen 使用遗传算法进行凸轮形状初步设计和凸轮操纵机构的优化。Tsiafis等人提出了一种多目标遗传算法,用于得到具有平移滚子从动件的凸轮机构的最佳设计参数。这种优化方法用于找到关于上述目标函数的一组Pareto最优解。 该作者还采用了遗传算法来优化一种带平面平移从动件的盘形凸轮机构的设计参数。作者已经考虑了三个目标。后来,Flores提出一种算法,用于优化带有偏心平移滚子从动件的盘形凸轮机构。他使用MATLAB的fmincon函数来解决这个问题。
最近,Hidalgo-Martinez等人开发一种优化程序,以研究型线基于贝塞尔曲线建立的负半径滚子从动件凸轮机构。同样地,Hidalgo-Martinez和Sanmiguel-Rojas也基于贝塞尔曲线,以最小化滑动速度为目标,研究了带单平面和双平面平移从动件凸轮机构的合成。他们论述了该参数对这类凸轮机构的摩擦损失和疲劳寿命的影响。 最近,Jana和Bhattacharjee开发了一种多目标遗传算法,用来解决具有简谐和双谐波轮廓的凸轮机构的设计优化问题。他们旨在优化旋转角度,从动件最大推力和及其对应的角度这些运动学变量。
本文的主要目的是通过使用一种称为MADE的新进化算法,基于此优化方法合成具有偏心平移滚子从动件的凸轮机构。与以前的研究不同,本文在优化过程中考虑更多的几何参数和设计约束,来改善凸轮机构的设计质量。优化问题基于最小化凸轮尺寸,最大化机械效率,以及最大化凸轮机构阻力三个目标建立。通过优化三杆约束工程设计问题,包括三杆桁架设计,弹簧设计和焊接梁设计等问题,验证了该算法的有效性。
因此,下文分章节描述了:优化问题的制定,目标函数,约束和设计变量。在第3节中,作者简要介绍了经典DE算法的不同步骤。在第4节中介绍了开发的MADE算法,并在第5节中进行了验证。在第6节中,提供了一个应用示例,用于讨论整个工作中采用的主要假设和程序。 最后,结论在第7节中给出。
2凸轮机构的问题建模
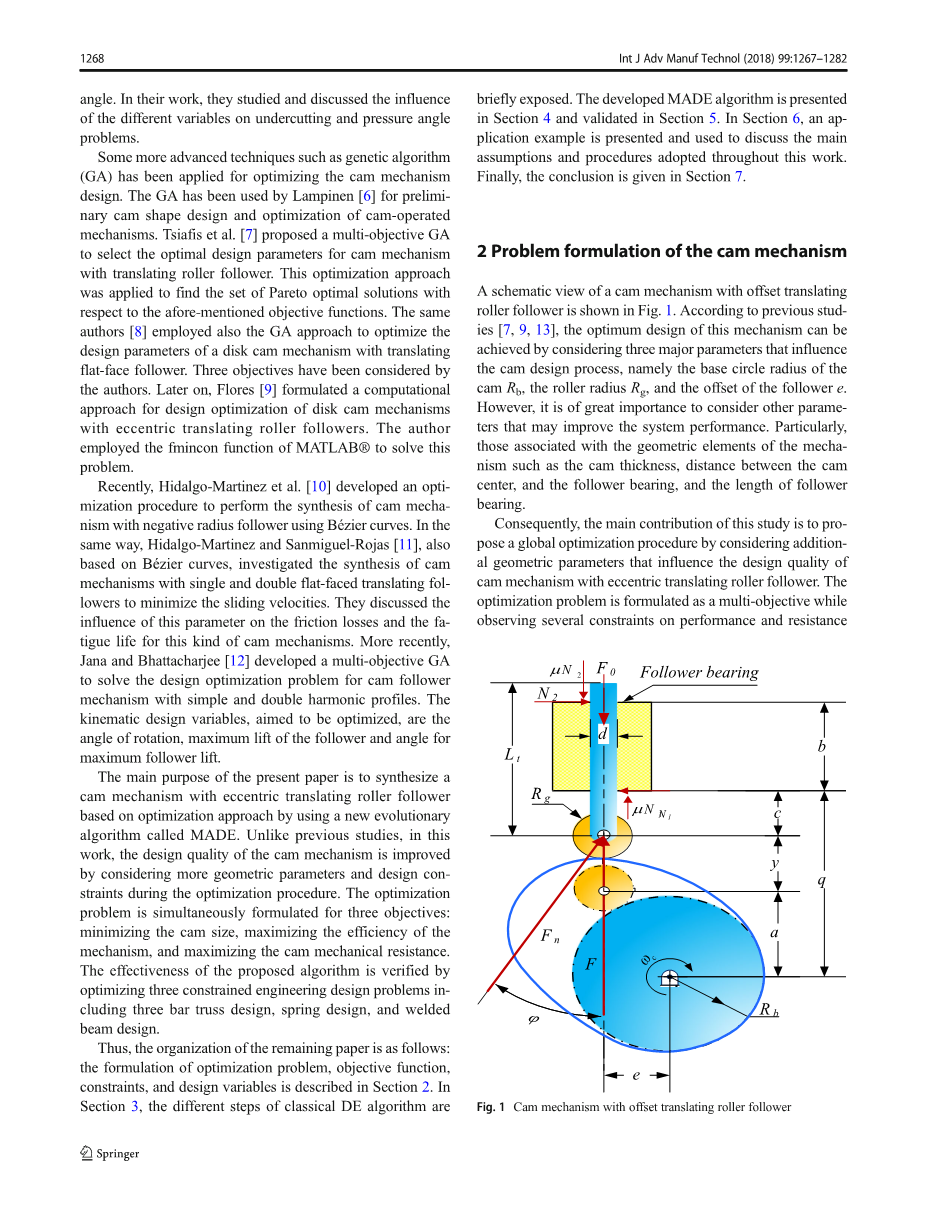
图1显示了带偏置式平移滚子从动件的凸轮机构的示意图。根据之前的研究,考虑改变影响凸轮设计的三个主要参数:凸轮Rb的基圆半径,滚子半径Rg和从动件e的偏移,可以实现该机构的优化设计。但是,考虑可以提高系统性能的其他参数更加重要,特别是与机构的几素相关的那些,例如凸轮厚度,凸轮中心和从动轴承之间的距离,以及从动轴承的长度。
图一.带偏置平移滚子从动件的凸轮机构
因此,本研究的主要工作是:通过考虑影响带偏置平移滚子从动件的凸轮机构设计质量的其它几何参数,提出全局优化程序。优化问题基于多优化目标,并考虑性能,阻力值以及几何条件等约束条件建立。在下文中,将详细说明目标函数,约束和设计变量。
2.1目标函数
偏置平移滚子从动式凸轮机构以凸轮的最小阻力、最大效率和最大强度阻力为目标,在数学上,目标函数可以表示为:
(1)
其中beta;i(i = 1,2,3)是加权因子基于解决特定问题的目标函数的加权因子,x是设计变量的向量。由式1可知:第一个目标是凸轮尺寸最小化。凸轮尺寸由基圆半径Rb和凸轮t的厚度决定。第二个目标是减小驱动凸轮所需的最大输入扭矩Tmax,这能直接提高机械效率。最后一个目标使凸轮和从动件之间的最大接触应力sigma;Hmax最小化。瞬时输入扭矩给出如下:
(2)
其中F是凸轮作用于滚子从动件上的力,yacute;是对应于凸轮角度变化的从动件位移表达式的一阶导数。
2.2约束条件
上述目标函数有十个约束条件。在本节中,详细给出了每个约束条件。
前两个约束用以简化机构装配(图1):
(3)
(4)
为了确保在从动件的较长停顿期间机构的正确工作,滚子不应接触从动轴承。 因此,应建立以下约束以避免接触:
(5)
其中h是从动件的升程,q是凸轮中心和从动轴承之间的距离。 参数alpha;的计算式为:
(6)
另一方面,在短暂停留期间,从动件高度不应低于轴承高度,以避免外部质量与后者之间的任何接触。约束的数学表达式为:
(7)
如图1示:L是从动件的长度,b是从动件轴承的长度。
为了保证机构的正常工作,对压力角施加了两个约束。如下是上升和下降期间允许的最大值,表示为:
(8)
(9)
压力角表达式如下:
(10)
为了避免底切以及保证机构按要求运动,对型线的曲率半径rho;施加其他两个约束。当凸轮位于凸起位置时,最小曲率半径rho;min应大于或等于滚子半径Rg 。 当凸轮位于凹起位置时,最小曲率半径的绝对值|rho;min | 应该远大于Rg。因此,这两个约束表示如下:
For rho;gt;0 (11)
For rho;lt;0 (12)
其中r是一个正常数,用于控制凸轮凹部的曲率半径的变化。理论型线rho;的曲率半径的计算式为:
(13)
其中y'是关于凸轮角度变化的的从动件位移函数的二阶导数。
为保证凸轮的机械阻力,最大接触应力sigma;Hmax应小于或等于允许的接触应力sigma;HP。该约束的数学表达式为:
(14)
凸轮上的最大接触应力计算式如下:
(15)
其中Fn是凸轮表面和滚子从动件之间的法向力:
(16)
其中P是作用在从动件上的合力。该力是由外部施加的力F0,惯性力Fi和弹力Fs的组成的合力。mu;是从动件与其轴承之间的摩擦系数,C=q-(a y)(图1)。upsilon;1,upsilon;2是泊松系数,E1,E2分别是凸轮和滚子从动件材料的弹性模量。
最后一个约束是系统的机械效率。机械的动力传递应该实现最小的能量损失,能量损失主要是由摩擦力和压力角造成。因此,建立最小能量损失的约束如下:
(17)
瞬时效率由合力P除以从动件上升所需的力F。其表达式可写为:
(18)
2.3设计变量
从问题的表述中可以明显看出,凸轮机构的优化设计受到先前提出设计变量参数的影响,这些参数彼此冲突。当凸轮厚度t增加时,由于接触应力的直接减小,凸轮的阻力得到改善(第三目标)。但与此同时,凸轮尺寸变得更大,这不符合第一个目标。所以有必要选择该参数的最佳值。而且,距离q的减小会使机械效率eta;增加但输入扭矩T减小。这意味着我们对目标函数的第二项优化时,应该遵守约束条件3。另一方面,从动轴承的长度b对输入扭矩和约束g4有一定的影响。并且轴承长度和输入扭矩能直接影响法向力Fn,从而影响接触应力(目标函数的第三项)。
基于以上分析,以六个设计变量建立了凸轮机构设计的最终优化模型。 它们是凸轮基圆半径Rb,滚子半径Rg,从动件偏心距e,凸轮厚度t,凸轮中心与从动轴承之间的距离q,以及从动件轴承长度b。所有设计变量都是连续的。
3差分进化算法的基本步骤
DE算法是Storn和Price首次提出的,它是最有效的进化算法(EAs)之一,用于实参数优化。与其它进化算法一样,DE是基于人口的优化算法。经典的DE算法可以分为四个步骤,即初始化,变异,交叉和选择。在初始化阶段,在每个决策变量(,i=1,..,D and j=1,..,NP.)的可行边界约束内随机创建群体NP。D表示设计变量的数量。
在初始化之后,DE使用突变操作为每个目标变量创建突变变量。DE / rand / 2 / bin策略是最常用的策略,其中bin表示二项式交叉运算符。突变变量可以如下计算:
(19)
其中r1,r2,r3,r4和r5是在[1,...,NP]范围内随机选择的整数索引,它们彼此不同并且也与索引j不同。F1和F2是缩放因子,G表示生成数。
在二项式交叉中,使用目标变量和突变变量生成试验变量
(20)
其中irand是在[1,...,D]中选择的随机整数,randi,j是0到1之间均匀分布的随机数。
在选择这一步,将目标变量与试验变量相比较,根据它们的细度值选择更好进入下一步骤:
(21)
如果满足停止的条件,则终止计算。否则,重复步骤:突变、交叉和选择。
4.改进的自适应差分进化算法
本文所提出的方法可以被认为是自适应混合差分进化(AMDE)的改进版本。 具体来说,AMDE算法被用来选择圆柱形齿轮的最佳几何参数。此外,为避免手动调整突变和交叉值,该方法基于自适应机制jDE。有关AMDE方法的更多详细信息,有兴趣的读者可参考参考文献。
在本文,在选择阶段而不是常规阶段,利用Deb提出的可行点机制的优越性,改善了MADE算法,并提高变量的搜索能力。其中Deb的方法是基于当比较目标变量和试验变量时的三种选择方案。每个标准如下:当两个解在可行区域中时,选择具有更好适应值的解;如果一种解决方案是可行的而另一种解决方案是不可行的,则选取可行的解决方案;当两种解决方案均不可行时,则选择具有小约束违反值的那个。可以注意到,在这项工作中,我们将只处理连续类型的问题。
5.评估MADE的方法
为了评估所提出方法的性能,选择了三个实际的工程优化问题:三杆桁架设计、拉伸弹簧设计和焊接梁设计问题。基准工程设计问题的数学公式见附录。jDE问题的参数如下:初始化过程设置F1 = 0.8,F2 = 0.5,Cr = 0.5,tau;1= 0.5,tau;2= 0.2,tau;3= 0.1。在范围[4D 10D]中选择NP,并在表2中给出函数求值(FE)的结果。此外,对于每个问题,独立运行50次并且提供包括最佳值,平均值,最差值和标准偏差的统计结果。MADE算法在MATLABreg;中实现,优化运行在带2.2 GHz和4 GB RAM内存的PC i5上执行。
最近,通过使用几种方法解决了上述问题。将MADE算法与以下启发式算法进行比较:AMDE,rank-iMDDE,基于改进
资料编号:[3654]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。