
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
基于偏振特性的锂离子电池最优充电方法
摘要:
电池充电变得越来越重要,因为它直接影响电池的性能和安全。本文开发一个通用的在线估计方法-基于阻容(RC)电路模型的充电极化电压来模拟锂离子电池的充电行为。充电电流的影响,初始状态(SOC),初始偏振状态和老化电荷极化电压在时间和SOC领域被广泛定量分析,这也证明了电荷极化电压非线性与这些影响因素有关。在SOC域中,电荷极化电压的变化也用梯度分析方法进行了分析,同时电流,极化电压振幅的拐点和电容状态之间的联系也被基本确定。这可以准确地用来估计电池SOC和极化电压。为了适应电池不同的电容状态阶段,专家提出了一个基于模糊控制的固定极化充电方法。实验结果表明,与传统的恒流-恒压充电方法相比,上述的充电方法在电池温度没有明显升高的前提下显著地减短了充电时间。
关键词:电池充电;固定极化;模糊控制;锂离子电池。
1.介绍
自从锂离子电池充电技术成为电动汽车的重要组成部分,它就被更广泛的研究。传统的充电方法包括电流控制,电压控制和马斯定律。恒流充电是一种被广泛使用的充电的方法:以很小的电流充电以防止电池电压和温度的快速升高。然而这种方法难以配置合适的流速平衡电池充电时间和能力以确保电池安全。在恒压充电中电池以固定电压充电以避免在充电过程的结束阶段电池过载。充电过程的初始电流太高会减短电池的寿命。恒流-恒压充电方式结合了这两种充电方法从而提高了充电表现和安全性。马斯充电方法可以通过“马斯三定理”计算电流来给电池充电,但这是给铅酸蓄电池充电的而非锂离子电池。现代智能充电方法近年来已被报道,包括迷糊控制,蚁群算法,遗传算法等的运用,以提高电池充电的速度(基于智能控制算法设置充电电流轨迹)。在“Search for an optimal rapid charging pattern for lithium-ion batteries using ant colony system algorithm”中,蚁群算法给出了锂离子电池的充电模式;在“A design of a grey-predicted Li-ion battery charge system”中,grey-predicted锂离子电池充电系统被设计出来以取代恒压充电模式;充电器可以增加充电的速度和效率。然而这些都需要极高的成本。
本文介绍了一种基于恒定极化电压的快速充电技术。它提出了一个以模拟锂离子充电的阻容电路模型为基础的广义估计电荷极化电压的方法,然后用线性和非线性的影响因素对极化电压进行了分析。不仅如此,其他影响因素例如电流,电容状态,放置时间,电池的计划电压的降低也被一定程度上考虑。在时间和电容状态领域的极化电压也被考虑;拐点的极化电压,电流和电容状态之间的关系也被考虑进去。最后,本文介绍了建立在电池电容状态和充电电流的电极变化基础上的模糊控制充电算法。算法调整充电电流的接受取决于SOC。这个研究不仅对插电混合动力汽车和纯电动汽车有价值有帮助,也为电动汽车充电设施的设计提供了参考。
2充电极化电压的功能
A.极化电压分析
等效电路模型,神经网络和简化电化学模型在电池领域被广泛应用。“戴维宁”等效电路模型描述了在实验中所用的锂离子电池的充放电行为。在电池模型中,电动势等效电压电源,固有的电导率化学结构及其极化表现
图1:戴维宁电池模型
分别由欧姆电阻和RC电路表征
电势平衡方程如下:
代表电池端电压,代表电池极化电压,代表电阻压降。欧姆电阻是电容状态的功能,它的计算方法在“Identification of dynamic model for
dynamic model for lithium-ion batteries used in hybrid electric vehicles.”中被讨论。正如在“潜在平衡方程”中讨论的,如果电容状态已知,极化电压如下所示:
代表开路电压和SOC之间的功能关系。在指定的时间间隔内开路电压被认为和SOC之间是线性关系,它们的关系如下:
H和B分别代表线性方程的斜率和截距。
在本文中,恒定电流被用来确定开路电压作为SOC的功能;因此,SOC可以被准确地算出,开路电压建立在“Current-pumped battery charger,”基础上可以得出。UR可以通过将电池电流和电阻相乘得到,然后极化电压可以通过 “Multi-step constant-current charging method for an electric vehicle nickel/metal hydride battery with high-energy efficiency and long cycle life,”估计得到。
在本文中,一种可用容量为72AH的 LiMn2O4电池被用来执行这些工作。这些电池通过恒流-恒压方式充电来验证极化电压估算。在实验中,这些电池在空载状态时先以0.3C的恒定电流充电。在冲了5%的电时,充电停止,然后电路保持开路状态2小时,开路电压得到。然后电池以恒压的方式充电直到电池终端电压达到4.2V。开路电压的初始值和终值之间的区别被认为是极化电压的真实值。重复上述步骤,极化电压保持在SOC的5%直到到达100%。
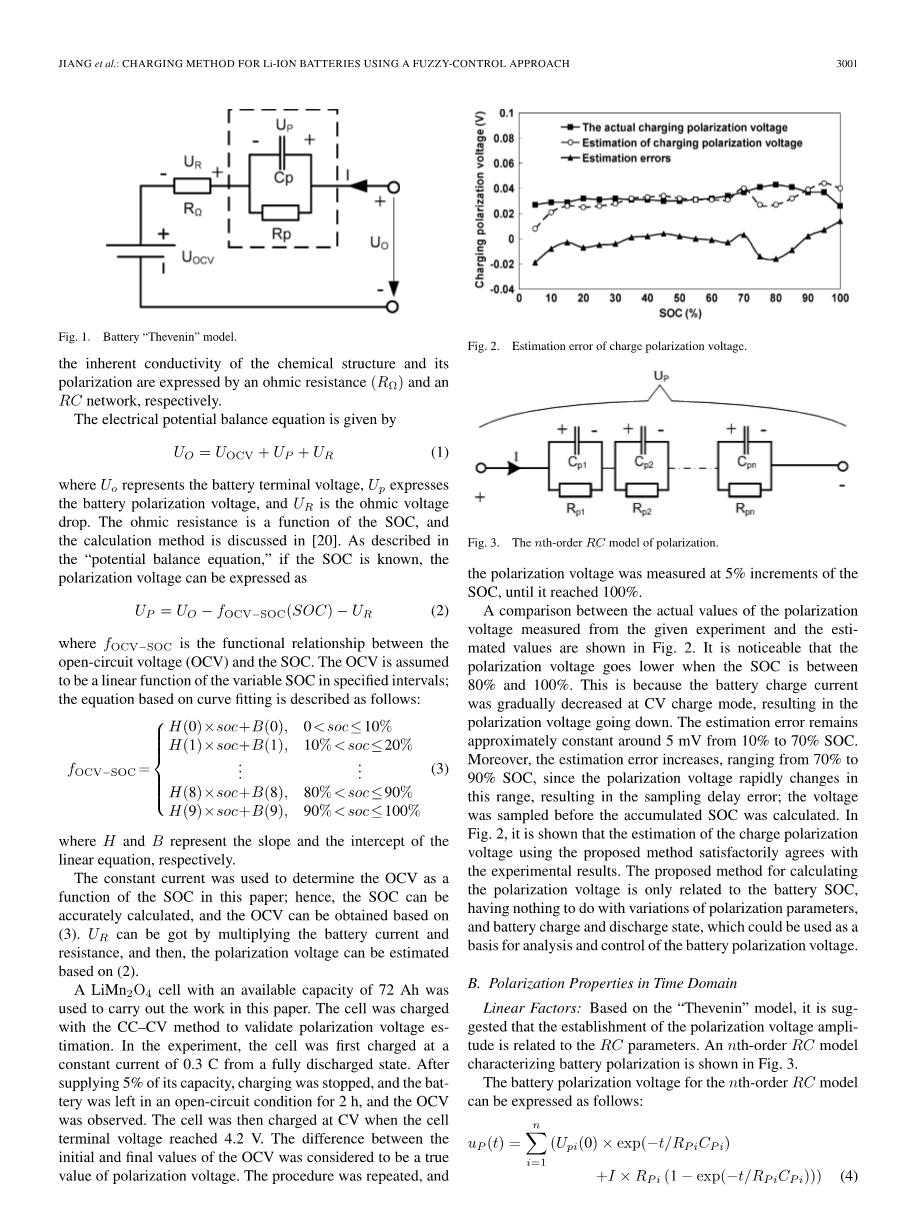
图2:极化充电电压的估计误差
图3:极化的n阶RC模型
所给实验中确认的极化电压的真实值之间的比较和估计值如图2所示,很明显可以看出,当SOC在80%到100%之间时极化电压变低了,这是因为当电池以恒压方式充电时,电池充电电流逐渐减少,从而导致极化电压下降。估计误差保持在大约5mv从10%到70%SOC。此外,估算误差从70%SOC到90%SOC开始逐渐增加,在这个范围内,极化电压也在急剧的变化,从而导致采样延迟误差;电压在累计SOC计算前被采样。正如图2所示,这种充电极化电压的估计值所使用的该种方法和试验结果非常符合。这种计算极化电压的方法只和电池SOC有关,和极化参数的变化和电池的充放电状态无关,而这可以作为电池极化电压的分析和控制的基础。
B.时间领域的极化功能
线性因素:建立在戴维宁模型的基础上,极化电压振幅的建立和RC参数有关。图3所示为描述电池极化的n阶RC模型。
n阶RC模型的电池极化电压表达式如下所示:
表1:不同电流下的充电极化电压(SOC=0)
代表n阶RC模型的初始极化电压,代表电池的充电电流,这表明在经过一段时间的充电后,k阶RC模型达到了饱和状态。等式(4)可以重新修改为
为n阶RC模型的总的初始极化电压。饱和状态的时间表达式如下:
代表充电总时间,在n阶RC模型中,高频集总元件先于低频集总元件到达饱和状态,等式(5)可以重新修改为
规定
A1,...AN 代表极化电压的线性影响因素,它描述了在相同电流下RC电路不同顺序下的电池极化现象。
时间参数T的极化电压由两个部分组成:饱和部分和非饱和部分,饱和状态下的极化由描述,非饱和状态下的极化由和描述。
非线性因素:为了研究电池极化状态下充电电流的效果,样本电池从完全空载状态到最大电压状态以24A到72A的恒定电流充电。极化电压的值在第900秒时用评估的方法得到。从表1的数据可以清楚的看出极化电压很明显的受到充电电流的影响。极化电压的振幅和充电电流之间是单调递增函数关系。如果我们假设电池的极化阻抗完全受RC模型的参数影响,则极化电压就被认为和充电电流之间有线性关系,如果
表2:不同初始SOC下的充电极化电压
,则。然而,表1中的数据认为不等于。这说明极化阻抗和充电电流之间不是线性关系。考虑到非线性性,电流畸变系数被添加到“A multiphase battery charger with pulse charging scheme,”中。电流畸变系数在电流达到2/3C时的情况在文章中已经描述出来了,同时在电流I时也体现出来了。的功能和充电电流可以通过曲线拟合获得,归一化系数如表1所示。实验结果表明单元电流引起的畸变系数在低电流时是很小的。它随着充电电流的变大而变大。
表2描述了不同的初始SOC的特殊的时间节点下样本电池的初始极化水平,在这个试验中,样本电池先以0.3C(24A)的电流充电直到达到额定容量的10%,然后保持开路状态半个小时以消除电池的极化。然后再以相同的电流充电额定容量的10%。在整个过程中,极化电压在T=900s时得出,然后如表2所示,重复上述过程来获得剩下的数据点。如表二所证明的,相同电流情况下,极化电压随着初始SOC的变化而变化。这可以用添加SOC的畸变系数来解释。当SOC为10%时SOC的畸变系数在1中已经描述过了,KSOC=(Up-soc)/(UP|soc=10%)
因此,如表2所示KSOC和SOC之间的关系可以通过曲线拟合和归一化系数KSOC获得。为了研究充电极化电压的初始电池极化状态的效果,进行了一系列的实验,电池先在0-, 0.5-,1-, 2-,和5-h状态下在额定时间内用0.3C的电流充电,所有的实验都在初始SOC为0%的条件下进行。充电极化电压在T=900s时的结果都被提取出来。数据如表3所示,
通过表3可以看出在电流给定的条件下极化电压随着放电后放置时间的缩短而减小。在之前持续时间从0到1小时所产生的极化电压是明显不同的,而在1小时之后所产生的极化电压几乎是相同的。这就是说:
表3:不同持续时间后的极化充电电压
图4:从第1次到第100次循环电池充电极化电压的特性(SOC=0%,充电电流=24A)
极化现象在电池保持开路状态一个小时后基本就消失了。考虑到电池充电极化现象的初始极化状态的影响,电池初始极化状态的影响因子BPO-,所以需要被添加进去。充电开始前的持续时间反映了电池的初始极化状态;BPO-和电池操作条件的相对对应关系如下:
根据极化电压的滞后效应,先前电池的消除两极分化状态随着不同的初始持续时间短变化而变化,这也反映了极化电压的振幅,这也展示了电流极化状态的一个叠加效应。
电池不同循环数的充电极化电压如图4所示。在图4中,电池的充电极化电压随着充电-放电循环的增加而增加。这是因为充电转移了阻抗同时电解液分解、电极腐蚀、活跃的活性物质结构变化和其他电池的退化导致了大量转移的阻抗的增加。因此,电池寿命计算的需要把极化电压的计算考虑进去。如图4所示,增量在特定的寿命状态下基本保持恒定。我们假设BSOH=UP-aged-UP-new,UP-aged特定寿命下的极化电压,UP-new代表新电池的极化电压。非线性功能BSOH=f(Ncycle number)可以由建立在实验结果上的曲线拟合获得。
正如先前所讨论的,充电极化不仅和RC参数有关,也与电流、初始SOC、初始持续时间和电池的寿命有关。考虑到所有的影响因子,时间方面的充电极化电压的配方在(9)中已经列出来了。因此
因K1代表电流系数,KSOC是初始SOC的状态参数,BSOH代表电池的寿命系数,BPO-是初始极化状态参数。
C.SOC领域的极化功能
为了分析SOC领域的极化功能,SOC的及话题度可以假设为:
通过给定的论述中可以知道,在时间领域,不同电流、初始SOC、持续时间或者循环寿命所产生的极化电压是不同的,同时极化电压变稳定的时间也是不同的。为了调查电池随着SOC变化的充电极化特性,建立在表1-3和图4的实验数据的基础上,SOC的极化电压变量被提取了出来。充电电流、初始SOC、初始极化状态和SOC的电池极化电压变量的效果也在图5(a)-(d)中相对的反映出来了。
正如图5(a)所示,初始充电极化电压变量随着电流的变化而变化,很明显可以看出在不同充电电流的条件下,充电极化电压变量的拐点所产生的SOC的增量几乎是相同的。这幅图也说明了如果其他状态例如初始SOC、初始极化状态和寿命的等级相同的情况下,SOC的极化电压变量的拐点和电池充电电流是相互独立的。在图5(b)-(d)中,不同初始SOC、不同的初始极化状态和不同寿命等级下SOC的极化电压变量的拐点始终如一,同时当电池SOC超过5%时,极化电压的变量变成了一个很小的稳态值。另外如图5(c)所示,完全放电后电池的放置时间越短,SOC的充电极化电压变量的初始值越小。如图5(d)所示,SOC的充电极化电压变量的振幅随着电池降解而增加;然而拐点并没有被改变。总结:SOC曲线的充电极化电压的梯度有一个拐点,这和电流、初始SOC、初始极化状态和电池老化程度之间是相对独立的。极化电压梯度是相对稳定的,而且在拐点出现以后保持了一个很小的值,这也为充电极化电压和SOC估算提供了一个基础。
图5:SOC的充电极化电压梯度的特性(a)不同电流下SOC函数的电池极化电压梯度(b)不同初始SOC下SOC函数的
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[149939],资料为PDF文档或Word文档,PDF文档可免费转换为Word


