
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
市场不稳定性预测:成交量与波动性之间的新动态
经济物理学和计量经济学一致认为,在一个时间序列中,成交量和波动率之间存在相关性。利用经验数据及其分布,我们进一步研究了这种相关性,并发现了新的方法波动性和成交量相互作用,特别是当两者的水平都很高时。我们发现成交量条件波动率与指数截止的幂律函数很好地拟合。我们发现成交量条件波动率分布与成交量成比例,并将这些分布压缩为单个曲线。我们利用容积波动率散点图的特征发现对数量和一个我们定义为局部最大波动率(LMV)的量,它表示最大的在给定交易量范围内观察到的波动性。这一发现支持我们的实证分析该成交量是一个很好的预测同一天和近期波动性最大值的指标时期。我们还使用包含波动率和成交量的联合条件概率来证明两种方法都可以比单独使用两种方法更好地预测次日的最大波动率。
绪论
投资者普遍知道交易量与价格变化密切相关[1,2],长期以来,金融市场的价格量关系一直是经济学家的热门研究课题。尽管研究一致认为,绝对价格变化(波动率)与交易量之间存在相关性[3],但许多研究表明这种相关性很弱[4],并且他们对时滞相关性的分析产生了各种矛盾的结果[5–12]。体积和挥发性之间关系的微妙之处仍然不清楚 [13] ,分歧仍然存在。例如,Brailsford等。报告隔夜回报与交易量之间存在显着的互相关性[14]。布鲁克斯(Brooks)指出,将滞后量包括在内可能会导致预测性能的适度提高[15],而克拉克则显示出体积和波动率之间几乎呈抛物线的函数关系[16],而克拉克开发的流行模型认为波动率可以建模为次级随机过程,其中,在影响交易时间的范围内,交易量占观察到的波动性集群和瘦态(即尾巴很重)的大部分。另一方面,一些研究报告称,名义上,交易量仅在预测波动率方面有用。Koulakiotis等。报告了波动率和交易量之间的负相关关系[17]。Lam-oureux和Lastrapes表明,当方差方程中包含体积时,ARCH效应趋于消失(即,失去了波动性持续性)[6]。Sharma等。甚至暗示,在没有交易量作为混合变量的情况下,GARCH模型可以最好地描述纽约证券交易所的价格收益[18]。最近,Gillemot等。结果表明,Clark开发的次标准随机过程最多只占观察到的波动性聚集和瘦峰度的一小部分[19]。
为了揭示数量与波动率之间的潜在关系,我们着重研究这两个数量的最基本特征,首先检查每个数量的概率密度函数(pdf)以及数据集中波动率的体积条件pdf 。基于这些基本分析,我们表明,当对波动率单位进行适当缩放时,体积条件波动率的pdf实际上在体积变化下是不变的,这与Yamasaki等人所做的类似工作密切相关,后者报告了普遍的缩放比例波动率返回区间的函数[25]。然后,我们提出了一个新的概率密度函数,该函数将波动率和交易量的发生联系起来。我们将进一步研究在某 些交易量制度中波动率分布的最高部分,并提出一个我们称为“局部最大波动率”(LMV)的量,我们将其显示为与给定日的交易量以及交易日的交易量密切相关以前。
数据与方法
我们使用1990年4月至2007年6月这17年时间段的每日价格,分析了包含道琼斯工业平均指数的30只股票,共计130,410个数据点。由于与世界金融危机有关的交易时间序列可能存在高度不稳定的可能性,因此我们避免使用2007年6月以后的数据,尽管进一步的分析表明,包括2007年后的数据,我们的结果不会改变。对于30只股票中的每只,我们计算价格的每日对数变化(通常称为收益):
(1)
以及每日标准化对数交易量,根据交易量计算得出:
(2)
对于给定的股票i,其中表示的最小二乘线性拟合[20],这消除了整个17年期间的全球趋势。对于每种不同的股票,我们根据原始收益和原始对数来定义归一化波动率
(3)
和归一化对数体积。
(4)
其中表示研究期间的平均时间。这里和是和的标准偏差。注意:波动率是用绝对值表示的,而对数交易量可以是正数,也可以是负数。在本文中,体积表示归一化对数体积,波动率表示归一化波动率。
分析
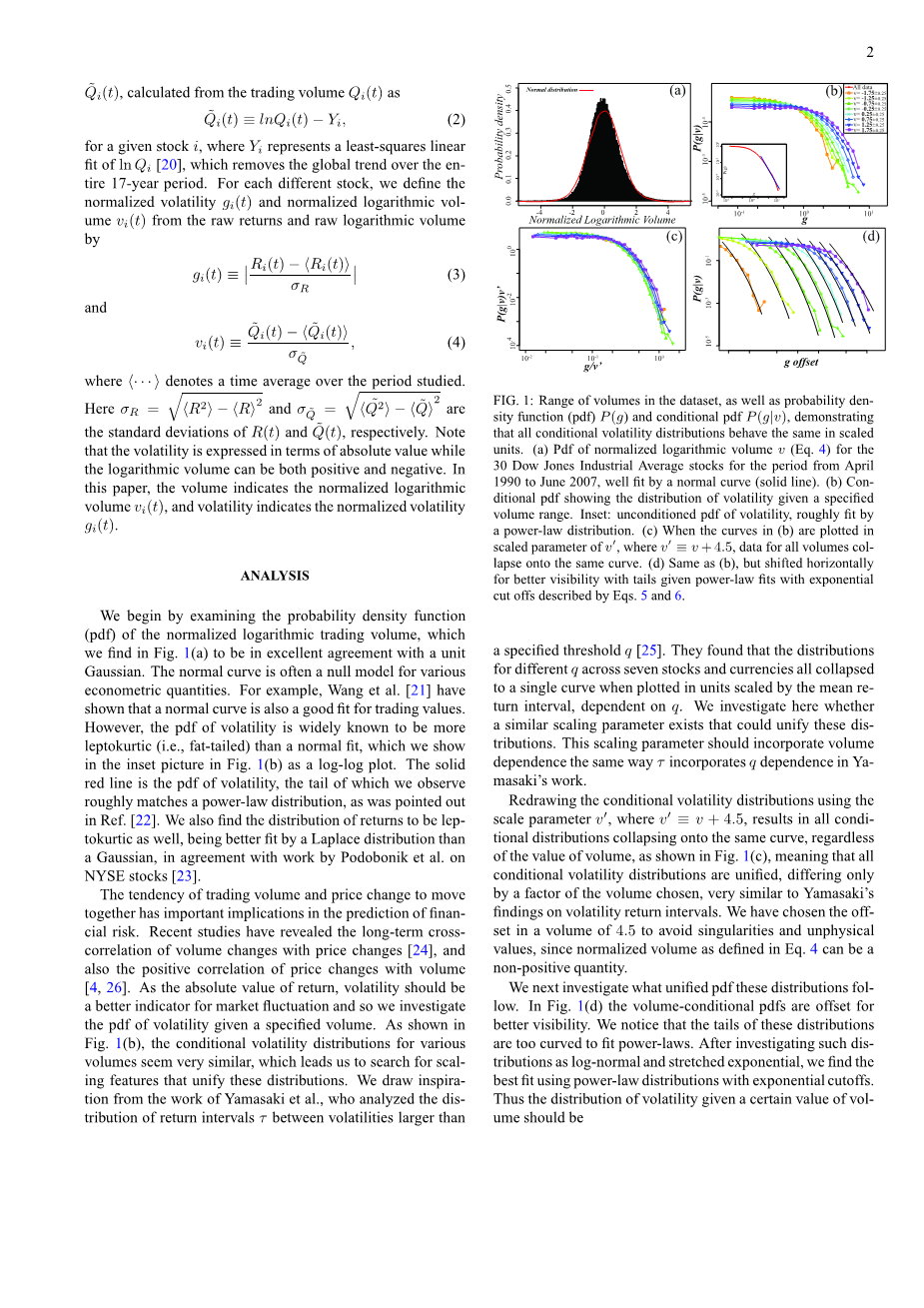
我们首先检查归一化对数交易量的概率密度函数(pdf),我们在图1(a)中发现其与单位高斯极吻合。对于各种计量经济量,法线通常是无效模型。例如,Wang等。[21]已经表明,正态曲线也很适合交易价值。然而,众所周知,波动率pdf比正常拟合更瘦弱(即,肥尾),我们在图1(b)的插图中以对数-对数图形式显示。红色实线是波动率的pdf,我们观察到的尾部与幂律分布大致匹配,如Ref。1中所述。[22]。与Podobonik等人的 工作一致,我们还发现收益的分布也很瘦弱,与Laplace分布相比,高斯分布更适合Laplace分布。纽约证交所股票[23]。
交易量和价格变化共同趋向的趋势对财务风险的预测具有重要意义。最近的研究揭示了价格变化与价格变化的长期相互关系[24],以及价格变化与数量的正相关[4,26]。作为收益的绝对值,波动率应该是市场波动的更好指标,因此我们调查在给定数量的情况下的波动率pdf。如图1(b)所示,各种体积的条件波动率分布看起来非常相似,这使我们寻找统一这些分布的缩放特征。我们从Yamasaki等人的工作中汲取了灵感,他们分析了大于30%的波动率之间的收益区间tau;的分布:sity函数(pdf)和条件pdf ,表明所有条件波动率分布在换算单位上的表现都相同。(a)1990年4月至2007年6月期间30只道琼斯工业平均指数股票的归一化对数交易量v(方程式4)的Pdf很好地拟合了一条正态曲线(实线)。(b)有条件的pdf,显示指定体积范围内的波动性分布。插图:无条件的pdf波动率,大致适合幂律分布。(c)当(b)中的曲线以v′的比例参数绘制,其中时,所有体积的数据都折叠到同一条曲线上。(d)与(b)相同,但水平移动以提高尾部的可见度,前提是幂律与方程式5和6所描述的指数截止相吻合。指定的阈值q [25]。他们发现,当以按平均回报间隔(取决于q)定标的单位绘制时,七种股票和货币中不同q的分布全部折叠为一条曲线。我们在这里调查是否存在可以统一这些分布的类似缩放参数。此缩放参数应包含音量依赖性,就像tau;在Yas工作中包含q依赖性一样。
使用比例参数v′重绘条件波动率分布,其中,导致所有条件分布都折叠到同一条曲线上,而不管体积值如何,如图1(c)所示),表示所有有条件的波动率分布是统一的,仅相差一个选定的量,与山崎对波动率回报区间的发现非常相似。我们选择了 4.5的偏移量,以避免奇异和非物理值,因为等式中定义了标准化体积4可以是非正数。
图1:数据集中的体积范围以及概率密度
接下来,我们将研究这些分布如何统一pdf。在图1(d)中,对体积条件pdf进行了偏移以提高可见性。我们注意到这些分布的尾巴太弯曲而无法拟合幂律。在研究了对数正态分布和拉伸指数分布之后,我们发现使用幂律分布和指数截止值的最佳拟合。因此,在给定一定数量的交易量的情况下,波动率的分布应为:
图2:拟合的联合波动率和交易量。
使用alpha;,beta;,a,b的拟合值,我们显示了等式的概率密度函数的等高线图。6拟合图1(b)中的数据,我们表明,降低g(波动率)或增加v(体积)会导致概率密度单调增加。较高的波动率在其范围内的波动远比较低的波动率大,这导致有可能根据交易量预测较高的波动率。
∽(5)
但是,如图1(c)所示,上述pdf可以按v′()进行缩放,这导致我们将体积添加为条件波动率分布函数的变量。因此我们假设和,使等式5变成:
∽(6)
使用图1(b)所示数据的最大似然估计,我们发现alpha;=0.4,beta;= -1.23,a-2.5和b =3。我们使用这些参数与等式绘制等高线图。图2中的图6示出,g(挥发性)和v(体积)在给定一定的概率密度值的情况下同时增加。具体来说,我们注意到虽然在整个交易量范围内均会出 现低波动性,但较高的波动性仅在较大的交易量中才会有很强的趋势,这意味着从交易量中可以预测出高波动性,尽管低波动性无法预测。
结果,我们将分析限制在包含最大波动率的日子里,这是适当的,因为高波动率的日子是交易员和市场研究人员最感兴趣的日子。为此,我们引入数量“局部最大 波动率”(LMV),由于它与给定日的交易量和前几天的交易量密切相关,因此可以做出预测性声明。
图3
图3:虽然波动率与交易量并不高度相关,但是LMV与今天的交易量和昨天的交易量都高度相关(显示的LMV线性拟合)。在我们研究的整个过程中,LMV天都在发生。显示的是波音公司(BA)的波动率与体积的散点图:(a)波动率g(t)与归一化对数体积v(t),(b)波动率g(t)与否--前一天的对数体积最小化,v(t minus; 1)。红色实心三角形表示g的每个bin中的最大值(从-3到3划出30个垃圾箱)。rho;0是对数体积与LMV(等式7)之间的相关系数,而rho;表示对数体积与波动率之间的相关系数。根据(c)并发交易量和(d)前一天交易量显示了LMV的波动性时间序列和LMV(红色三角形)。
我们通过将观察到的交易量范围划分为箱等来定义由glm表示的LMV参数。然后:
(7)
LMV是在给定交易量范围内观察到的最大波动率,即,同时发生了给定交易量的最波动日的波动率。尽管波动率和对数数量之间的相关性较弱,但我们发现,一般而言,LMV和对数数量高度相关。我们使用波音公司(BA)的示例在图3(a)中对此进行了演示。对于BA,我们观察到当日交易量与波动率之间的相关系数仅为0.5,而交易量与LMV之间的相关系数为0.93。我们使用图3中的波动率与体积的散点图进一步研究波动率与体积之间的相关性。在(a)波动率与当日交易量和(b)的散点图中,可以看到特征三角形。波动率与前一天的交易量。用于定义LMV的音量范围为如图1(a)所示,由定义的垃圾箱进行分类(30个垃圾箱从-3到3均匀划分)如方程式7中所定义。我们在每个给定仓中使用最高波动率。在这两种情况下,在视觉上用红色三角形显示与给定体积匹配的最大波动率,并在实线黑色中显示线性回归拟合计算出的相关性。由于LMV中使用的波动率可能起源于狭窄的,异常波动的时间窗口(例如一周),因此给出了虚假的结果,因此我们研究了使用高波动率日的时间。图3(c)和3(d)表明,这些高波动日的确确实发生在整个所考虑的时间段,以确保LMV的普遍代表性。
图4
图4:波动率和交易量(红色方块)之间没有很强的相关性,尽管这种影响会随着时间的流逝而迅速消失。在整个时滞范围内,LMV与音量(黑圈)的相关性更强。显示的是30种道琼斯工业平均指数的平均相关系数与时滞的关系。误差线表示plusmn;标准偏差。注意,时滞的平均相关系数=0天,1天与图4中的非常相似,图4仅描述了波音公司(BA)的结果。
现在,我们将图3所示的当日和一日偏移量的分析推广到最多16天的可变时间偏移量。我们的结果如图4所示。在图中,我们显示了30只道琼斯工业平均指数股票相对于时滞的平均相关系数。该图显示,在几乎所有非零时滞范围内,体积与波动率之间的相关性迅速降至零,而体积与LMV之间的相关性滞后一天保持显着值(asymp;0.4),即使滞后四天也保持显着(asymp;0.2),表明预测最大天数的巨大潜力波动性,从而带来最大风险,这在金融危机期间对保护投资极为重要[27]。
可能的波动率与当日交易量紧密相关的事实是很直观的,因为价格可以变化的程度是在一天中发生的交易量的函数。交易量与未来波动率之间的联系更加有趣。由于众所周知,波动性在不久的将来会与其自身的价值相关联,因此这一结果似乎微不足道。稍后我们提供证据(参见图5),表明我们的发现超出了这一显而易见的结果,即包含体积确实确实在预测方案中添加了非冗余信息。此外,正如Gillemot等人所表明的那样。此外,Gillemot等人也证明了这一点:波动性向集群的趋势并不是由于平均交易时间减少而产生的简单的成交量效应[19]。
图5(a)和(b)示出了和的条件分布。在此,表示包含最高1%或最低1%波动率的子集。图5(a)显示了今天的交易量,给定明天的波动率,而图5(b)显示了今天的交易率,给定明天的波动率。在没有记忆效应的情况下,5(a)和5(b)在最高和最低波动率情况下都是完全平坦的分布。相反,我们清楚地看到了在最高情况下的记忆效应。20%的交易量占最高(前1%)波动率前几天的大约40%。这种影响在五分位数中是单调的,而代表性不足的最极端例子是,最低20%的交易量约占最高波动率的10%。对于最低的1%波动率,我们认为没有这种影响。低波动之前的天数分布在统计上与整个交易量的均匀分布相同。低波动率日在成交量上没有统计上不同的分布,这与图2所示的早期观察一致,即低波动率在成交量上具有广泛的范围,因此无法从成交量上预测。当考虑到第二天的波动率时,我们会观察到类似的结果,因为我们知道第二天的波动,率会特别高或特别低。同样,在最高波动率的五分位数中,高波动率之前的天数过高,但是在最低波动率的前,几天中,波动率在五分位数中基本上是平坦的。
lt;
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[238483],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


