本科毕业设计(论文)
外文翻译
使用ARIMA模型预测股票价格
作者:Adebiyi A. Ariyo ; Adewumi O. Adewumi ; Charles K. Ayo
国籍:南非,南非,尼日利亚
出处:2014年UKSim-AMS第16届计算机建模和仿真国际会议
中文译文:
摘要:股票价格预测是金融学和经济学的一个重要课题,近年来引起了研究者们对建立更好的预测模型的兴趣。求和自回归移动平均(ARIMA)模型在时间序列预测中得到了广泛的应用。本文介绍了利用ARIMA模型建立股票价格预测模型的广泛过程。利用纽约证券交易所(NYSE)和尼日利亚证券交易所(NSE)公布的股票数据,建立了股票价格预测模型。结果表明,ARIMA模型具有较强的短期预测潜力,可与现有的股票价格预测技术相媲美。
关键词:ARIMA模型;股票价格预测;股票市场;短期预测.
一.导言
预测将继续是一个有趣的研究领域,使该领域的研究人员总是希望改进现有的预测模型。其原因是,机构和个人有权作出投资决定,并有能力规划和制定关于其日常和未来困境的有效战略。由于股票市场的复杂性[1,2,3],股票价格预测被认为是财务预测中最难完成的任务之一。许多投资者的愿望是掌握任何可以保证容易获利和尽量减少股票市场投资风险的预测方法。这仍然是促使研究人员进化和开发新的预测模型的一个因素[4]。
在过去的几年里,人们发展了多种股票价格预测模型和技术。其中人工神经网络(ANNs)模型由于具有从数据中学习模式和从未知数据中推断解的能力而受到人们的青睐。采用ANNs模型进行股票价格预测的相关工作较少[5,6,7]。近年来,混合方法也被用于改进股票价格预测模型,利用每一个[2]的独特优势。ANNs是从人工智能的角度。
ARIMA模型是从统计模型的角度。一般来说,文献中有报道说,可以从两个角度进行预测:统计和人工智能技术[2]。众所周知,ARIMA模型在金融时间序列预测中具有强平稳性和有效性,特别是在短期预测方面,甚至比最流行的ANS技术([8,9,10])都要好。它在经济和金融领域得到了广泛的应用。其他统计模型有回归法、指数平滑法、广义自回归条件异方差(GARCH)。使用ARIMA模型进行预测的相关工作很少[11、12、13、14、15、16]。
本文介绍了建立ARIMA短期股价预测模型的广泛过程。从实际数据中得到的结果表明,ARIMA模型在为投资者提供短期预测方面具有潜在的优势,可以帮助投资者进行投资决策。
论文的其余部分组织如下。第二节简要介绍了ARIMA模型。第三节介绍了实验方法,而第四节则讨论了所获得的实验结果。本文的结论在第5节。
- ARIMA模型
Box和Jenkins在1970年引入了ARIMA模型。它也被称为Box-Jenkins方法,由一用于识别、估计和诊断具有时间序列数据的ARIMA模型的一系列活动组成。该模型是金融预测中最突出的方法[1,12,9]。ARIMA模型显示了生成短期预测的有效能力。在短期预测方面,它明显优于复杂结构模型[17]。在ARIMA模型中,变量的未来值是过去值和过去误差的线性组合,表示如下:
- 其中,是真实值,是t处的随机误差,和是系数,p和q是常被称为自回归和移动平均的整数。
建立ARIMA预测模型的步骤包括模型识别、参数估计和诊断检验[18]。
三、方法论
本文详细介绍了建立ARIMA股票价格预测模型的方法。用于实现的工具是Eviews software version 5。本研究中使用的股票数据是从两国股票交易所获得的历史日股价。数据由四个要素组成,即:开盘价、低价、高价、收盘价。在本研究中,选择收盘价来表示将要预测的指数的价格。选择收盘价是因为它反映了指数在一个交易日的所有活动。
为了确定多个实验中的最佳ARIMA模型,本研究对每种股票指数采用以下准则。
·BIC相对较小(Bayesian或Schwarz信息准则)
·相对较小的回归标准误差(回归标准误差)
·调整后的值相对较高
· Q-统计量和相关图表明,残差的自相关函数(ACFs)和部分自相关函数(PACFs)不存在显著的模式,这意味着所选模型的残差为白噪声。
下面的小节描述了ARIMA模型的发展过程。
- ARIMA(p,d,q)诺基亚股票指数模型
本研究使用的诺基亚股票数据涵盖1995年4月25日至2011年2月25日这段时间,共有3990个观测值。图1描述了该序列的原始模式,从而对时间序列是否平稳有了大致了解。从下图中可以看出,时间序列有随机游动模式。
图1:诺基亚股票收盘价格指数的图形表示
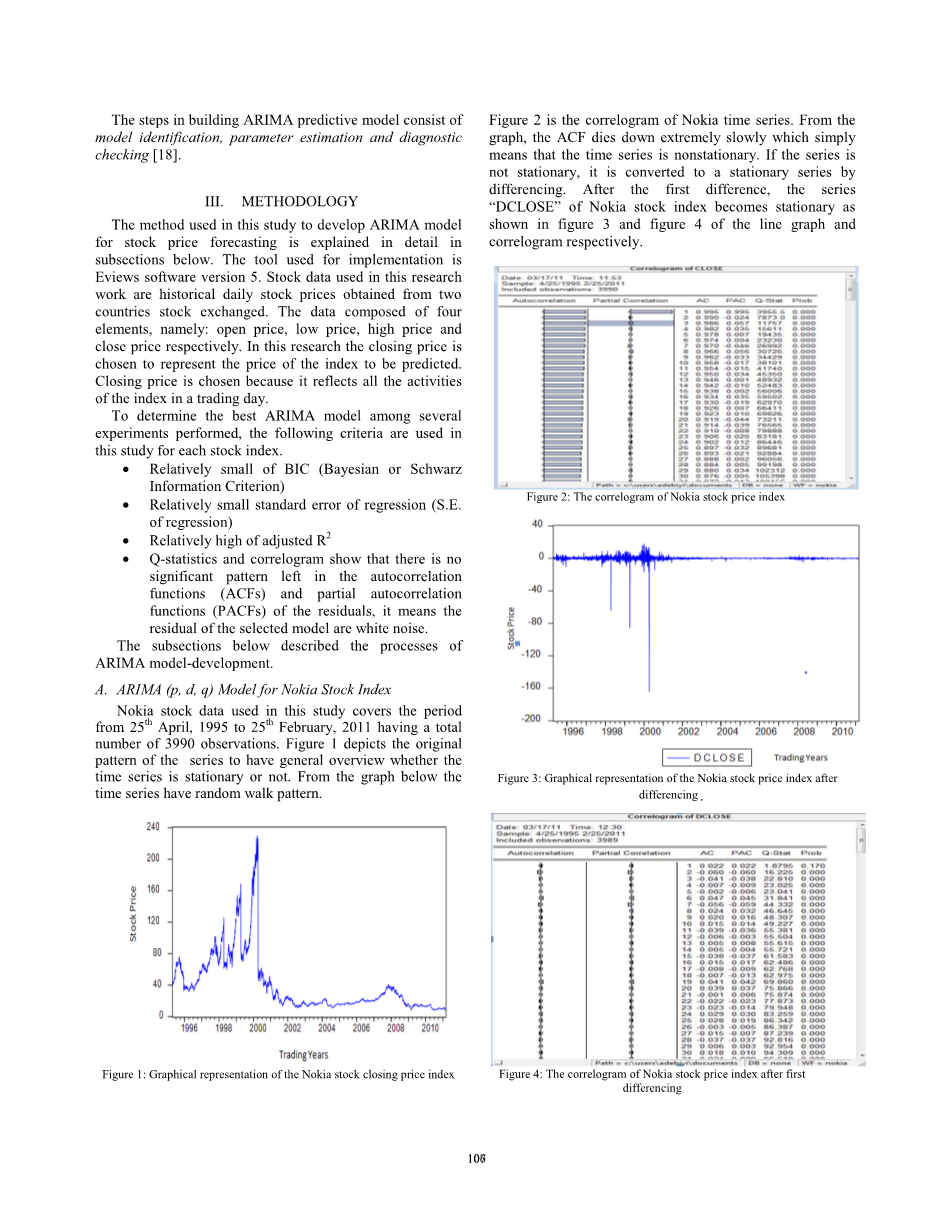
图2是诺基亚时间序列的相关图。从图上看,ACF的衰减非常缓慢,这就意味着时间序列是非平稳的。如果序列非平稳,则通过差分转换为平稳序列。经过第一次之后,诺基亚股票指数的系列“DCLOSE”变得平稳,如图3和图4所示线图和相关图。
图2:诺基亚股价指数的相关图
图3:差分后诺基亚股价指数的图形表示
图4:第一次差分后诺基亚股价指数的相关图
在图5中,模型检验使用诺基亚股票指数“DCLOSE”上的Augmented Dickey Fuller (ADF)单位根检验完成的。结果表明,该序列经过一阶差分后趋于平稳。
图5:诺基亚股票指数DCLOSE的ADF单位根检验
表1给出了几种ARIMA模型的自回归(p)和移动平均(q)的不同参数。ARIMA(2,1,0)被认为是诺基亚股票指数的最佳选择,如图6所示。模型将最小的Bayesian或Schwarz信息准则重新调整为5.3927,相对最小的回归标准误差为3.5808,如图6所示。
图6:ARIMA(2,1,0)使用诺基亚索引的DCLOSE的估算输出
图7是该系列的剩余部分。如果模型良好,则模型的残差(实际值与预测值之差)是一系列随机误差。由于ACFs和PACFs没有显著的峰值,这意味着所选ARIMA模型的残差是白噪声,在时间序列中没有其他显著模式。因此,没有必要进一步考虑任何AR(p)和MA(q)。
图7:诺基亚股票指数残差的相关图
在预测形式中,所选择的最佳模型可表示如下:
(2)
其中, (即序列的实际值与预测值之差)
表I:不同ARIMA参数的诺基亚股票指数的统计结果
粗体的一行表示几个参数中最好的ARIMA模型。
- Zenith银行指数的ARIMA(p,d,q)模型
本研究使用的Zenith银行股票数据涵盖2006年1月3日至2011年2月25日这段时间,共观测1296次。图8是该系列的原始模式。从图上看,该指数从2006年开始向上移动,从2008年起下降了107,108,可能是因为世界金融c的缘故。当时的危机。图8是该序列的原始状态。从图上可以看出,该指数自2006年起呈上升趋势,2008年可能由于世界金融危机,该指数自2008年起呈下降趋势。
图8:Zenith银行股票指数收盘价的图形表示
图9是Zenith银行股票指数时间序列的相关图。从相关图上看,ACF的衰减非常慢,这就意味着时间序列是非平稳的。如果序列不是平稳的,则需要通过差分将其转换为平稳序列。在第一次差分之后,Zenith银行股票指数的“DCLOSE”序列变得平稳,如图10和图11所示,该序列的线图和相关图经过在第一次差分后变得平稳。
图9:Zenith银行股价指数的相关图
图10:Zenith银行股票指数一次差分后的图形表示
图11:Zenith银行股价指数第一次差分后的相关图。
图12是对该序列的“DCLOSE”的ADF单位根检验,它也表明序列经过第一次差异变得平稳。
图12:Zenith银行股票指数DCLOSE的ADF单位根检验
表2给出了ARIMA模型的自回归(p)和移动平均(q)的不同参数,从而得到最佳拟合模型。ARIMA(1,0,1)是相对最好的模型,如图13所示。该模型返回最小的Bayesian或Schwarz信息准则为2.3736和回归相对最小的标准误差为0.7872,如图13所示。
图13:ARIMA(1,0,1)用Zenith银行指数的DCLOSE估计输出
图14是序列残余的相关图。从图中可以明显看出,ACFs和PACFs没有明显的峰值。这意味着所选ARIMA模型的残差是白噪声。在时间序列中没有其他重要形式,也没有必要进一步考虑另一个AR(p)和MA(q)。
图14:Zenith银行股票指数残差图
在预测形式上,所选择的最佳模型可表示如下:
(3)
其中, (即序列的实际值与预测值之差)
表II:不同ARIMA参数的Zenith股票指数的统计结果
粗体的一行表示几个参数中最好的ARIMA模型。
四、结果和讨论
以下小节讨论了每种股票指数的实验结果。
- ARIMA模型在诺基亚股价预测中的应用
表3是ARIMA(2,1,0)的预测值,被认为是诺基亚股票指数的最佳模型。
图15给出了预测价格相对于实际股价的水平准确性的图形说明,以查看所选ARIMA模型的性能。从图上看,很明显性能是令人满意的。
表Ⅲ:诺基亚股票指数ARIMA(2,1,0)实证结果样本
图15:诺基亚股票指数实际股价与预测值的关系图
- ARIMA模型对Zenith银行股价预测结果
在本例中,使用Eviews软件中对自回归(p)和移动平均(q)参数进行了多次调整后,选取了ARIMA(1,0,1)作为Zenith银行股票指数的最佳模型。表4为所选模型的预测值,图16是预测价格与实际股价的关系图,以说明准确性的相关性。从图中可以看出,所选择的ARIMA模型的性能令人印象深刻,因为有一些与实际值和预测值密切相关的实例。
表Ⅳ:Zenith银行指数ARIMA(1,0,1)经验结果样本
图16:Zenith银行股票指数实际股价与预测值的关系图
- 结论
本文介绍了建立股票价格预测ARIMA模型的广泛过程。利用最优ARIMA模型得到的实验结果证明了ARIMA模型在短期内预测股票价格的潜力。这可以引导股票市场的投资者做出有利可图的投资决策。结果表明,ARIMA模型的结果可以在短期预测方面与新兴的预测技术进行合理的竞争。
参考文献:
[1] P. Pai and C. Lin, “A hybrid ARIMA and support vector machines
model in stock price prediction”, Omega vol.33 pp. 497-505, 2005
[2] J.J. Wang, J.Z. Wang, Z.G. Zhang and S.P. Guo, “Stock index
forecasting based on a hybrid model”, Omega vol.40 pp.758-766,
2012.
[3] L.Y. Wei, “A hybrid model based on ANFIS and adaptive
expectation genetic algorithm to forecast TAIEX”, Economic
Modelling vol. 33 pp. 893-899, 2013.
[4] G.S. Atsalakis, E.M Dimitrakakis. and C.D. Zopounidis, “Elliot
Wave Theory and neuro-fuzzy systems, stock market prediction: The
WASP system”, Expert Systems with Applications, vol. 38, pp.9196–
9206, 2011.
[5] S. K.Mitra, “Optimal Combination of Trading Rules Using Neural
Networks”, International Business Research, vol. 2, no. 1, pp. 86-99,
2009.
[6] G.S. Atsalakis and P.V. Kimon, “Forecasting stock market short-term
trends using a n
剩余内容已隐藏,支付完成后下载完整资料

英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[272332],资料为PDF文档或Word文档,PDF文档可免费转换为Word


