
英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
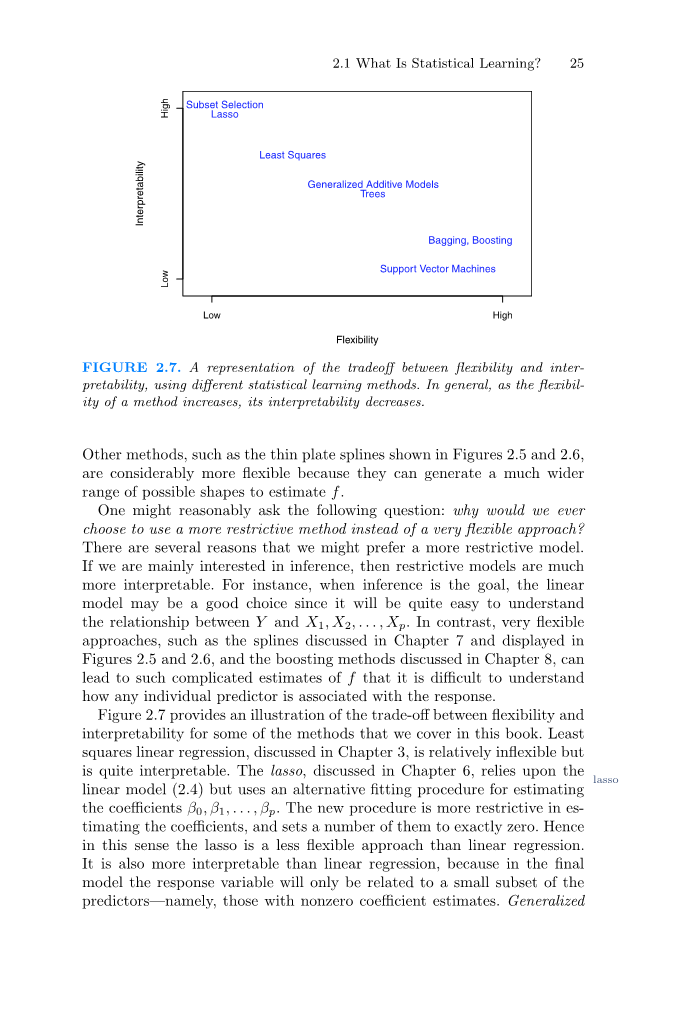
图2.7 在灵活性和可解释性之间权衡的一种表示,使用不同的统计学习方法。通常,随着方法灵活性的增加,其可解释性会降低。
另外,如图2.5和图2.6中所示的薄板样条,则灵活的多,因为它们可以生成更大范围的可能形状来估计f。
人们可能会合理的问这样一个问题:为什么我们会选择使用一种限制性更强的方法而不是一种非常灵活的方法呢?我们可能更喜欢限制性强的模型有几个原因。如果我们主要对推理感兴趣,那么限制性模型就更容易解释。例如,当推理是目标时,线性模型可能是一个很好的选择,因为它很容易理解Y和X1,X2,...,Xp 之间的关系。相反,非常灵活的方法,例如第七章中讨论的样条曲线和图2.5和图2.6中显示的样条曲线,以及第八章中讨论的增强方法,会导致对f的估计非常复杂,以至于很难理解单个预测器如何与响应相关联。
图2.7展示了我们在本书中介绍的方法的灵活性和可解释性之间的平衡。最小二乘线性回归,在第三章中讨论,是相对不灵活的,但很容易解释。第六章讨论的套索依赖于套索模型(2.4),但使用了另一种拟合方法来估计系数 beta;0,beta;1,...,beta;p 。
新方法在估计系数方面有更多的限制,并设置了一些系数。因此,在这个意义上,套索是一种不如线性回归灵活的方法。它也比线性回归更容易解释,因为在最终的模型中,响应变量将只与预测器的一小部分相关——即那些系数估计为非零的预测器。在第七章中讨论的广义相加模型(GAMs)拓展了套索模型(2.4),以考虑某些非线性关系。因此,加性GAMs 比线性回归更灵活。它们在某种程度上也不如线性回归那么容易解释,因为每个预测器与响应之间的关系现在都是用曲线来建模的。最后,在第八章和第九章中讨论的非线性方法,如套索、升压和支持向量机用非线性核进行套袋是非常灵活但是很难解释的方法。
我们已经确定,当以推理为目标时,使用简单且相对不灵活的统计学习方法具有明显的优势。然而,在某些情况下,我们只对预测感兴趣,对预测模型的可解释性根本不感兴趣。例如,如果我们试图开发一种预测股票价格的算法,我们对该算法的唯一要求就是它的预测的准确性和可解释性,不是问题。在这种情况下,我们可能认为最好使用最灵活的模型。令人惊讶的是,情况并非总是如此,我们通常会使用不太灵活的方法获得更准确的预测。乍一看,这一现象似乎违反直觉,但它与高度灵活的方法可能会过度适应相关。我们在图2.6中看到了一个过拟合的例子。我们将在2.2节和全书中进一步讨论这个非常重要的概念。
2.1.4监督学习与非监督学习
大多数统计学习问题可分为两类:有监督的和无监督的。到目前为止,我们讨论的例子都属于有监督学习领域,对于每次观测的预测量测量xi, i = 1,...,n 。我们希望拟合一个将响应与预测因子联系起来的模型,以准确预测未来观测的响应,或更好的理解响应与预测因子(推断)之间的关系。许多经典的统计学习方法,如线性回归和逻辑回归(第四章),以及更现代的方法,如GAM, boosting, 和 support vec- regression tor machines,都是在监督学习领域中运行的。这本书绝大部分都是关于这个背景的。
相比之下,无监督学习描述的是更具有挑战性的情况,在这种情况下,每观察一次 i = 1,...,n, 我们观察到一个测量值x的向量,但没有相关的响应yi。线性回归模型是不可能拟合的,因为在这种情况下没有响应变量可以预测,我们在某种意义上是盲目的;这种情况被称为无监督,因为我们缺少一个可以监督我们分析的相应变量。什么是统计分析?
图2.8。包含三个组的聚类数据集。每个组使用不同颜色的符号表示。左:这三组被很好地分开了。在这种情况下,集群方法应该能够成功地识别这三个组。右图:这些组之间有一些重叠。现在集群任务更具挑战性。
可能吗?我们可以试图理解变量之间的关系或者观察值之间的关系。在这种情况下,我们可以使用一种统计学习工具,即聚类分析。聚类分析的目的是在x的基础上确定1hellip;hellip;,xn,观察结果是否属于相对不同的群体。例如,在市场细分研究中,我们可能会观察潜在客户的多个特征(变量),例如邮政编码、家庭收入和购物习惯。我们可能认为顾客分为不同的群体,比如大手大脚的和花钱不多的。如果每个客户的消费模式的信息是可用的,那么监督分析将是可能的。然而,这一信息是不可用的,也就是说,我们不知道是否每个潜在的客户都是一个大挥金如土的人。在这个设置中,我们可以尝试根据测量的变量对客户进行聚类,以便识别不同的潜在客户组。确定这些群体可能会引起兴趣,因为这些群体可能在某些利益属性方面有所不同,比如消费习惯。
图2.8简单地说明了集群问题。我们用两个变量X绘制了150个观测值1 和X2。每一项观察都对应于三个不同的组中的一个。为了便于说明,我们使用不同的颜色和符号绘制了每个组的成员。然而,在实践中,组成员身份是未知的,目标是确定每个观察对象所属的组。在图2.8的左边面板中,这是一项相对容易的任务,因为组是被很好地分离的。相反,右边的面板显示了一个更具挑战性的问题,其中有一些重叠。
两组之间。不能期望聚类方法将所有重叠点分配到正确的组(蓝色、绿色或橙色)。
在图2.8所示的示例中,只有两个变量,因此可以直观地查看观测结果的散点图,以便识别集群。然而,在实践中,我们经常遇到包含两个以上变量的数据集。在这种情况下,我们不能轻易地画出观测值。例如,如果我们的数据集中有p个变量,那么就可以生成p(p - 1)/2个不同的散点图,而目视检查根本不是识别集群的可行方法。因此,自动化集群方法非常重要。第10章讨论了聚类和其他非监督学习方法。
许多问题很自然地属于监督或非监督学习范式。然而,有时分析应该被认为是监督的还是非监督的问题就不那么明确了。假设我们有n个观测值。对于m个观测值,其中m lt; n,我们有预测量和响应量。对于剩余的n - m观测,我们有预测指标,但没有反应指标。如果可以相对便宜地测量预测器,但是收集相应的响应要昂贵得多,就可能出现这种情况。我们将这种设置称为半监督学习问题。在这种情况下,我们希望使用一种统计学习方法,这种方法可以包含m个观测值和n - m个观测值。虽然这是一个有趣的话题,但超出了本书的范围。
2.1.5 回归与分类问题
变量可以被描述为定量的或定性的(也称为范畴的)。定量变量具有数值。例子包括一个人的年龄、身高、收入、房子的价值和股票的价格。相反,定性变量在K个不同的类或类别中具有价值。定性变量的例子包括一个人的性别(男性或女性),购买的prod-uct品牌(品牌a、B或C),一个人是否拖欠债务(是或否),或癌症诊断(急性髓系白血病、急性淋巴细胞白血病或无白血病)。我们倾向于将具有定量响应的问题称为回归问题,而涉及定性响应的问题通常称为分类问题。然而,这种区别并不总是那么清晰。最小二乘线性回归(第3章)用于定量响应,而逻辑回归(第4章)通常用于定性(两类或二进制)响应。因此,它经常被用作分类方法。但是因为它估计类的概率,所以它可以被看作是一个回归方法。一些统计方法,如k近邻(第2章和第4章)和boost(第8章),可以用于定量或定性响应。
我们倾向于根据学生的反应是定性的还是定量的来选择统计学习方法;也就是说,我们可以在定量时使用线性遗憾,在定性时使用逻辑回归。然而,预测因子是定性的还是定量的通常不那么重要。本书中讨论的大多数统计学习方法都可以应用于任何预测变量类型,前提是在执行分析之前对任何定性预测因子进行适当编码。这将在第三章中讨论。
2.2 评估模型的准确性
本书的主要目的之一是向读者介绍广泛的统计学习方法,这些方法远远超出了标准的线性回归方法。为什么有必要引入这么多不同的统计学习方法,而不是单一的最佳方法?统计中没有免费的午餐:没有一种方法在所有可能的数据集上支配所有其他方法。对于一个特定的数据集,一种特定的方法可能工作得最好,而另一种方法可能对相似但不同的数据集工作得更好。因此,对于任何给定的数据集,确定哪种方法产生的结果最好是一项重要的任务。选择最佳方法可能是在实践中执行统计学习中最具挑战性的部分之一。
在本节中,我们将讨论在为特定数据集选择统计学习过程中出现的一些最重要的概念。随着本书的进展,我们将解释这里介绍的概念如何在实践中应用。
2.2.1 测量配合质量
为了评估统计学习方法在给定数据集上的性能,我们需要某种方法来测量它的预测与实际观测数据的匹配程度。也就是说,我们需要量化给定观测的预测响应值与该观测的真实响应值的接近程度。在回归设置中,最常用的测量方法是均方误差(MSE),由
在f (xi)是f对第i次观测的预测。如果预测响应与真实响应非常接近,MSE就会很小;如果对某些观测结果来说,预测响应与真实响应有很大差异,MSE就会很大。
(2.5)中的MSE是使用用于拟合模型的训练数据来计算的,因此更准确的称为训练MSE。但一般来说,我们并不真正关心该方法对训练数据的处理效果如何。相反,我们感兴趣的是,当我们将我们的方法应用于以前未见过的测试数据时,我们所得到的预判的准确性。为什么这是我们关心的?假设我们对开发一种算法感兴趣,该算法可以基于以前的股票回报来预测股票的价格。我们可以用过去6个月的股票收益来训练这个方法。但我们并不在乎我们的方法对上周股价的预测有多准确。我们关心的是它对明天或下个月价格的预测。同样,假设我们对一些患者进行了临床测量(例如体重、血压、身高、年龄、家族史),以及关于每个患者是否患有糖尿病的信息。我们可以利用这些患者来训练一种统计学习方法来预测基于临床测量的糖尿病风险。在实践中,我们希望该方法能够根据未来患者的临床测量准确预测其患糖尿病的风险。我们对这种方法能否准确预测用于训练模型的患者的糖尿病风险并不十分感兴趣,因为我们已经知道这些患者中哪些人患有糖尿病。
为了更精确地描述它,假设我们将统计学习方法与训练观察值{(x)相匹配1y1),(x2y2),hellip;hellip;(xnyn)},
circ; circ; circ; circ;
得到f的估计值,然后计算f(x1),f (x2),hellip;hellip;f(x)n)。如果这些近似等于y1y2hellip;hellip;yn,则(2.5)给出的训练MSE较小。然而,我们真的不感兴趣是否
circ; asymp; circ;
f(xiy)i;相反,我们想知道f(x0)近似等于y0,(x0y0)是一种以前未见过的测试观察,不用于训练统计学习方法。我们想要选择的方法,给予最低的测试MSE,而不是最低的培训MSE。换句话说,如果我们有大量的测试观测,我们可以计算
Ave(fcirc;(x0) minus; y0)2, (2.6)
这些测试观测值的平均平方预测误差(x0y0)。我们想要选择这个数量的平均值(测试mse)尽可能小的模型。
我们如何着手选择一个最小化测试MSE的方法呢?在某些设置中,我们可能有一个可用的测试数据集——也就是说,我们可能有访问一组未用于训练统计学习方法的观察值。然后,我们可以简单地对测试观察值进行评估(2.6),并选择测试MSE所使用的学习方法
图2.9。左:f模拟数据,黑色表示。三个估计
- 如图所示:线性回归线(橙色曲线)和两条平滑样条拟合(蓝色和绿色曲线)。右:训练MSE(灰色曲线),测试MSE(红色曲线),以及所有方法中最小可能的测试MSE(虚线)。正方形表示左图所示的三次拟合的训练和测试mse面板。
最小,但是如果没有可用的测试观测结果呢?在这种情况下,可以简单地想象选择一种统计学习方法来最小化训练MSE(2.5)。这似乎是一个明智的做法,因为培训MSE和测试MSE似乎密切相关。不幸的是,这种策略存在一个根本性的问题:不能保证具有最低训练MSE的方法也具有最低的测试MSE。粗略地说,问题在于许多统计方法都是专门估计系数的,从而最小化训练集MSE。对于这些方法,训练集MSE可以非常小,但是测试MSE通常要大得多。
图2.9用一个简单的例子说明了这种现象。在图2.9的左边面板中,我们从(2.1)生成了观察值,黑色曲线给出了真实的f值。橙色、蓝色和绿色曲线是对f值的三种可能的估计的错误,这些估计是通过增加灵活性的方法得到的。橙色线是线性回归拟合,相对不灵活。蓝色和绿色曲线是使用平滑样条生成的,在第7章中讨论了不同平滑程度的曲
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[426639],资料为PDF文档或Word文档,PDF文档可免费转换为Word


