
英语原文共 5 页,剩余内容已隐藏,支付完成后下载完整资料
用皮秒太赫兹脉冲将SrTiO3薄膜
由铁电软模式瞬时驱动到非谐振状态
I. Katayama,1 H. Aoki,2 J. Takeda,2 H. Shimosato,3 M. Ashida,3,4 R. Kinjo,5 I. Kawayama,5 M. Tonouchi,5M. Nagai,4,6 and K. Tanaka6,7,8
1Interdisciplinary Research Center,Yokohama National University,Yokohama 240-8501,Japan
2Graduate School of Engineering,Yokohama National University,Yokohama 240-8501,Japan
3Graduate School of Engineering Science,Osaka University,Toyonaka 560-8531, Japan
4PRESTO JST,Tokyo 102-0075, Japan
5Institute of Laser Engineering, Osaka University,Suita 565-0871, Japan
6 Graduate School of Science,Kyoto University, Kyoto 606-8502, Japan
7iCeMS, Kyoto 606-8501, Japan
8CRESY JST, Tokyo 102-0075, Japan
(2011年4月7日接收; 2011年10月2日接收修订稿;
2012年2月28日发表)
用强烈的皮秒太赫兹脉冲将SrTiO3薄膜中的铁电软模式脉冲驱动至大振幅。随着太赫兹电场的增加,软模吸收峰出现蓝移和光谱变窄。经典非谐振模型表明,诱导位移与铁电相变是相当的。光谱变窄表明位移超过膜中任何因不均匀性引起的位移,说明该方法可用于探测固有四次非谐性。
最新发展的超短激光脉冲技术成为研究凝聚态物质的相位和性质的相干操作的独特方法[1]。特别是由于固体中的离子和分子运动通常发生在皮秒时间尺度上,所以强烈的飞秒激光脉冲可用于有力地将这些运动驱动到远离热平衡的大振幅处[2]。这种机制有着广泛的应用,特别是在选择性化学反应[3]和宏观相的超快速相干切换[4]。
通常通过电子激发态或脉冲激发的拉曼散射过程可诱导大振幅振动[5,6],这是入射电磁场的二阶或更高阶过程。在这些过程中,激光脉冲电场的包络函数在材料中驱动皮秒振动。然而,由于振荡周期与时间尺度相匹配,驱动力与电场成正比,因此谐振低频电磁脉冲可以比超短光脉冲更有效地直接驱动红外激活模式下的大振幅位移。这种替代方案也可以对更清洁的实验进行更好的控制,即没有意外的电子激发(例如光致材料损坏)的实验。由于太赫兹区域存在与宏观相变相关的激发,因此我们正努力证明具有少量周期太赫兹脉冲的太赫兹诱导的宏观相变。进一步证明最近的理论预测:相控太赫兹脉冲激励可以翻转铁电极化[7]。事实上,有机晶体中分子内模式的软化已经被实验证明[8]。然而,这些系统中结构相变的巨大障碍需要太赫兹脉冲而不是电场。
然而,SrTiO3薄膜对铁电相变的势垒很低。这是因为SrTiO3中铁电相变的外推居里温度与太赫兹光子的能量相当[9]。众所周知,小扰动如来自外部电场,单轴压力或同位素或杂质替代的扰动会引起该材料中的铁电相变[10-12]。这种材料具有与这些特性有关的高度非谐振软模[见图1(a)],在低温下太赫兹区具有非常大的振子强度[13,14]。因此,它特别适合于铁电极化的相干控制的演示。
在这项研究中,我们专注SrTiO3薄膜的软模以展示大振幅铁电极化的相干驱动。我们的研究结果首次表明,激烈的皮秒太赫兹脉冲能够冲击性地将SrTiO3薄膜中偶极子允许的铁电软模式驱动到非谐区域,其振幅可以与预期的在扰动诱导的铁电相中的铁电失真相当。此外,软模的诱导位移似乎超过了薄膜中任何不均匀性所引起的位移。因此,这种方法可以定量地估计软模在低温下的固有不和谐性。我们的研究结果表明太赫兹脉冲对材料宏观相位的相干控制和非线性太赫兹光谱具有强大潜力。此外,非谐电势的评估对于理解铁电或量子顺电材料的晶格动力学和局部振动势是很重要的。
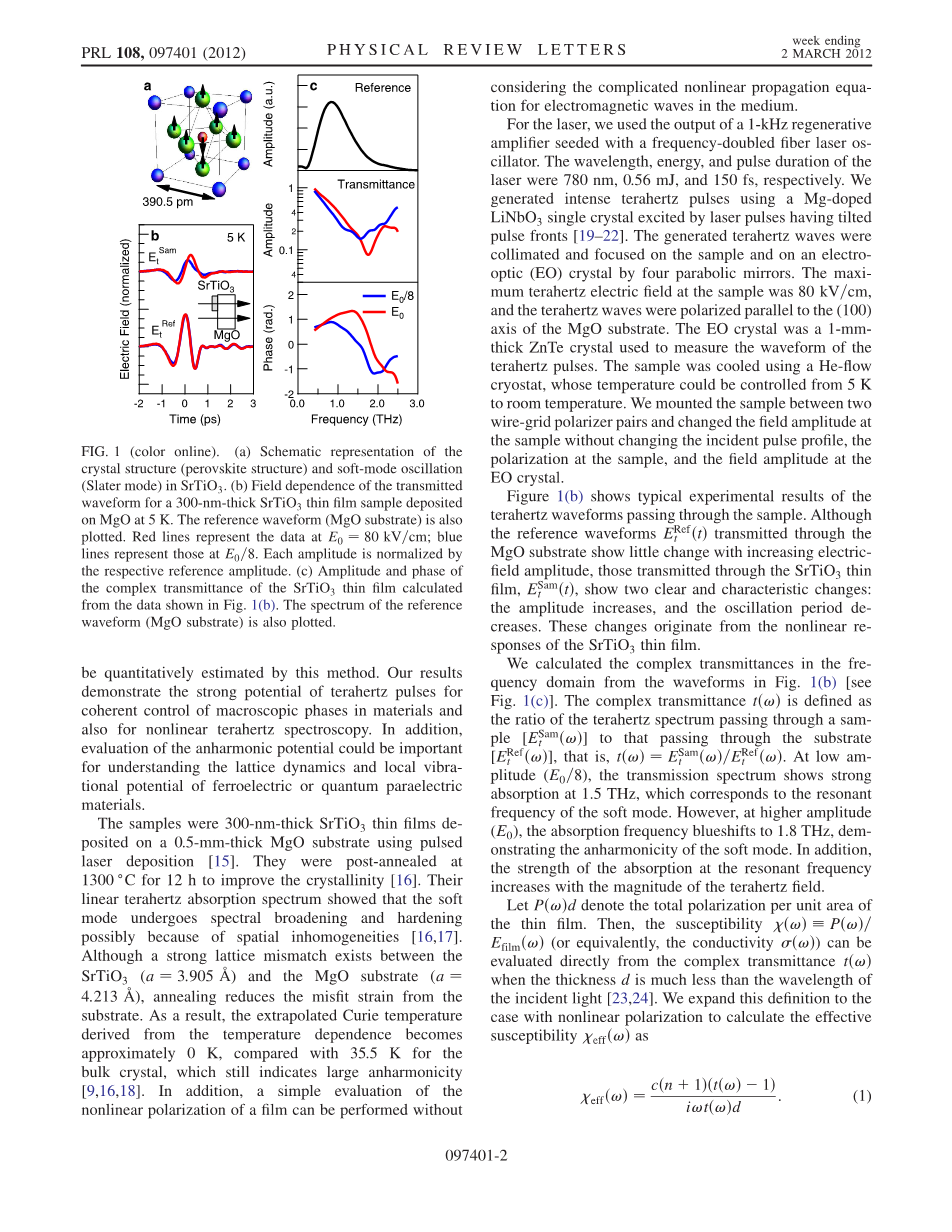
图1(a)SrTiO3中晶体结构(钙钛矿结构)和软模振荡(Slater模式)的示意图。(b)在5K下沉积在MgO上的300nm厚的SrTiO3薄膜样品的透射波形的场依存性及参考波形(MgO基底)。红线代表处的数据; 蓝线代表处的数据。每个幅度由相应的参考幅度归一化。(c)根据图1(b)所示的数据计算的SrTiO3薄膜的复合透射率的振幅和相位及参考波形(MgO基片)的光谱。
样品是采用脉冲激光沉积法在厚度为0.5 mm的MgO基片上沉积的厚度为300 nm的SrTiO3薄膜[15]。在1300℃后退火12小时以提高结晶度[16]。他们的线性太赫兹吸收光谱表明,软模经历光谱展宽和硬化可能是由于空间不均匀性[16,17]。尽管SrTiO3 ()和MgO衬底()之间存在强烈的晶格失配,退火可减少衬底上的失配应变。结果,由温度依赖性导出的外推居里温度大约变为0 K,而块状晶体则为35.5 K,这表明仍然具有大的非谐性[9,16,18]。此外,在不考虑介质中电磁波的复杂非线性传播方程的情况下,可以对膜的非线性偏振进行简单的评估。
对于激光器,我们使用了一个采用倍频光纤激光振荡器的1 kHz再生放大器的输出。激光的波长,能量和脉冲持续时间分别为780nm,0.56mJ和150fs。我们使用具有倾斜脉冲前沿的激光脉冲激发的Mg掺杂的LiNbO3单晶产生强烈的太赫兹脉冲[19-22]。产生的太赫兹波被准直并聚焦在样品上,并通过四个抛物面反射镜聚焦在电光(EO)晶体上。样品的最大太赫兹电场为且太赫兹波平行于MgO基片的(100)轴极化。EO晶体是1mm厚的ZnTe晶体,用于测量太赫兹脉冲的波形。使用He流动低温恒温器冷却样品,其温度可以从5K控制到室温。我们将样品安装在两个线栅偏振器对之间,改变了样品处的场振幅,不改变入射脉冲轮廓,样品极化和EO晶体的场振幅。
图1(b)显示了通过样品的太赫兹波形的典型实验结果。尽管透过MgO基片的参考波形随着电场振幅的增加而变化不大,但透过SrTiO3薄膜的参考波形显示出两个明显的特征性变化:振幅增大,振荡周期减小。这些变化起源于SrTiO3薄膜的非线性响应。
我们根据图1(b)中的波形计算了频域中的复数透射率[见图1(c)]。复合透射率被定义为穿过样品的太赫兹光谱与穿过基板的太赫兹光谱的比值,即。在低振幅时,透射光谱在1.5THz处显示强吸收,这对应于软模式的谐振频率。然而,在较高的振幅下,吸收频率蓝移至1.8THz,表明软模的不和谐性。另外,谐振频率处的吸收强度随着太赫兹场的大小而增加。
设表示薄膜的每单位面积的总偏振。然后,当厚度d远小于入射光的波长时,可以从复合透射率直接评估磁化率(或等效电导率)[23,24]。我们将这个定义扩展到具有非线性极化的情况来计算有效磁化率,及
(1)
这里,,,,和分别是角频率,基板的折射率,光速,真空的介电常数和膜内的电场。
我们研究了不同振幅的太赫兹波的实部和虚部(图2)。对于和,软模式的谐振频率几乎保持不变,但对于和则显示明显的高频移动。此外,吸收带宽随入射场振幅增加而减小。
随着温度的升高,已知SrTiO3中的软模由于软模和其他耦合模的非谐性和热波动而分别表现出高频移和光谱展宽[16,25]。在高电场幅度下观察到的这种高频偏移与软模频率的温度依赖性一致。然而,高电场幅度处的光谱变窄的趋势与软模频率的温度相关性所观察到的趋势相反。这一点特别重要,因为它表明太赫兹脉冲驱动软模不是其他模,而所有声子模在温度升高时均等地激发。这种有针对性的激发能力使得非线性太赫兹光谱成为研究太赫兹区域非谐性和非线性模式耦合的有效方法。
为了阐明非谐格子动力学,我们使用经典非谐振子模型[26]模拟了在强太赫兹电场下软模的非线性响应。这里,软模式在点被认为是单模,因为太赫兹脉冲具有比布里渊区中的多数点处的波矢小的波矢。软模式的阻尼常数中包含了由基片缺陷或应力引起的各个本地振荡器的不均匀性。我们考虑势能(即力的项)中的四次项,并在数值上求解方程以获得时间相关的极化。运动方程可写成
(2)
这里,,,,和分别是软模的谐振频率,四次非谐性常数,阻尼常数,有效质量和有效电荷。我们使用参考文献[27]和我们的样本观察到的软模振荡器强度[16]计算的有效电荷(e:电子电荷)和(m:质子质量)。
在薄膜近似中,软模的驱动力与薄膜内部的位置无关,因为电场可以看作是均匀的。因此,由[28]给出
(3)
这里,是入射的太赫兹电场,d是薄膜的厚度。设定谐振频率()和线性阻尼常数()以再现膜的线性介电色散,且被设置为适合光谱中的非线性变化。Q的初始位置是原点(Q = 0),它是SrTiO3中量子力学波动的平均值。有效敏感度可以从和的变换中计算出来。
该模型在高电场强度下显示软模的频移,而不是频谱变窄。这是因为即使包含四次非谐性,高阶阻尼项也不包含。因为SrTiO3具有反演对称性,所以最低阶非线性阻尼应与成比例; 因此整体阻尼常数变为。这里, 是阻尼常数对于小位移极限有效,而是现象学的非线性阻尼系数,其负号表示软模的频谱变窄。图2中的线显示了计算的实部和虚部具有四次非简谐性和非线性阻尼系数。图3(a)显示了用于软模式的电位。
图2 有效磁化率的导出实部和虚部。。 线表示使用具有四次非谐性和非线性失相的经典非谐振荡器模型的相应计算。箭头分别表示过零点和实部和虚部的峰值,分别对应于谐振频率。
局部振荡器共振中的不均匀加宽是由于来自衬底的空间相关力引起的。应力会引起局部离子位移,使得局部电位的二次项发生变化,从而导致线性光谱中观察到的不均匀变宽。负的非线性阻尼系数表明当软模的感应位移比由于不均匀性引起的位移大得多时,来自高次项的电位的贡献变为主导,并且电位的变化减小。如图3(a)所示,非均匀展宽在势能的最小值处较大,而在较大位移处则减小。
图3(b)表示了施加时的太赫兹波时软模的计算位移。计算结果表明,太赫兹脉冲相干驱动软模的位移为1pm,这只比BaTiO3(~10 pm)等相关铁电材料中的铁电相变相关的位移小1个数量级[29]。考虑到BaTiO3(393K)和SrTiO3(35.5K [9])的居里温度之间的差异,SrTiO3中微扰诱导铁电相的铁电位移预计会小于BaTiO3中的铁电位移。因此,诱导位移的幅度可以认为与SrTiO3中的铁电相变的幅度相当,能显示非谐性引起的非线性响应。
得到的四次非谐性常数可以与参考文献[30]中的热力学四次非谐性常数相比较,这是自由能(P是极化)中项的系数。从我们的实验中可得估计为,比参考文献[30]的值高1个数量级。造成这种差异的一个可能原因可以解释如下:虽然它们可以有助于减小热力学静态场实验的非线性,但它们的相互作用比太赫兹周期慢。软模态势中的高阶项也会影响我们实验中估计的四次非谐性值,因为我们在模拟中忽略了它们的简单性。这些结果表明,非线性太赫兹光谱是理解材料内在的非谐格子动力学不可或缺的工具。
图3(a)模拟中使用的非谐波软模电位的电位曲线。虚线表示谐波部分。位移决定了电位的宽度示意性地表示相应的移相速率。(b)计算的软模的位移。 用于计算的入射电场用虚线表示。
我们的研究结果证实,太赫兹脉冲驱动软模式的位移大于非均匀性引起的位移,并且观察到内在的不和谐性。由于这种方法可以探测固定温度下的固有非谐性,因此类似的铁电或量子顺电体晶体实验可以加深我们对软模的新型非谐格子动力学的理解,如量子顺电和量子铁电。此外,通过改变衬底调整SrTiO3薄膜的介电性能的能力可以研究包括双阱在内的各种可能形状的非线性动力学。
总之,我们证明了强烈的单周期太赫兹脉冲可以脉冲驱动SrTiO3薄膜中的软模偶极子发生大位移。由于非和谐性,软模式表现出非线性响应,即蓝移和光谱变窄。诱导的位移超过了由于薄膜中的不均匀性引起的位移,并且变得与扰动引起的铁电相变的相当。这些非线性响应可用经典的非谐振子模型来解释,从而可以定量测量SrTiO3薄膜中软模的强固有四次非谐性和非线性尼。本研究所表明的集体模式对非谐区域的连贯驱动可能为凝聚物宏观相位的一致控制开辟了一条有趣的新途径。
这项工作得到了教育,文化,体育和科技部通过KAKENHI(赠款第2110
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[462728],资料为PDF文档或Word文档,PDF文档可免费转换为Word


