英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
多铁性六方相HoMnO3中四方相互作用反铁磁共振的不对称分裂
N. J. Laurita,1 Yi Luo,1 Rongwei Hu,2 Meixia Wu,2 S. W. Cheong,2 O. Tchernyshyov,1 and N. P.Armitage1
1 The Institute for Quantum Matter, Department of Physics and Astronomy,
The Johns Hopkins University, Baltimore, Maryland 21218, USA
2 Rutgers Center For Emergent Materials, Department of Physics and Astronomy, Rutgers University, Piscataway, New Jersey 08854, USA
(Received 26 May 2017; revised manuscript received 10 October 2017; published 1 December 2017)
反铁磁共振(AFR)实验中两个自旋波分支的对称分裂一直是半个世纪以来反铁磁体的基本测量。在这项工作中,在低对称多铁六方HoMnO3上进行的圆极化时域THz光谱学实验揭示了 Mn亚晶格的AFR在施加的磁场中不对称地分裂,在高和低之间g因子asymp;50%的差异这种激发的 能量分支。 g因子的温度依赖性,包括在Ho自旋排序温度下的剧烈重整化,揭示了这种不 对称性明确地源于Ho-Mn相互作用。理论计算表明,AFR不对称性不能单独由传统的Ho-Mn交换机制来解释,只有在四次自旋相互作用也包含在自旋哈密顿量中时才会被再现。我们的研究 结果为六方锰氧化物和一般低对称反铁磁体的这种新型相互作用的光学研究提供了范例。
自从半个世纪前Kittel最早描述以来,反铁磁共振(AFR)一直是反铁磁性最重要的性质[1]。在AFR实验中,两个自旋波分支各自对圆偏振光的不同螺旋性起作用,在施加的磁场中对称分裂。然而,这种现象的变化可能发生在低对称环境中,因为磁绝缘体中局部自旋之间的相互作用很大程度上受到它们嵌入其中的晶体结构的对称性的影响。六方稀土亚锰酸盐(h-RMnO3)是低对称性导致显着物理性能的材料的主要例子[2],包括多铁性和特别强的磁电耦合[3]。这些系统中的磁性由稀土锰磁矩组成,这些磁矩由于晶体各向异性而位于正交方向[4]。这些时刻之间的相互作用一直是一个激烈的调查的主题[4-8],因为这种耦合被认为是驱动磁转变[9]和介导磁电现象[10,11]。然而,R-Mn自旋之间的交换机制仍然难以捉摸,因为它们的正交性表明在平衡自旋构型中比常规相互作用少海森堡交换。
图1: HMO在铁电相(T lt;Tc = 875K)中的晶体结构分别沿(左)c轴和(右)轴观察。 在这个阶段,Ho 3离子(绿色和蓝色球体)位于晶格的对称不同位置,导致沿着c轴的有限的铁电矩。
在这些材料中,六方晶系HoMnO3(HMO)具有最大的有效稀土磁矩,因此它是理想的研究这些系统中磁交换的材料[3,12-15]。 HMO的六方晶体结构(图1)由沿着c轴层叠的角共享MnO5双锥体和Ho离子组成[16]。在铁电跃迁Tc = 875K时,MnO5双锥带扣[17-19]减小了非中心对称极性空间群P63cm的对称性,其中Ho离子占据了晶格的两个对称不同位置。 SMn = 2自旋形成一个二维受挫三角格子,其在120°asymp;120 K的结构中的TNasymp;75 K,对称性为P60 3c0 m [20-25]。在TSRasymp;40K(P603cm0)和THoasymp;5K(P63cm)时出现两个额外的零场Mn亚晶格跃迁,其中Mn自旋在基面内旋转90°。 Ho子格的排序不太清楚[4,20-27];然而,由于单轴各向异性[4],预计SHo = 2自旋沿c轴反铁磁性排列,实验证据表明至少有一个Ho子晶格在TSR附近开始起磁[4,27]在THo以下存在的远程命令。
可以通过检查Mn亚晶格的自旋激发来探测六方锰酸盐中R和Mn矩之间的相互作用,其最小自旋哈密顿量由下式给出:
其中J是海森堡交换,Delta;是平面各向异性,B∥c是外加磁场,g = 2是Mn g因子,总和在相邻对上[23,28]。 锰亚晶格的基态是120°有序的AF。 在k⃗→0限制(适用于我们的光学测量)中,低能谱由Goldstone模式和AFIP [28]组成。 在弱磁场极限下,对HMO中的磁场H lt;SMnJasymp;40T有效,AFR的能量由下式给出
揭示了两种模式,它们在场中对称分裂,其中geff = g = 2 4Delta;= 9J [29] [见方程(8-12) III在补充材料(SM)中的推导[30]]。请注意,即使对于小的各向异性,geff大约是裸露离子值的一半。这是120°有序自动对焦的一个特征,它由于有序状态的低对称性而产生,导致未定义好的角动量量子数。在HMO [23]中,我们发现交换和各向异性分别为J = 2.44meV和Delta;= 0.38meV,我们期望Eq。= 0.97。 (2)。然而,实际上在六角形锰矿的低温下观察到更大的g因子[7,29]。这可以通过引入一个额外的海森堡交换相互作用来解释,该相互作用将R自旋与Mn AFR模式的有限Sz铁磁耦合成Eq。 (1)[7]。然而,由于自旋的正交性,这种耦合预计会在基态中消失,从而导致主要平衡R-Mn自旋相互作用未被解决。
在这封信中,我们通过高分辨率时域太赫兹光谱学(TDTS)对HMO的低能光学响应进行了系统研究。 我们证明Mn AFR对圆偏振光具有不同的选择规则,这使得我们的实验能够以高精度解决AFR在弱磁场中的场依赖性分裂。 发现AFR意外地在磁场中不对称分裂。 仔细研究这种不对称的温度依赖性明确证明了R-Mn相互作用的影响。 理论研究得出的结论是,不对称性不能单独由传统的R-Mn交换机制来解释,只有在自旋哈密顿量中也包括新的四次自旋相互作用时才会被重现。 讨论了其他六方锰矿中这种相互作用的可能性。
通过光学漂浮区法生长单晶HMO。 两个样本的方向[-1;1; 0](d = 670mu;m)和[0,0,1](d = 590mu;m)。 TDTS传输实验使用自制的光谱仪[31]在高达6T的法拉第几何磁场中进行()。 通过将太赫兹场耦合到样品的电偶极子跃迁,TDTS以0.2-2 THz的超高分辨率访问样品的电磁响应。
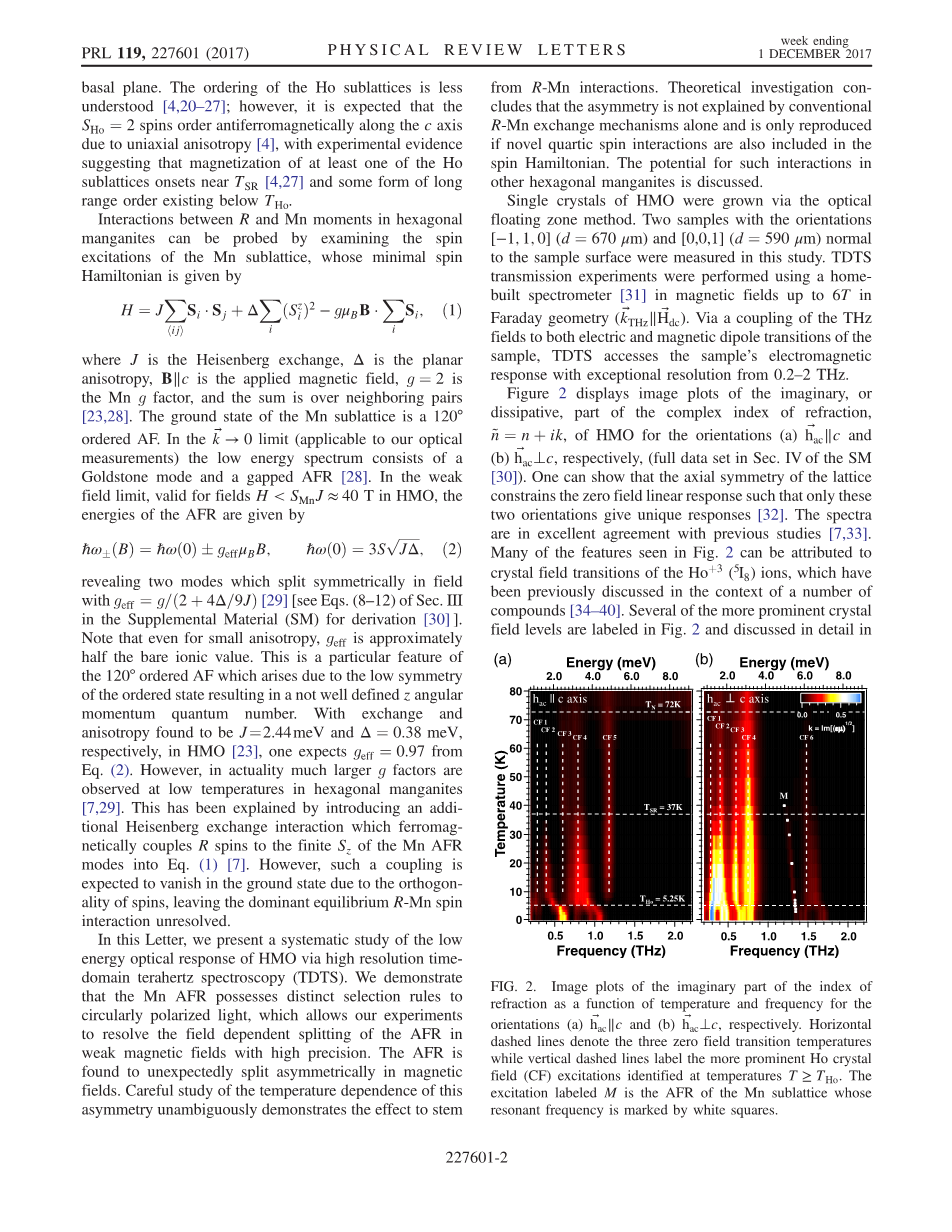
图2:折射率的虚部分别作为方向(a)h⃗ac∥c和(b)h⃗acperp;c的温度和频率的函数的图像。 水平虚线表示三个零场转换温度,而垂直虚线标记在温度Tge;THo时识别的更显着的Ho晶场(CF)激发。 标记为M的激发是Mn子晶格的AFR,其谐振频率由白色方块标记。
图2分别显示了定向(a)和(b)的HMO的复折射率的虚部或耗散部分的图像图,其中n = 1 / n ik, (SM [30]第四节中的完整数据集)。人们可以证明,晶格的轴对称性约束了零场线性响应,这样只有这两个方向才有唯一的响应[32]。光谱与以前的研究非常吻合[7,33]。图2所示的许多特征可归因于(5I8)离子的晶体场跃迁,这在以前的一些化合物中已有讨论[34-40]。在图2中标出了几个更突出的晶场等级,并在第2节详细讨论。 SM的IV(见表I)[30]。突然发生的光谱变化,包括先前未发现的晶体场激发能量在asymp;5K处的戏剧性重新正常化,确定了在TN = 72 K,TSR = 37 K和THo = 5.25 K时的三个零场磁转变。在这里,我们注意图2中标记为“M”的Mn亚晶格的AFR。为了提取该模式的动力学性质,使用Drude-Lorentz振荡器在线性背景上拟合光谱以解释相邻的晶体场水平。图2中的白色方块表示Mn AFR的提取共振频率。
然后作为磁场的函数进行测量以研究AFR的场依赖性分裂。 HMO的六角形对称性和T对称性在外加场下的断裂约束了线性响应传递矩阵[32,41],使得它必须在线性基础上完全反对称
这种完全反对称的传输矩阵可以通过循环基变换来对角化
其中T_1和T_r分别指左旋和右旋圆偏振光的透射,即本征偏振。 上述分析表明,在法拉第几何中执行的实验可以在循环基础中得到最好的理解(参见SM的Sec I.了解更多细节[30])。 此处执行的TDTS测量采用旋转偏振器技术,可以同时测量样品对两个偏振方向的响应,从而可以转换为圆形基准[42]。
图 3:在20 K时,HMO的折射率虚部的场依存性(a)右手和(b)左手圆偏振与H∥c。 Mn AFR是在asymp;1.3THz时线性变化的激励,可以看出其在循环基础上自然划分为低能量和高能量分支。 白色三角形表示AFR提取的共振频率。
图3(a)和3(b)分别显示了折射率耗散部分的图像曲线,其分别针对右侧和左侧圆偏振为20 K时的磁场的函数。 在asymp;1.3THz随着磁场线性变化的激发是Mn亚晶格的AFR。 可以立即看到AFR的两个分支对右旋和左旋圆极化具有不同的选择规则。 AFR的这种划分允许在HMO的低场“中间”阶段中在弱磁场中独立访问该模式的分裂,其中两个分支否则将在线性基础上高度重叠。 以与零场数据类似的方式,这些光谱适合于提取AFR的依赖于磁场的动力学特性。 图3中的白色三角形表示AFR在其定义明确的区域的共振频率。
通过将提取的谐振频率作为磁场的函数进行拟合,可以找到AFR的g因子。重申一下,方程式的期望。 (2)是g因子asymp;1的两个分支的对称分裂。图4(a)显示了弱磁场下AFR共振频率在HMO的低场相位内的线性拟合。人们可以看到,g因子不仅很大,而且出乎意料地是不对称的,低能量分支拥有比高能分支大约50%的g因子。这种不对称还延伸到负场,因此低能量分支总是具有更大的g因子。数据的一个显着方面是R和L分支中的扭折作为B零点附近的函数。我们认为,这种不分析性是由下面讨论的基于磁场符号变化选择基态的方式产生的。低能量分支在正负电场之间的g因子的小差异可能源于负电场中由于AFR较弱而导致的较大误差线。虽然通过R-Mn自旋相互作用解释了增强的g因子[7],但AFR的场依赖性分裂中的不对称之前尚未报道过。
图4:(a)左旋(蓝色,圆形)和右旋(红色,方形)圆极化的AFR的谐振频率作为T = 20K时的磁场的函数。 无论极化和场方向如何,AFR都具有比高能分支大得多的g因子。 (b)g因子的温度依赖性显示了THo显着的重整化。 (c)绘制的g因子的不对称比率与Delta;x,减去了顺磁贡献之后的H∥c磁化率。
我们可以通过检查g因子的温度依赖性来确定这种不对称的起源[图4(b)]。 g因子随着温度的降低而增加,这种趋势与其他六方锰氧化物一致[29]。然而,在HMO中,我们观察到在THo处的g因子的大量重整化,分别在右手和左手分支中从30K增加到THo的约50%和35%。这种效应可以归因于THo附近的有效内场的大量增加,因为Ho子晶格在转变附近更容易被磁化,这与在THo处的磁化率的观察到的峰值一致[图7]。 4(c)] [2]。在转换之下,Ho子晶格假定为AF有序,内部场减少,g因子返回接近其高温值(尽管由于与邻近的Ho晶场等级重叠,2K处的误差棒较大)。图4(c)显示了非对称比率,其中定义为:在减去顺磁贡献之后,HMO的H ||c磁化率与Delta;chi;一起被定义为。我们可以将这种敏感性归因于Ho磁性。可以看出,不对称比率的温度依赖性与磁化率显着一致,在TSR以下增加,在THo重新正常化,在较低温度下迅速降低。这样一个阴谋清楚地表明g因子不对称与Ho-Mn相互作用有关。
为了研究这种不对称的起源,我们探索了一个场景,其中顺磁Ho矩在锰场上产生有效的交换场。 为了使两个AFR分支向下倾斜,该交换场Heff必须与Mn矩反向平行,从而降低了与有序状态的小偏差的成本。 与此同时,它是通过波动Ho矩来产生的,它们的热平均值与施加的场B和Ho磁化率成正比,随着温度朝向Ho处的Ho排序降低而增加。 在这种情况下,方程的交换和各向异性。 (2)被修改,使得它们在B上线性依赖
然后,对于线性顺序,AFR的能量是
并且斜率domega;= dB的幅度可能不同。
来自Ho自旋沿c轴偏振的ab平面中的这种交换场可以来自Dzyaloshinskii-Moriya(DM)相互作用,HDM = D·SHotimes;SMn,在ab平面中具有DM向量D [43,44 ]。虽然我们认为这个DM术语在这里扮演了一个角色,但在最直接的情况下,这导致了相反的效果:两个AFR分支都向上倾斜。为了理解为什么,注意到有效交换场Heff = -Dtimes;hSHoi打破了哈密顿量(1)中ab平面旋转的全局对称性。 Mn自旋定向为与Heff平行以最小化DM能量并选择基态。一般来说,正是这种基态的变化随着磁场方向的变化而导致R和L激发在B = 0附近的不可分析性。与这些优选方向的偏差现在耗费了额外的能量,这导致两者都硬化AFR分支与实验观察相反。我们发现其他类型的相互作用破坏了选择基态的全局旋转对称性,一般都会硬化两个AFR分支[30]。为了获得软化,必须具有DM相互作用和强制各向异性在平面中的四次相互作用的组合效应。例如,交互
之前已经被提出来驱动HMO中的磁转变[9]。 然而,其他对称允许的四次项也可以再现AFR中观察到的不对称性(参见SM [30]的第三节)。 当存在两种扰动时,可以选择基态,而另一个决定导致净软化的硬模的刚度。 这是一种通用机制,可能导致其他系统中的gfactor不对称。
综上所述,高精度时域THz实验揭示了多铁HMO中Mn亚晶格的AF
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[462722],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。