
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
具有混合共振的声学超表面
阻抗匹配表面具有入射波不产生反射的特性。我们在此证明,通过使用一个简单的结构,声波反射面可以获得混合共振,并在可调频率下成为与空气中的声音相匹配的阻抗,这样就不会产生反射。超表面的每个共振单元在所有空间维度上都是深亚波长,其厚度小于峰值吸收波长的两个数量级。由于不能传输,因此阻抗匹配的声波要么在一个或多个频率被完全吸收,要么转换成其他形式的能量,如电流,可实现23%的声电能量转换效率。
深亚波长尺度的理想吸收体具有重要的科学和工程意义。它可以作为点源的精确时间反转对应物,这对时间反转波技术有重要意义。传统的吸声方法是使用多孔和纤维材料和梯度折射率材料,或者使用穿孔或微穿孔板,这些板后面有调谐的空腔深度。它们通常导致要么阻抗与入射波不匹配,要么尺寸与波长相当的庞大结构。空间螺旋结构是潜在可行的方法来降低几何尺寸,但面临的挑战阻抗不匹配的背景介质。另一方面,主动“吸收器”则需要昂贵而复杂的电气设计。最近,有研究表明,对于电磁波,在两种不同材料之间构造界面可以导致具有不同功能的超表面,如相位不连续、异常折射/反射和极化操纵。特别是“相干完美吸收器”(CPA;参考文献17)在光学中通过依赖相位匹配(干扰)的反向传播的波在一个有损耗的材料。然而,要将这一概念应用到声学中,要么需要声学厚度较厚的材料,要么需要亚波长但耗散度高的平板(如用于电磁波的金属),这两种材料都不适用于低频声音。此外,所有这些机制都需要特定的粘性特性或精确的Q因子值才能获得最佳的吸收性能,这使得它们的鲁棒性较差,也很难调整。
在这项工作中,我们提出了在一个横向尺寸为深亚波长的薄弱吸收层中创建两个共振,然后通过将该层放置在一个坚硬的反射表面附近,并由一薄密封气胞隔开,从而使两个共振杂交的想法。杂化共振可以有两个有用的自由度,继承于两个原始共振,表现为其(空间变化的)向层方向位移的平均值和方差。虽然方差分量与辐射模(即聋模)解耦(见下文),但它具有吸收功能,而平均位移分量可调到与背景介质阻抗匹配。最终的结果是一个点状的声阱,它不需要像CPA中那样需要两个反向传播的波,并且是稳健的并且容易制造。声学超表面可以实现为这样的声汇的平面阵列,并具有附加的声-电换能器功能。下面我们将介绍这一想法的实现和理论,其中的薄层是一种膜型声学超材料。
装饰薄膜谐振器
由各种形式的装饰膜谐振器(DMRs)组成的膜型声学超材料已经被研究过。众所周知,几乎完全的传输发生在共振频率,而与入射波的解耦发生在所谓的反共振,从而导致全反射。用耦合膜结构也可以实现负声折射率。此外,人们可以通过在非对称形状的平板周长集中曲率能量,在谐振频率达到非常高的声吸收。然而,以前的研究都没有预料到以下现象或混合共振。
超表面单位细胞和总吸收
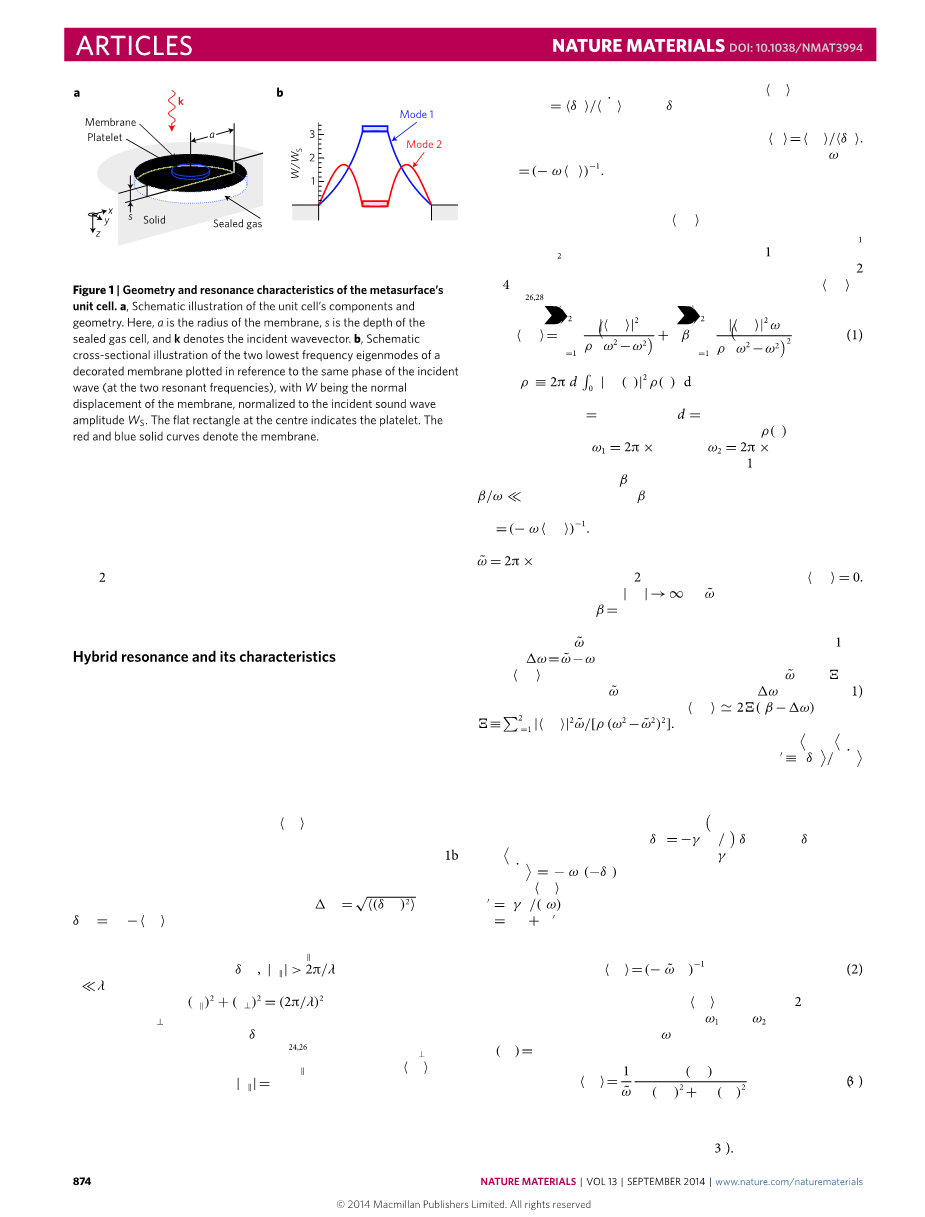
图1a说明了单元的几何形状。它由三部分组成:一个DMR,一个反射面,以及中间一层薄薄的密封气层。DMR由均匀拉伸的弹性膜组成,其半径为a=45 mm,厚度dle;0.2 mm。用半径r = 10 mm,质量m=0.8 g的血小板装饰。膜的边界固定在刚性框架上。DMR的最低本征模以中枢血小板在112 Hz时的振荡为特征;888 Hz的第二特征模的特征是周围膜的振荡,血小板几乎是稳定的(图1b)。作为反射面的铝背板与DMR通过深度s = 17毫米的间隙分开,在大气压力下密封一薄层气体。气体选择为六氟化硫(SF6;绝热指数小,见下文)。我们测量了超表面的一个单元格的吸收系数,如图2a所示,作为频率的函数。在152hz处有一个非常明显的吸收峰,吸收系数gt;0.99,这意味着与空气阻抗完全匹配。考虑到超小的细胞厚度,这是特别值得注意的,其中在152赫兹时空气的波长。
吸收峰的宽度非常小,为1.2 Hz,这是材料的低耗散系数的特点。这使得我们的吸声机制与传统的使用有损材料吸声的方法不同。令人惊讶的是,吸收峰与DMR的本征频率都不重合,而是位于其反共振附近。如图2a所示,图中两个箭头标记了DMR的第一特征模的频率和抗共振。下面我们证实这样一个非凡的吸收峰是混合共振的结果。
混合共振及其特性
气体和反射面有效地串联给DMR增加了额外的阻抗,从而改变了它的谐振条件。上述的DMR本征模被迫杂化形成新的共振模,位于前一组本征频率之间。这种混合共振很大程度上是两个相邻原本征模的线性叠加,因此保留了它们的特性。
理解混合模式的行为和功能的核心是,只有平均膜位移lt;Wgt;的活塞样分量与传输和反射耦合。这里W表示膜的法向位移,它是位置的函数,如图1b所示为两个共振特征函数,角括号表示膜面积的平均。然而,位移的方差定义为,其中,与辐射模式解耦,因此可以被描述为“聋”。解耦的原因可以从傅里叶波向量中看出,描绘了W对于,的横向空间模式。由于位移连续性条件和波动方程,我们有对于空气中的声波,表示垂直于膜的波向量分量。因此,位移的delta;W分量只对消失的波配对,因为其相关的一定是假想的,相反,因为lt;Wgt;的分量的分布在,它可以耦合辐射模式,即反射波和透射波。因此,如果我们只考虑辐射模态,那么我们就可以把声波超表面的问题本质上看成是一维的。为了与空气的表面阻抗相匹配,只需用给出的lt;Wgt;分量来定义表面阻抗,delta;p表示声压变化,过点表示时间导数。注意,表面平均绿色函数是由定义的。因此,对于角频率omega;的时谐运动,我们有。
为了解释混合共振的出现以及它是如何与空气声阻抗匹配的,让我们首先考虑DMR的表面平均绿色函数。为简单起见,我们只考虑图1b中DMR的前两个最低频率特征模W1(蓝色)和W2(红色)(图2和图4中的数据计算中包括高阶模态,并与实验进行比较),因此由下公式给出
其中是一个与膜的位移加权质量密度对于本征模,a = 45毫米,d = 0.2毫米表示半径 和厚度,rho;(r)是局部的质量密度,omega;1= 2pi; times; 112 Hz,omega;2= 2pi; times; 888 Hz是相关角本征频率。等式(1)假设耗散系数beta;较小,因此无量纲值将通过拟合来确定实验。DMR的阻抗由给出。
我们可以定位DMR的反共振频率,,介于两个特征频率之间(由图2a中的箭头所示),使用条件。这是很明显的,因为在omega;上,如果系统没有耗散—即beta;=0—意味着从入射波解耦。考虑到混合共振频率总是接近于,我们想通过将作为一个小参数来进一步简化方程(1)。我们表示关于频率的导数为。通过将它围绕omega;扩展到中的一阶,公式(1)可以简化为如下形式,其中。
薄膜的两个本征模被密封的气体层杂化,这增加了一个额外的阻抗的系统。由于密封气体的厚度小于相关波长的数量级,可以认为密封气体在膜的运动过程中经历了均匀的绝热压缩和膨胀,因此有,为位移的连续性(其中lt;Wgt;是沿着入射波的方向),我们获得,堆叠系统的总阻抗为,所以整个系统的绿色函数是
通过检验式(2)中lt;Ghgt;的虚部,很容易看出,在omega;1和omega;2处的原始共振被omega;h处的新的杂化共振所取代,并以条件Im(Zh)=0为特征,因此
达到一个高峰。绿色函数虚部的峰值表示为(共振)模式。这里,它正是如式(3)所暗示的混合共振。
由于Zh的虚部在混合共振处,因此有可能实现与空气阻抗Z0的完美匹配。有关条件如下:
这里,。尽管材料耗散系数beta;不能轻易调整,但由于我们还有另外两个参数macr;s和,这两个参数可以轻易调整来满足式(4)和(5),所以这种混合阻抗匹配条件仍然是稳健的。
基于DMR的前四个特征函数,求出了无量纲= 0.59。在图3a中,我们将macr;beta;(黑色曲线)和macr;s(红色曲线)作为的函数来满足阻抗匹配条件。特别是=0.065(用箭头表示)对应于处的阻抗匹配。通过计算拟合的耗散系数macr;beta;=0.00502 (beta;=5.14 Hz),可以预测SF6 (gamma;=1.0984)气层厚度为macr;s=0.0772 (s=17.2 mm)。后者与实验值s=17 mm非常一致。我们在这里要注意的是,在本实验中选择SF6是因为它的绝热指数较小,与空气(gamma;=1.4)相比,它将s降低了约27%。根据反射系数R=(Z0minus;Zh)/(Z0 Zh),我们可以计算出吸收系数为1minus;|R|2,如图2a中的黑色曲线所示。与实验结果一致。
通过聋组件的消耗
我们的实验结果表明,实现完全吸收只需要较弱的材料耗散(小macr;beta;),这可能有点令人惊讶。原因是膜位移的方差分量是聋的,可以变得非常大。当一个小的吸收系数乘以一个大的能量密度时,产生的吸收仍然是可观的。在图3b中,我们将计算的绘制成的函数。与我们的期望一致,的大小被认为在处发散,在这一点上,macr;s和macr;beta;都接近于零。这可以通过认识到混合模式仍然保留两个膜特征模的特征来理解,因此在omega;h(接近omega;)下,两个DMR模式lt;W1gt;和lt;W2gt;的振幅大小一定是可以比较的,即lt;W2gt;/lt;W1gt;asymp;1。而阻抗匹配则是lt;W1gt;minus;lt;W2gt;=lt;Whgt;=WS。这俩个条件只有当才能满足,因此,是一个较小的值。
为了进一步证实上述分析,我们测量了装饰膜在总吸收频率下的振动剖面。归一化为入射声振幅为1Pa(对应94 dB)的实验结果如图2b所示,用红色圆圈表示。这个混合共振剖面显然是膜的前两个本征模的线性叠加。在同一图中,我们展示了数值模拟的结果,与实测剖面非常一致。
从测量的位移,我们可以得到,接近Ws= 2.5micro;m的入射声幅值,明显的阻抗匹配证据。但是lt;Whgt;比血小板最大位移小一个数量级(超过40micro;m)。我们也可以从测量数据中推断出,这与图3b(用箭头表示)所示的关系是一致的。这种在反共振频率附近显著放大的位移分量解释了弱损耗膜的总吸收功能,并将我们的超表面与CPAs:这里的能量耗散集中在薄膜的横向尺寸,而CPAs是严格的一维特征,在其中波耗散时,它们反向传播和干涉沿传播方向。这里的耗散系数macr;beta;很小,在混合共振时血小板的最大位移非常大,从而能够完全吸收传入的声音。特别地,我们希望证明如此大的位移也使我们的超表面能够通过压电或电磁感应有效地将声能转换为电流。
声-电功率转换
声电能量转换是人们关注的热点。应用范围从传感器,执行器和传感器,功率扫选和功率转移。混合模式的阻抗匹配能力,加上与大相关的受限能量,使超表面成为能量转换的优秀候选材料。电磁感应、压电和摩擦带电通常用于这类任务。后两种选择需要精密的微/纳米加工。在这里,我们选择用一个简单的反扬声器设计来演示,以提取功率。图2c的插图显示了该装置的照片图像。磁铁线由一个薄的塑料框架支撑,塑料框架粘在中心的血小板上。四对钕磁铁沿磁力线放置,产生垂直于磁力线和血小板运动方向约0.6 T的磁场。磁场内导线的总长度为80毫米。在这个简单的装置中,中心血小板携带着导线,沿着垂直于磁场线的方向,呈活塞状上下摆动。根据法拉第定律,我们预期导线中会产生振荡电流。声能就这样转化为电能。在1 Pa的入射声波下,在混合共振处获得了超过1.5 mV的电动势(EMF),如图2c所示。由于与中心血小板相连的导线和其他外围设备的额外质量约为7.8%,混合谐振频率略降至147赫兹。总共是0.6负载的入射声功率为17micro;W,产生的电力为3.9micro;W。因此,功率转换效率为23%。这种效率在入射声强(2.5 mPa-4 Pa)的三个数量级变化中保持不变。进一步提高转换效率可以通过更复杂的设计来实现,使用更强的磁铁和更长的导线,以及更好地优化与负载匹配的电阻抗。
多个频率下的总吸收
我们的超表面也能够在多个位置进行统一吸收频率。这可以通过制造一个用于在多个频率下的吸收,其中每个细胞包括三个混合谐振单元。由于实验的限制,所有装置的横向尺寸均为a=17 mm,且r=3mm血小板装饰,1号机组m=0.18g,2号机组0.12g,3号机组0.06g,因此每个机组都能从另外两组里得到一个不同的omega;h。每个单元电池都有自己的密封气腔,在常压下充满SF6。机组1的气层厚度为30mm,机组2的气层厚度为25mm,机组3的气层厚度为15mm。在图4中,测量的吸收光谱被绘制成频率的函数。在255,309和420赫兹观察到总吸收。因为这三个单元平行地面对入射波,所以这三个单元的总阻抗可以简单地类比于电路中的三个平行阻抗: Z3-1。由于非常尖锐的混合共振剖面,很容易看到1/Zi必须迅速从处迅速消失,因此,在失配共振的情况下,这三个单元可以有效地隔离。应该注意的是,由于每个混合共振的高密度态,吸收截面几乎是每个单元几何截面的9倍。此外,由于超表面的功能是基于与胞体的局部混合共振,而胞体的横向尺寸远小于入射声波的波长,因此其特性基本不会随声波的入射角而发生变化。因此,由阻抗为Zi的单元阵列组成的超表面的性能可以从1/Zi的求和中预测出来。
总结
我们报道了一种声学超表面,它采用了一种新型的混合共振来实现鲁棒阻抗匹配和完美吸收。其单位细胞的深亚波长规模使得每个细胞本质上都是一个点声接收器,相当于一个点声源,时间反转。它非常窄但可调的总吸收带宽在频率选择应用中也可能是有利的,如滤波器,传感器和换能器。将这一概念扩展到其他流体介质中的声波应该是直接的,并可能导致在超声波、水声学和弱声探测方面的应用。当与现有技术相结合,如压电MEMS和纳米线器件,摩擦电器件,微机械换能器,声非接触能量传递器件和声显微镜,它的简单结构也提供了相当大的应用潜力。
研究方法
实验:超表面的基础是由铝精密加工而成。由于受阻抗管直径的限制,图2所示的结果仅为超表面的一个单元;对于图4所示的结果,超表面由三个横向尺寸减小的单元格组成。用改进的阻抗管法测
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[258865],资料为PDF文档或Word文档,PDF文档可免费转换为Word


