
英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
高压下硅的Si-I相和Si-V相的声速和弹性模量测量
摘要
文献采用皮秒激光超声技术,测量了金刚石压腔(DAC)中压缩样品的纵波声速随压强的变化关系。实验对较低压强下具有立方结构的Si-I相和较高压强下具有简单六方结构的Si-V相进行了研究。对于Si-I相,实验测量了0~9 GPa压强范围内单晶硅中沿晶向上的纵波声速。在Si-V相中,我们首次测量了在18~27 GPa压强范围内各向同性多晶状态下样品的平均声速。随着压强进一步的增高,由于具有简单六方结构的Si-V相晶粒会出现择优取向,从而阻碍了进一步的的测量,这些晶粒的c轴平行于DAC的压缩方向和声脉冲传播方向。本文推导出的Si-I相在不同压强下单晶弹性常数和与先前报道的Si-I相的结果非常一致;多晶状态下的Si-V相的剪切模量与我们利用第一性原理计算的结果吻合得很好。
正文
硅由于其在常压下的化学、物理和技术特性,在半导体领域得到了广泛的应用,成为半导体的基本材料。在压缩过程中,硅会金属化并经历一系列相变,因此被认为是压力诱发相变的一个例子。在过去的几十年中,晶体结构、相稳定性和相关的晶格动力学特性一直是实验和理论研究的热点。X射线衍射研究结果表明,随着压强的增大,硅的有序结构转变为:cubic-diamond(Si-I)→beta;-Sn (Si-II)→Imma (Si-XI)→primitive-hexagonal (Si-V)→Cmca (Si-VI),Si-II相、Si-XI相和Si-VI相在较窄的压力区域内稳定,由于与相邻相共存,在更窄的区域内以单相形式存在。相反,Si-I相、Si-V相、Si-VII相和Si-X相在扩展的压力范围内以单相形式存在。结果表明,Si-I相在Plt; 9 GPa时保持稳定,在18-38 GPa之间,仅观察到Si-V相。大多数关于硅的实验高压研究都集中在相的晶体结构上,但只有很少的工作涉及Si-I相的弹性模量的压力依赖性,而且据我们所知,至今没有测量剪切模量G或者单晶的弹性常数的工作被报道。
了解固体在高压下的声速可以更好地理解其固有的弹性特性,特别是G(P),它对细微的相变、缺陷或非均匀性非常敏感,并允许对非均匀体进行富对比度的三维断层扫描。然而,即使使用标准的超声波技术或更先进的同步辐射散射技术,在高压下测量声速也是具有挑战性的。相比标准超声技术适用于有限的压力范围,非弹性X射线散射允许测量压缩在DAC中非常高的压强下样品的纵波声速。然而,它需要使用同步辐射、大的设置以及非常长的计数时间,并且只适用于含有Z在30到50之间的元素的样品。核共振非弹性X射线散射的相关技术需要含有Mouml;ssba-uer同位素的样品和理论模型,以便从记录的信号中提取声速。因此,最后两种技术都不适用于DAC中硅样品的声速测量。当压强超过20 GPa时,DAC与皮秒激光超声(PLU)相结合可以获得不透明固体(如硅)的声速。最近,基于声子成像的PLU被证明可以提取一套完整的压缩在DAC中的Si-I相的弹性常数。然而,当加载条件变为非静水状态,且样品表面的变形严重影响声子成像的干涉检测时,这种方法的精度较低。此外,声学映射分析需要单晶,这些单晶在超高压和相变条件下很难保存。
泵浦-探测技术称为时域布里渊散射技术,可以应用于测量有半导体特性的Si-I相的,压强低于9 GPa时,波长的激光有着相对较长的光学穿透深度。然而,Si在1atm或者更高的压强下,在TDBS实验中,没有频率超过78 GHz的布里渊振荡现象观察到。因此,基于脉冲回波法的PLU可以被应用于测量Si-I相和Si-V相的。超快声脉冲产生和他们到来的检测由一个传统的PLU设置配备一个稳定的迈克尔逊干涉仪来完成。简单来说,一个锁模钛蓝宝石激光(美态光谱,)操作的重复频率为80MHz,它的脉冲宽度的lt;100 fs,分为泵浦光束和探测光束。泵浦光的光子频率增加了一倍,以保证在硅材料中有效地产生声脉冲。然后将光束聚焦在样品的相对侧面,用times;50的显微镜物镜聚焦到直径为2毫米的斑点上。(图1)
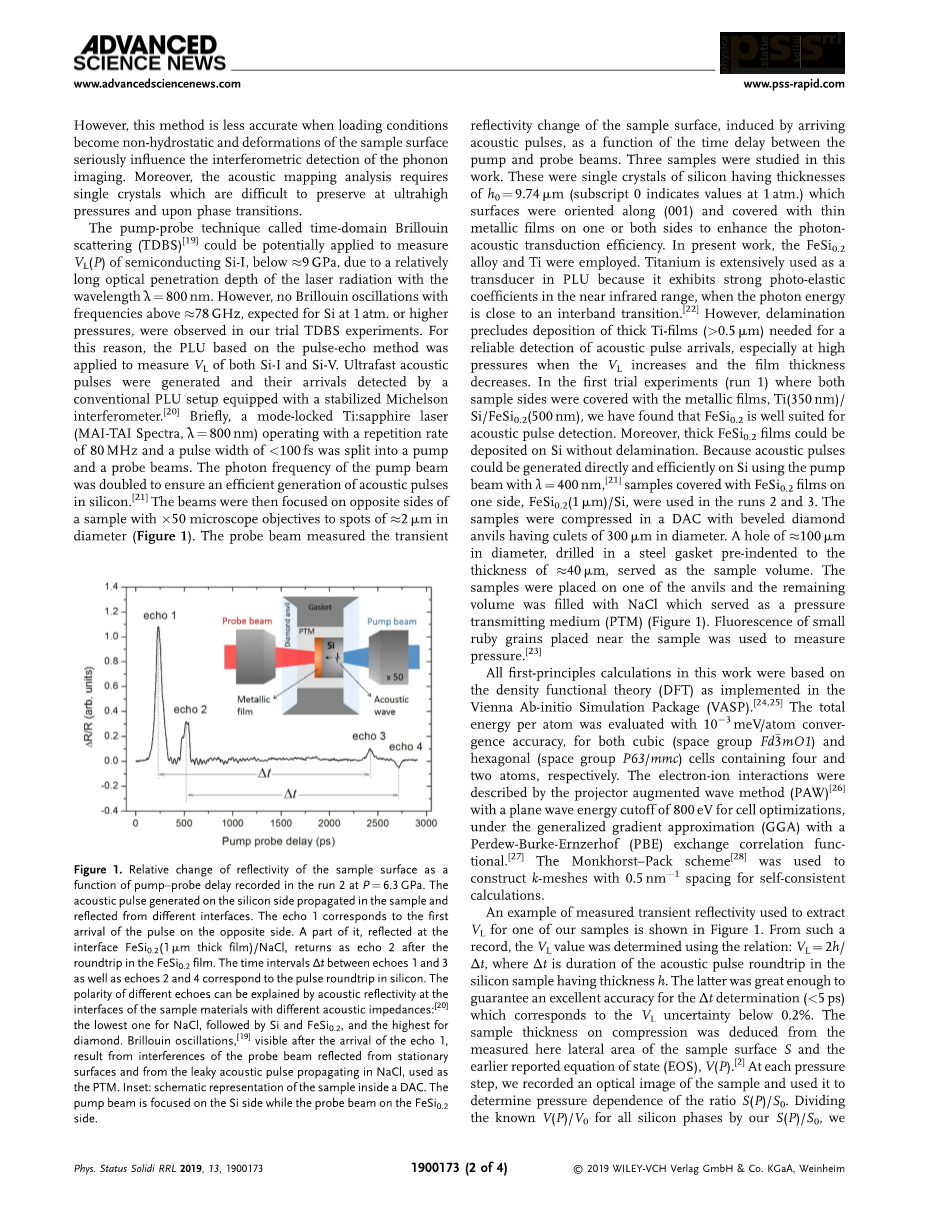
图1:在时实验2中记录的样品表面的反射率随延迟时间的变化曲线。硅侧产生的声脉冲在样品中传播,从不同的界面反射。回波1对应于脉冲在另一侧的第一次到达。一部分在界面()/上反射,在中往返后以回波2的形式返回。回波1和3之间的时间间隔以及回波2和4之间的时间间隔对应脉冲在硅往返。不同回声的极性可以用具有不同声阻抗的样品材料界面处的声反射率来解释::最低,和次之,金刚石最高。回波1到达后可见的布里渊振荡是由固定表面反射的探测光束和作为PTM的中传播的漏声脉冲的干涉造成的。插图:DAC内样品的示意图。泵浦光集中在硅的一侧,而探测光集中在一侧。
由到达的声脉冲引起的样品表面反射率的变化,是泵浦和探测光束之间的延迟时间的函数。在这项工作中研究了三个样品。这些是单身的硅晶体厚度(下标0显示在1 atm下),这些样品的表面取向为(001),被薄金属薄膜覆盖在一个或两个面以提高光声转换效率。在目前的工作中,使用的是和。钛在PLU中被广泛用作传感器,因为当光子能量接近带间跃迁时,钛在近红外范围内表现出很强的光弹性系数。然而,分层阻止了厚的膜的沉积,而这是声脉冲到达的可靠检测所需要的,特别是在高压下,当增加时膜厚度减少。在第一次实验(run 1)中,我们在样品的两边都覆盖了金属薄膜,/ Si /,我们发现非常适合于声脉冲检测。此外,厚的膜可以沉积在Si上而不发生分层。因为如果使用泵浦光,声波脉冲可以直接有效地生成,样本在一边覆盖膜,/Si,用于实验2和实验3。样晶在DAC被压缩在与斜面金刚石砧有300微米直径的底面上。在预缩至40微米厚的钢垫片上钻一个直径为100微米的孔,作为样品室。将样品置于其中一个铁砧上,剩余的体积充入作为压力传递介质(图1)。将小红宝石颗粒置于样品附近的荧光用来测量压力。
在这项工作中,所有第一性的原理计算都基于密度泛函理论(DFT),该理论在仿真包(VASP)中得到了实现。每个原子的总能量按照原子来评估。立方晶系(空间群为)和六方晶系(空间群为)的晶胞分别含4个以及2个原子。电子与离子的相互作用由投影仪增广波法(PAW)描述,该方法的平面波能量截止为800 eV,用于细胞优化,在广义梯度近似(GGA)下具有Perdew-Burke-Ernzerhof (PBE)交换相关函数。Monkhorst-Pack方案用于构建具有的倒格矢自洽计算的间距。
图1显示了一个测量瞬态反射率示例,从中可以得到样品的。的值是根据关系确定的,是声脉冲往返厚度为的硅样品的持续时间。后者足以保证的一个较好的准确性,对应于的不确定性低于。压缩后的试样厚度由试样表面的横向面积和先前的状态方程导出。,在每个压力步骤,我们记录了样品的光学图像,并使用它来确定比例的压力依赖性。我们用已知的所有硅相的除以得到相对厚度变化。对于Si-I相而言,根据早些时候的状态方程:表明,加载条件是静水时,压强在9 GPa以下时样品仍然是一个单晶,在压强为大约9 GPa时接近于向Si-II相的转变。在这一转变之上,和之间的塑性形变相关关系不再成立,这是由于压缩后的非静水状态的增长和硅的高压金属相的低硬度造成的。出于这个原因,时样品的厚度决定使用表达式:,我们记录,因此,10 GPa以上时的不确定性少于,比的不确定性大得多。
所有三次运行的实验值如图2所示。由于Si-II相和Si-XI相与相邻相共存,且文献中还没有很好的建立它们的体积比,进一步分析9-18 Gpa压强范围内的没有意义。压强在9 GPa以下时,只有Si-I相存在,测量的与沿着方向的声速值相对应。我们计算了单晶Si-I相同一方向的声速值,与比较后发现一致(图2)。结合我们的和状态方程,以及质量密度和体积弹性模量,使用众所周知的表达式:和,我们得出了和随压强的变化关系,在图3中,我们将我们的实验值和理论值和与之前进行过的实验和理论的结果进行了比较。尽管我们的GGA值比局部密度近似值(LDA)低10%。但总体上还是达成了良好的一致。
图2:硅的纵波声速与压力的关系图。在左边框和右边框的压力范围内,只有Si-I相(0-9 GPa)和Si-V相(18-38 GPa)存在。在混合相区,Si-I相/Si- II相、Si- II相/Si-XI相和Si-XI相/Si-V相可能共存(见正文)。实验1、2和3的实验数据分别用开放圆、正方形和三角形表示。对于纯Si-I相区域,实验中的不确定性小于预估值。我们基于第一性原理计算的结果用实红线标出:是在Si-I相中沿晶向的声速,和分别是具有简单六方结构的单晶状态下Si-V相中测得的声速的最小值和最大值。对应于沿着c轴方向的声速,是在多晶状态下Si-V相的声速平均值,该值是利用理论值,和Voigt–Reuss–Hill近似得到的。
图3:Si-I相和Si-V相弹性模量的压强依赖性,并给出了相应的Si-I单晶弹性常数。我们的测量值(纯黑色方块)与声子成像法(开放的红色圆圈)和传统超声技术(虚线蓝线)的早期测量值进行了比较。我们将在GGA中的结果(实红线)与在LDA中的早期预测(虚绿线)值进行了比较。高于18 GPa的实心的黑色方块代表这里测量的多晶状态下的Si-V相的,之前测量的用黑色虚线表示。我们的理论值和用实红线表示。
压强在18到38 GPa范围内时,只有Si-V相存在,在压强到达27 GPa之前,我们测量的随着压强增加而缓慢增加。这种依赖关系与我们计算的多晶状态下的随机取向晶粒的Si-V的一致。由以下表达式确定:,各向同性的弹性模量和来自我们使用Voigt-Reuss-Hill近似计算的和得到。这一观察结果表明,在27 GPa之前,Si-V相样品没有出现织构现象。应用逆向方程到我们的实验数据点,结合早期测量的和,对于多晶状态下无织构Si-V相样品,与压强的关系只在27 GPa以下成立(图3)。
从图2中可以看出,压强在27 GPa以上时,我们的实验值随着压强的增加而增加的幅度比在27 GPa以下大得多,并且与理论值有很大的偏差。这表明Si-V相样品在27 GPa以上的压强下出现了显著的织构现象。因为的测量值接近在具有简单六方结构单晶状态下Si-V相样品中测得最大的可能值,我们可以得出结论:随着一些的晶粒数目的增多,发展中的织构现象可以被辨识出来,这些晶粒的c轴沿声脉冲传播方向,并直于砧宝石底面。这一观察结果与之前的XRD工作一致,XRD工作显示在相似的压力下,Si-V相的(001)和(100)峰的强度也发生了很大的变化。我们还在图2中展示了使用我们的得到的混合相位区域的,是根据一个较早的状态方程和方程得到的。在这里,我们假设10 GPa以上的样品只包含Si-II相和以下Si-XI相。这解释了的突然的步进式下降,这种下降在扩展的两相区域中不应该出现。由于缺乏这些资料,这些数据没有得到进一步处理 这里只是为了完整起见而提出。
综上所述,我们从实验和理论上研究了Si-I相和Si-V相的纵波声速和弹性模量随压强的变化关系。在压力作用下,Si-I相的起始单晶发生相变,出现小晶粒随机取向的多晶相。经过三次相变后,Si-V相样品可以看作是弹性各向同性的。对于Si-I相,测量到的与沿着晶向的相对应。对于Si-V相,当且仅当压强在27 GPa以下时,测得的与各向同性多晶状态下的相对应。Si-I相的和随压强的变化关系、使用早期测得的状态方程得到的实验值与之前发表的数据以及我们计算的结果非常一致。更重要的是,我们首次测量了在18- 27 GPa压强范围内多晶状态下Si-V相的和。压强在27 GPa以上时,我们观察到多晶状态下Si-V相样品的织构化,其晶粒优选其c轴沿DAC中的压缩方向。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[236075],资料为PDF文档或Word文档,PDF文档可免费转换为Word


