
英语原文共 5 页
超冷中性原子的合成磁场
Y.-J. Lin, R. L. Compton, K. Jime acute;nez-Garcı a, J. V. Porto1 amp; I. B. Spielman1
中性原子玻色冷凝物和简并费米气体已经被用来以最简单和最基本的形式实现重要的多体现象,而没有许多通常与材料系统有关的复杂现象。然而,这些系统的电荷中立性有一个明显的局限性——一系列有趣的现象是由磁场中带电粒子的洛伦兹力引起的,例如二维电子系统中的分数量子霍尔效应。利用洛伦兹力和科里奥利力的等效性在旋转中性系统中产生合成磁场,可以克服这一限制。这一点可以通过在旋转量子气体(磁场中的超流体或超导体的标志)上的开创性实验中出现的量子化涡流来证明。然而,由于限制最大旋转速度的技术问题、旋转状态的亚稳态性质以及应用稳定旋转光学晶格的困难,旋转方法无法达到量子霍尔物理所需的大范围场。在这里,我们实验性地实现了超冷中性原子的光学合成磁场,这从我们玻色-爱因斯坦凝聚体中旋涡的出现可以明显地看出。我们的方法是利用原子内部状态之间的空间依赖性耦合,产生足以产生大的合成磁场的Berry相,并且不受旋转系统的限制。有了合适的晶格结构,它应该可以达到量子霍尔状态,进行研究拓扑量子计算。
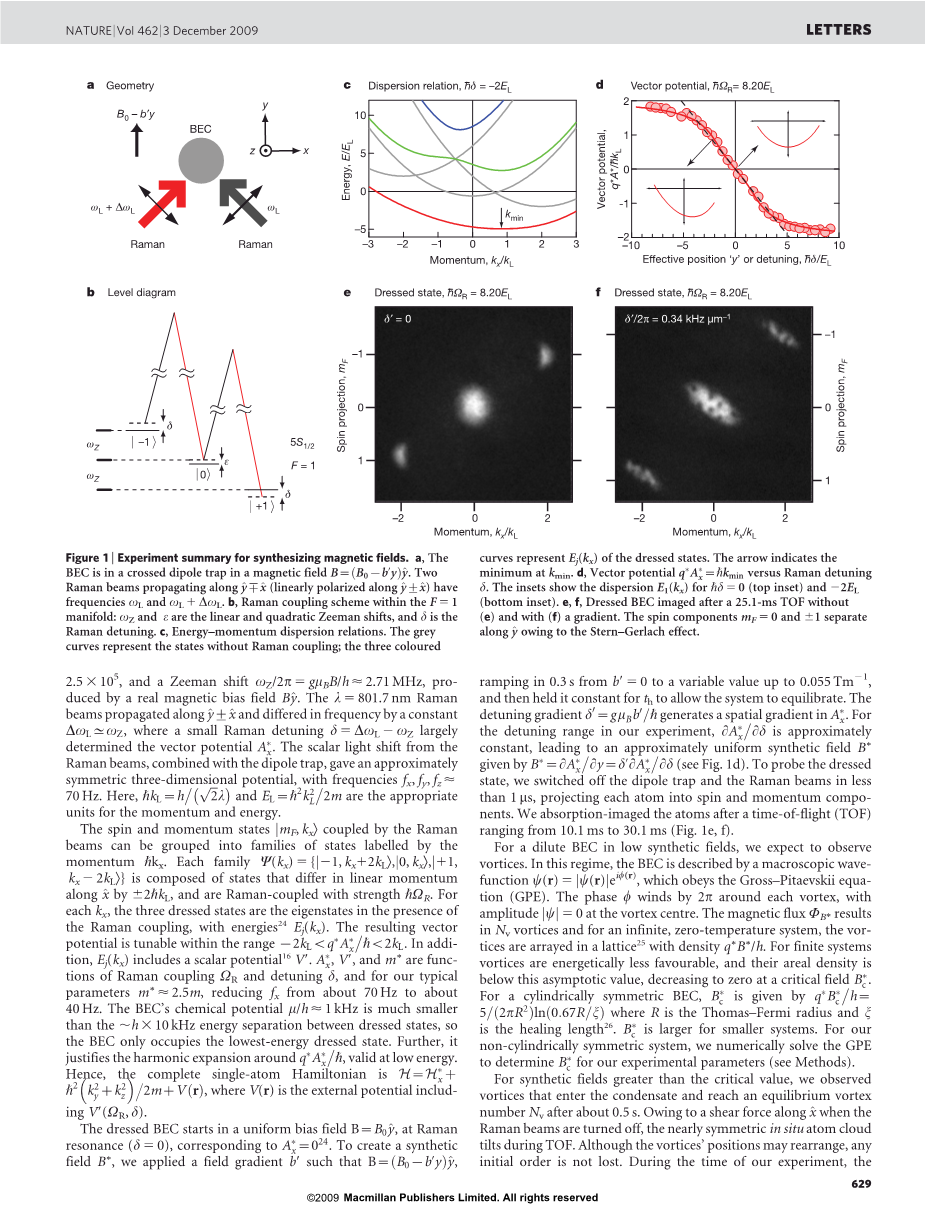
在经典电磁学中,带电粒子q在磁场b中随速度v运动时的洛伦兹力为vtimes;qb,在量子力学的哈密顿公式中,势场起中心作用,单粒子哈密顿量为,其中A是引起场的矢量势,是标准动量,m是质量。在这两种形式中,只有QB和QA是重要的。为了产生中性原子的合成磁场B*,我们设计了一个哈密顿量,它具有空间相关的矢量势a*产生。
量子力学相位是磁场中带电粒子的相关重要量。由于磁场B的存在,带电粒子Q沿闭环运动,获得了相位,其中是封闭磁通量,是磁通量量子。类似的路径相关相位,即berry相位,是由一个缓慢移动的粒子在具有位置相关参数的哈密顿量中沿一条闭合路径进行绝热运动所获得的几何相位。berry相位仅取决于路径上参数的几何结构,与对该相位的动态贡献不同,后者取决于运动的速度。
与Berry相位的密切相关表明,适当设计中性粒子的位置哈密顿量可以模拟磁场对带电粒子的影响。我们通过在耦合不同自旋态的光学场中对超冷原子进行修饰,从而为超冷原子创造了这样一个空间变化的哈密顿量。适当的空间依赖性可以来源于激光束的轮廓,或者像这里一样,源于空间依赖的激光-原子失谐。这种光学方法相对于旋转气体的优势在于合成场在实验室框架内静止存在,使得所有捕获电位都与时间无关。
这种方法所能获得的强合成磁场使研究未探测到的玻色子霍尔态成为可能,该态由填充因子、原子数与磁通量量子数之比标记。量子霍尔物理学中突出的开放性问题集中在基本准粒子激发为任何子的系统上:既不是玻色子,也不是费米子。在某些情况下,这些任意子可能是非交换的,这意味着相互移动它们可以实现量子门,这使得非交换的任意子对这种“拓扑”量子计算非常有趣。在电子系统中,观察到的V=5/2量子霍尔态可能是这样一个系统,但其真实性质仍然不确定。相比之下,具有接触相互作用的v=1玻色子霍尔态具有与电子系统中希望具有的v=5/2态相同的非阿贝尔任意子激发。
为了设计一个矢量势,我们用一对动量差沿x的拉曼激光束照亮了87rb玻色-爱因斯坦凝聚态(BEC)(图1a)。这些激光束将电子基态(图1b)的三个自旋态()耦合在一起,产生了三种修饰态,其能量-动量分散。离子关系)在实验上是可调的。示例分散如图1c所示。其中最小值为kmin的最低值对应于沿 x运动的哈密顿量,即,其中Ax是一个工程矢量势,它依赖于具有合成电荷的原子的外部控制的塞曼位移。m*是沿x的有效质量。产生所需的空间依赖性(见图1d),产生,我们应用了塞曼位移,该位移沿线性变化。结果B*在y=0附近近似均匀,此时(这里,合成洛伦兹力的微观起源是沿X方向的光源,取决于沿Y方向的速度;沿Y方向的力是磁场,取决于X方向的速度。)这样,我们为超冷原子设计了哈密顿量,该超冷原子明确包含一个BEC合成磁场。这与所有现有的实验都有明显的不同,在这些实验中,涡流是由相位旋转或它们的组合产生的。这些早期的研究都提出了一种不同的方法来给产生旋转的系统传递角动量。图1e显示了B*=0原子的实验图像。图1f中的B*gt;0显示了旋涡,这显示了对光学感应合成磁场的观察。
合成磁场实验总结。a,BEC处于磁场的交叉偶极陷阱中。沿(沿线性极化)传播的两个拉曼光束的频率为和。b,在F=1流形内的拉曼耦合方案:和是线性和二次塞曼位移,是拉曼失谐。c是能量-动量扩散关系。灰色曲线表示没有拉曼耦合的状态;三种颜色的曲线表示修饰状态的Ej(kx)。d,矢量电位与拉曼失谐。插图显示了(顶部插图)和(底部插图)的色散E1(kx)。
我们在1064nm的交叉偶极阱中创造了一个87Rb-BEC,加载到原子数n高达2.5*105的最低能量修饰态,以及由真实磁偏场By产生的塞曼位移,拉曼光束沿传播,频率差为常数,其中一个较小的拉曼失谐很大程度上决定了矢量势Ax。拉曼光束的标量光位移与偶极阱相结合,给出了一个近似对称的三维势,频率fx、fy、fzlt;70h。z.在这里,是动力和能量的适当单位。
拉曼光束耦合的自旋态和动量态_可分为由动量标记的一系列状态。每个族都由沿x的线动量差的态组成,并且是拉曼与强度耦合的。对于每个kx,三个修饰态是存在拉曼耦合的本征态,具有能量。由此产生的矢量电位在范围内可调。此外,Ej(kx)包括一个标量势和m*是拉曼耦合和失谐的函数,对于我们的典型参数m*=2.5m,将fx从约70hz降低到约40hz。BEC的化学势远小于,的缀饰态能量分离,因此BEC只占有最低的缀饰态能量。进一步证明了附近的谐波扩展在低能下是有效的,因此完整的单原子哈密顿量是其中v(r)是包括在内的外部势。
图2不同失谐梯度下的旋涡外观。对N=1.43*105原子在保持时间th=0.57s.a–f进行了数据采集,在拉曼耦合下,在25.1 ms的TOF后,修饰态的组分的图像失谐梯度从0到0.43kh/um,涡流数 与的数值在(蓝色圆圈)和8.20El(红色圆圈)处。每个数据点在至少20个实验取平均,不确定度代表一个标准偏差s。在BEC中,插图显示Nv与合成磁通量。虚线表示,根据我们的GPE计算,下面的涡流变得非常不稳定,阴影区域显示了实验参数的1的不确定性。
经修饰的BEC在拉曼共振下开始于均匀偏压场,对应于。为了创建一个合成场B*,我们应用了场梯度Brsquo;,这样 从brsquo;=0以0.3s的速度增加到0.055/TM以下的变量值,并且允许系统进行平衡。失谐半径 。对于我们实验中的失谐范围,近似恒定,导致给出的近似均匀的合成场。为了探测修饰态,我们在不到1毫秒的时间内关闭了偶极阱和拉曼光束,将每个原子投射到自旋和动量分量中。我们在飞行时间(TOF)从10.1毫秒到30.1毫秒(图1e,f)后对原子进行了吸收成像。
对于低合成场中的稀释BEC,我们期望观测到旋涡。在这种情况下,BEC由宏观波函数来描述,该函数遵循Gross-Pitaevskii方程(GPE)。相在每个漩涡周围缠绕2pi,漩涡中心的振幅为。磁通量产生Nv涡,对于无限的零温度系统,涡排列在密度为的格子中。对于有限系统,涡在能量上较低,其面积密度低于此渐近值,在临界场Bc处降至零。对于圆柱对称的BEC,Bc由给出,其中r是托马斯-费米半径,j是愈合长度。对于较小的系统,Bc较大。对于非圆柱对称系统,我们通过数值求解GPE来确定实验参数的B c(见方法)。
对于大于临界值的合成场,我们观察到进入冷凝并在大约0.5s后达到平衡涡数nv的漩涡。由于拉曼光束关闭时沿x方向的剪切力,近对称的位置云在TOF期间倾斜。尽管漩涡的位置可能重新排列,但任何初始位置都会发生变化。在我们的实验过程中,涡流并没有形成格子,并且在不同的实验实现之间,涡流的位置是不可恢复的,这与我们的GPE模拟是一致的。我们测量了两个耦合处失谐梯度的函数(图2)。对于每个,当相应的场超过临界场B c时,涡出现在最小梯度之上。(对于耦合,B*仅在系统上近似均匀,且B*是在BEC区域上的场平均值。)对于绘制的虚拟现实值与,如图显示Nv,涡流区域系统的数值,具有渐近旋涡密度,其中rx(或ry)是沿x或y的托马斯-费米半径。系统大小,因此Bc*,几乎独立于,所以我们期望这个图几乎独立于拉曼耦合。实际上,的数据仅对Nvlt;5有偏差,可能是由于涡流成核的复杂动力学。
图3显示了一系列图像,这些图像显示漩涡在系统边缘成核,完全进入平衡密度,然后随原子数衰减。漩涡成核的时间尺度弱依赖于B*,而对于更大的B*和更多的漩涡则更快。涡流数约为0.3s,而约为0.5s。对于(B*趋近于B c),单个涡流始终保持在BEC边缘附近。在缀饰态下,拉曼光束的自发辐射将原子从陷阱中移除,导致粒子群随1.4(2)-s寿命衰减,平衡涡数随BEC面积的增大而减小。 .
为了验证经过修饰的BEC已经达到平衡,我们以两种不同的方式准备了相同的系统。首先,我们改变初始原子数,并在50.57s的固定保持时间内测量Nv作为原子数n的函数。第二,从一个大的原子数开始,我们测量了Nv和N,因为它们随th的减小而减小(图3)。图4比较了两种方法测得的Nv与N,每种方法对应于的两个失谐梯度。数据表明,对于这些制备方法,Nv作为N的函数是相同的,提供了证据,证明对于,nv已达到平衡。随着原子数n的减少,当临界场随n的减小而增大时,最后一个涡将离开系统。
总之,我们已经证明了中性原子的光学合成磁场是由Berry相产生的,这是物理学中的一个基本概念。这种新方法不同于旋转气体实验,在旋转气体实验中,很难添加光学晶格,并且旋转受到加热、亚稳态和添加大角动量的困难的限制,从而阻止进入量子霍尔机制。在我们的方法中,一个突出的特点是容易添加光学晶格。例如,二维晶格的加入使得研究霍夫施塔特蝴蝶的分形能级成为可能。此外,一维晶格可以将BEC划分为垂直于场的二维系统阵列。合适的晶格结构允许进入当时量子霍尔机制的系统,每个系统包含一组约200个原子的二维系统,以及大约的逆相互作用能量。
图3漩涡形成。a–f,30.1 ms TOF后,在0.019 s至2.2 s之间保持时间th后,_分量的图像。失谐梯度在耦合处倾斜至0.31khz/um。g,上面板显示了D0的时间序列。(A.U,任意单位。)底部面板显示涡流数Nv(固体符号)和原子数N(开放符号)与th,总体寿命为1.4(2)s。括号中的数字是统计和系统1s不确定性的不相关组合。
我们在交叉偶极阱中创建了87Rb BEC,在中的个原子。对于,二次塞曼位移为,其中g是朗德因子。为了保持在BEC的中心,当我们在场梯度brsquo;,我们改变高达7El。同时,我们减少了20%的偶极子束功率,产生了沿着X的大约40赫兹的陷波频率。此外,失谐梯度dy使标量势v9沿^yy抗俘获,使fy从70Hz降低到最大的d0的50Hz。拉曼光束的自发辐射使Th50的原子数减少到,而凝聚分数为0.85。数值方法。我们将我们的数据与有限温度二维随机GPE模拟进行了比较,其中包括通过失谐梯度依赖于y的修饰态色散E(kx,y)。我们发展了与时间相关的预测GPE:
p投影到一组显著占用的模式上,g2d参数化二维交互强度。随机GPE模型的相互作用的高度占用模式所描述的Y和稀疏占用的散热模式和相关的噪声项。我们通过使g2d依赖于局部二维密度,近似地解释了沿z的有限范围。对于低温,该二维模型正确地恢复了三维托马斯-费米半径,并给出了预期的二维密度分布。这些定量的细节需要正确计算进入系统的第一个漩涡的临界场或临界数,这些漩涡直接与二维冷凝区域相连。
参考文献
1. Greiner, M., Mandel, O., Esslinger, T., Hauml;nsch, T. W. amp; Bloch, I. Quantum phase
transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature
415, 39–44 (2003).
2. Regal, C. A., Greiner, M. amp; Jin, D. S. Observation of resonance condensation of
fermionic atom pairs. Phys. Rev. Lett. 92, 040403 (2004).
3. Zwierlein, M. W. et al. Condensation of pairs of fermionic atoms near a Feshbach
resonance. Phys. Rev. Lett. 92, 120403 (2004).
4. Tsui, D. C., Stormer, H. L. amp; Gossard, A. C. Two-dimensional magnetotransport in
the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
5. Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid
with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).
6. Zwierlein, M. W., Abo-Shaeer, J. R., Schirotzek, A., Schunck, C. H. amp; Ketterle, W.
Vortices
资料编号:[5368]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


