英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
用于设计渐进多焦镜片的变分差数值方法
魏江,魏竹宝,唐庆林,王汉泉
摘 要:我们提出了一种变差方法来设计渐进镜片(PAL)的光学自由曲面。PAL的前表面带有三个重要区域,包括远视,近视和中间区域,通常用于通过逐步平滑地分配三个区域的光焦度来矫正老花眼。设计PAL的问题可以看作是功能最小化的问题。与现有的用B样条有限元方法解决问题的文献相比,提出的变分数值方法的实质在于直接通过有限差分法和数值正交函数最小化泛函,而不是逼近方程的解。对应于函数的Euler-Lagrange方程。光学工程师很容易理解和实施它,数值结果表明它可以在几秒钟内为光学工程师提供令人满意的设计。我们相信,人们的方法可以成为设计各种规格PAL的强大候选工具。
关键词:渐进镜片;变差法;线性化;背景表面;功能最小化问题
当人们40岁时,自然的衰老过程开始影响人们的视力,并且人们的眼睛晶状体变粗并逐渐失去其柔韧性,以至于人们无法专注于近点。这会导致老花眼。因此,老花眼的人自然需要戴眼镜来矫正视力。人们通常可以使用单光镜片来纠正此问题。但是,尽管这些可以为附近地区带来很好的视野,但人们仍需要摘掉镜片,以便对远距离区域有良好的视野。为了避免这种不便,已经设计了更复杂的镜片,例如双焦点镜片,三焦点镜片和渐进屈光镜片(PAL)。
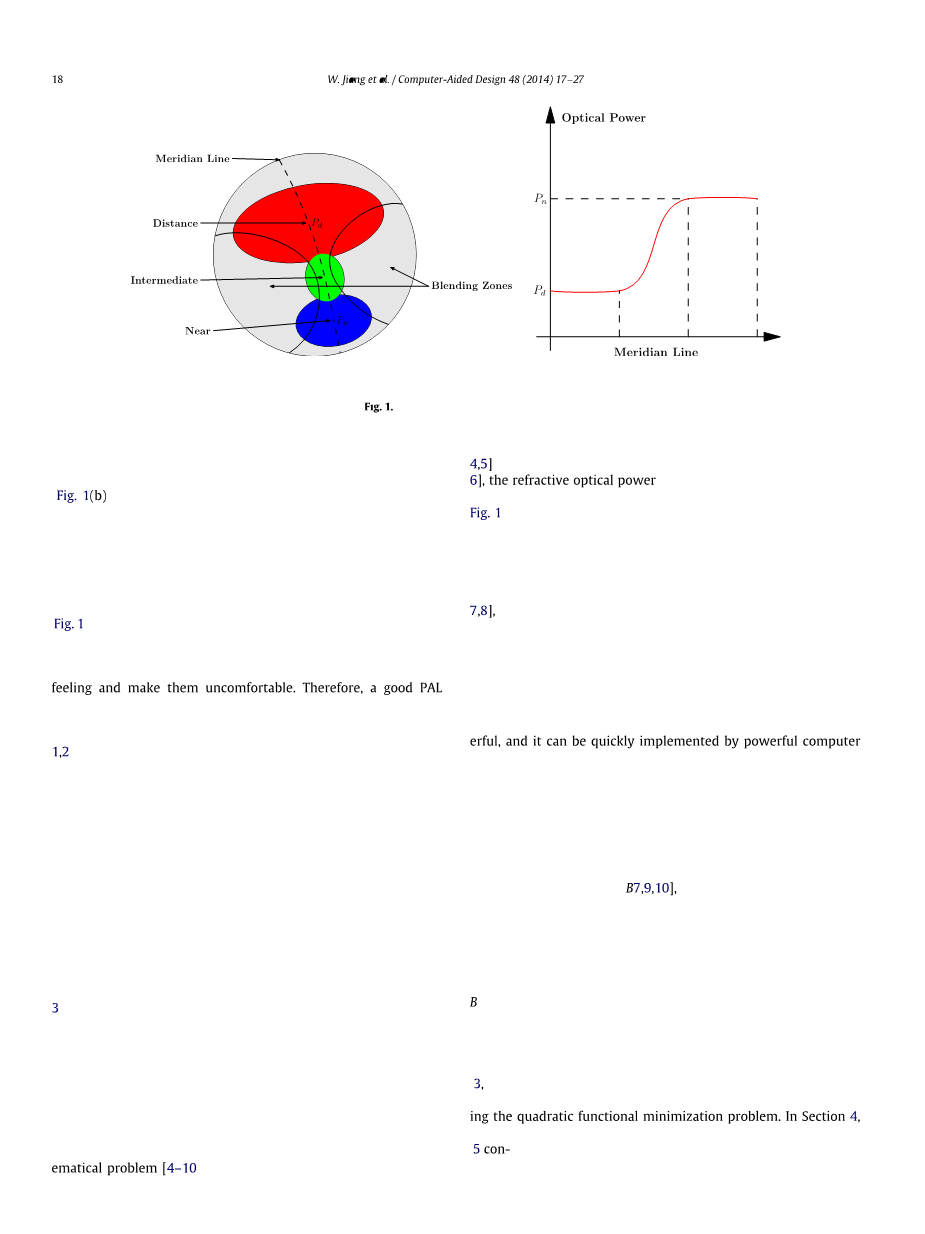
双焦点镜片是本杰明·富兰克林于1784年首次发明的,因为当时他视力不好,它可以分为两部分,上半部分用于远距离观看,下半部分用于阅读。三焦点镜片由三部分组成,另外还有一部分用于在中间区域观看。这两类镜片的主要缺点是,当眼睛从远距离物体移到近距离物体时,视力会跳动。PAL,也称为无焦点双焦点镜片,可以消除视力跳跃的缺点。图1 显示了PAL的示意图。如图1 所示(a),PAL的前表面具有三个不同的视区,包括远视区(即远视区),近视区和中间区。更准确地说,PAL在上部具有较大的远视区域,在下部具有低折射光焦度,而在较小的近视区域具有在下部的高折射光焦度,而中视区域的光焦度则逐渐变化,并且Smooth用于连接PAL的上部和下部。图1(b)显示了沿子午线在PAL的三个不同视区上折射光焦度的典型分布。通常,良好的PAL设计要求根据每个患者的处方逐渐且平稳地改变远视,近视和中间区域的光焦度,并且三个区域上的像散必须同时减小。但是,其余部分称为图1 所示的混合区域(a),由于沿三个区域的规定功率分布,也不可避免地具有散光。尽管混合区是眼镜佩戴者最不经常使用的区域,但散光会给他们带来不良的视觉感觉并使他们不舒服。因此,良好的PAL设计还需要要求混合区具有较低的像散。
早在1907年,英国验光师欧文鸟纲制成的原型设计的PAL[1][2]。他的设计思想来自大象的躯干形状,它由一个圆锥形的后表面和一个带有相对轴线的圆柱形前部组成,以产生动力级数。该设计是现代PAL的原型,但当时尚未商业化。自从第一个现代设计的发明和1960年代左右进入市场以来,PAL因其消除了镜头的远视和近视部分之间的视线跳线的能力而逐渐为全球客户所接受,并提供眼镜配戴者在不同视区之间可以平稳过渡。如今,PAL作为用于矫正老花眼的高性能眼镜镜片已经获得了世界范围的认可,目前占所有多焦点眼镜销售额的一半以上[3]。由于眼镜配戴者的视觉要求因人而异,因此一段时间以来,人们已经了解到传统的“千篇一律”渐进式镜片设计框架不再适合每个渐进式配镜者。因此,设计人员需要通过考虑各个渐进镜片佩戴者的独特视觉要求来定制更合适,更专业的眼镜片。因此,设计方法的进步对于设计下一代PAL变得越来越重要。
设计PAL通常被认为是一个非常复杂的数学问题。通常,设计方法可以分为两类,直接方法和间接方法。在直接的方法,例如Winthrop[4][5]和Baudart、Ahsbahs和Miege[6]的研究工作中,折射光焦度首先沿着一个称为子午线,然后通过规定垂直于子午线的曲线,从子午线产生透镜的表面。选择这些曲线的形状以在子午线上具有所需的表面曲率。但是,这种设计方法的性能通常不能令人满意,因为不能有效控制散光的分布。对于间接方法,例如Loos等人提出透镜设计可以简化为优化问题或功能最小化问题[7][8]。在这种方法中,将设计并预先给出成本函数,该函数试图在折光力的期望分布与不希望的像散之间取得平衡。设计目标是通过数值方法使成本函数(功能性)最小化。间接方法通常更有效,更强大,并且可以通过强大的计算机仿真快速实现。它还可以提供更精确的控制,以控制镜片表面的光焦度和像散分布。因此,它代表了设计定制PAL的强大候选工具。
在本文中,我们集中于设计PAL的间接方法。基于功能最小化数学模型,我们提出了一种有效的变分数值方法来解决该问题。与其中由解决的问题现有的文献相比较B样条有限元法[7][9][10],所提出的变差数值方法谎言在由有限差分法直接最小化的功能,而不是在近似本质相应的Euler–Lagrange方程对函数的解。光学工程师很容易理解和实现它,并且其内存和计算成本比B样条有限元方法。我们的数值结果表明,它可以在几秒钟内为光学工程师带来令人满意的设计结果。
1 数学模型
1.1 函数最小化问题
对于PAL的设计,根据每个患者的处方,光功率是光学工程师的两个关键设计参数之一。通常,PAL的光功率是由前表面和后表面的形状以及透镜的材料特性决定。在透镜非常薄的假设下,我们通过设置d = 0 从(1.1)得到一个近似公式:
(1.2)
对于本文讨论的PAL,将背面选择为具有恒定平均曲率的球形表面。因此,根据公式(1.2),通过平滑且逐渐地改变前表面的平均曲率,可以实现PAL 的光焦度P的渐进式变化。在本文中,设计目标是确定PAL前表面的形状。为简便起见,光焦度P称为纸张其余部分中前表面的光焦度。光焦度以屈光度为单位,其定义为焦距(即平均曲率)乘以(n - 1)的倒数。因此,屈光度为单位1 /米。
PAL的另一个关键设计参数称为(表面)像散或圆柱。假定kappa; 1 和kappa; 2 是前表面的两个局部主曲率,则透镜的像散被定义为
(1.3)
并且像散的单位也用作屈光度。我们可以看到,PAL设计中感兴趣的两个参数,光功率和像散分别仅与两个主曲率的和和差有关。通常,需要光功率为患者提供适当的矫正,而散光对于纸上的PAL设计是不利的影响。因为如果镜片具有严重的散光,除非佩戴者的眼睛有任何散光缺陷,否则会发生视力畸变并且使配镜者感到不适。
理想的PAL是指具有规定的平滑渐进光焦度分布并且在镜片上各处零散光的PAL。但是,为了使整个表面的像散为零,该表面必须是不能提供规定的渐进屈光力的平面或球面。因此,达到所需的光功率分布和不希望的像散的两个关键设计因素相互竞争。根据上述观察,Loos等提出了一种确定薄渐进镜片形状的方法,该方法使设计人员能够创建各种不同的设计。根据他们的方法,要设计PAL的表面,我们可以最小化以下功能[7]:
(1.4)
其中Ω sub; R2是一个有界区域,u := u(x, y) 限定了设计的透镜表面的形状,kappa;1 := kappa;1(x, y) 和 kappa;2 := kappa;2(x, y)分别代表曲面的两个主曲率,dA代表u(x, y)图上的面积元素和三个功能alpha; := alpha;(x, y),beta; := beta;(x, y) and P0 := P0(x, y) 被预先规定的函数Omega;。更准确地来说,所规定函数P 0是期望的光功率分布,并且其大小从远视区域到近视区域连续增加;权重函数alpha; 和beta; 控制散光的发生与从规定的功率分布函数P 0导出的比率之间的比率关系。
将定义的平均曲率H和高斯曲率K替换为
(1.5)
到功能(1.4)中,我们可以将设计PAL的问题表达为以下最小化问题:
(1.6)
假设在透镜的表面是由图形函数给出的笛卡儿坐标z = u(x, y) for (x, y) isin; Ω,则平均曲率H和高斯曲率K可由下式给出
(1.7)
面积元素d A可以表示为
(1.8)
将(1.7)和(1.8)插入(1.6)中,我们获得了设计PAL镜头的功能最小化问题。
关于(1.6)中的泛函的Euler-Lagrange方程是一个高度非线性和高阶偏微分方程。因此,通常很难通过直接数值计算来解决问题(P)。在文献中,王等[9][11][12]通过从变分问题产生的欧拉-拉格朗日方程的线性近似方法(P)设计PAL。通过假定设计的透镜表面是两个部分的组合(一个是指定的球面背景表面,另一个是相对于所选球面的小摄动表面),他们简化了关于功能的Euler-Lagrange方程。(1.6)为线性四阶偏微分方程。在包括边界条件,部分边界条件和自然边界条件的各种边界条件下,它们针对线性四阶偏微分方程[ 11 ]都显示了解的存在性和唯一性以及正则性。此外,通过使用B样条有限元方法,他们设计了一种求解线性化问题的数值算法[ 9 ]。
1.2 背景表面的线性化
按照Wang等人[9][11]提出的线性化方法。用于设计的PAL,我们假设表面函数u(x, y)可分为两个部分:
(1.9)
其中w := w(x, y) 是选定的背景表面,而 v := v(x, y) 表示扰动表面。因此,关于 u(x, y)的函数最小化问题(P) 可以转换成关于小扰动函数v(x, y)的问题。将(1.9)替换为(1.7)和(1.8)并且进一步假设扰动函数v(x, y)满足:|nabla;v| asymp; 0和|nabla;2v| 从上方域中界Omega;,我们可以得到用于近似表达式H,K 和g 作为
(1.10)
(1.11)
.
插入(1.10)和(1.11)到(1.6) ,我们得到以下功能这是一个近似 J(u)在(1.6) :
(1.12)
对于任何给定的背景表面 w(x, y),将(1.10)和(1.11)代入(1.12),我们可以轻松地发现函数I(v;w)仅取决于扰动的二阶偏导数函数 v(x, y),即项v xx,v xy,v yy,它们都是平方形式。应该注意的是,为简单起见,我们可以删除表达式(1.12)中的所有常数项,并且仍将函数表示为 I(v;w),则可以用以下二次函数形式表示函数 I(v;w) :
(1.13)
其中Omega; 对所有自变量 x, y,vxx,vxy,vyy,被乘数 F (x, y,vxx,vxy,vyy) 是连续的,可以定义为
(1.14)
其中系数一个ai, i =1, 2,...,9由下式给出
在文献[9][11][12]和在本文中,为简单起见,背景表面通常选择为球形,即
(1.15)
其中R是要确定的常数。在w的球面背景下,注意(1.7),我们得到
我们在此指出,也可以使用其他类型的背景表面,但为简洁起见,在此省略其调查和讨论。
由于所使用的镜片通常圆形的,在实践中,用于设计PAL透镜,计算域 Omega; 通常选择为包含圆形结构域的较大的正方形。当一个人最终完成设计时,可以忽略另一个零件,而将目标圆形零件保留为制造原型。因此,在我们的理论设计中,我们总是选择计算域,以L 作为平方的长度。
由于带有(1.14)的泛函(1.13)是典型的二次泛函,并且它仅取决于扰动函数v(x, y)的二阶偏导数,因此,如果函数v0(x, y)最小化函数I(v;w),那么很容易检查函数 v0(x, y) I(x, y)也最小化函数 I(v;w),前提是I(x, y)是域Omega;上的线性函数,即 I(x, y) = c1x c2y c3,其中c 1 ,c 2和c 3为任意三个给定的常数。为了确保最小化器对于最小化问题的唯一性,我们可以固定扰动面的值v(x, y)在域Omega;的三个点(例如三个角)处。因此,为了设计PAL的表面,我们需要针对扰动表面函数 v := v(x, y)解决以下线性化函数最小化问题:
(1.16)
其中背景表面w 被选为球面(1.15)。
2 数值算法
在本节中,我们将提出一种变分差分数值方法,该方法通过使用梯形积分规则逼近积分和通过有限差分逼近导数来解决线性化函数最小化问题(LP)。
表示网格尺寸h =△x = △y
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[410197],资料为PDF文档或Word文档,PDF文档可免费转换为Word


