
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
可调谐四阱铁电范德华耳晶体
作为快速增长的二维和准二维电子材料族的电势控制电介质,层状硫代磷酸盐和硒化磷酸盐已引起关注。在这里,我们报告了密度泛函理论计算,量子分子动力学模拟以及可变温度,压力和偏置压电响应力显微镜数据的组合,以预测和验证不寻常的铁电特性的存在——用于位移的单轴四势阱- 的间隙引起的。计算得出的位移势能图受应变的影响很大,这说明了负压电系数的由来,使成为单轴多阱铁电体的一个罕见例子。实验数据验证了四个极化状态的共存,并探索了温度,压力和偏置相关的压电和铁电特性,这些特性得到了偏置相关的分子动力学模拟的支持。这些现象为基础研究以及在数据存储和电子领域的应用提供了新的机会。
近年来,层状硫代磷酸盐和硒化磷酸盐家族作为快速增长的2D和准2D电子家族的潜在控制电介质而受到关注。稳定在硫代磷酸盐中的金属离子的相对较低的氧化态导致了所需的特性,包括磁,偶极和相关电子有序化,为功能异质结构提供了新的机会,电场可调界面和具有中等光学带隙的层状材料。特别是,这些材料通过剥落为超薄铁性体结构开辟了一条直接途径,同时避免了3D粘结材料中不可避免的悬空键。它们使电子能够与2D材料,例如石墨烯和过渡金属硫族化合物(TMDs)向超越摩尔的电子设备,包括隧道结和铁电体电场效应晶体管,进行电场可调接口。此外,它们还具有很大的离子电导,可能导致无法探索的耦合现象,例如铁离子态。所有这些观点共有的一个基本问题是间隙结构在电子和磁有序状态的形成中的作用,以及间隙是否提供了控制这些行为的新方法,是对传统刚性晶格材料的补充甚至是无法实现的。
块状,特别是亚铁电的,其中和原子在每一层中沿相反方向位移。为简化起见,我们将称为铁电体。尽管接近室温的极化值约为3.5 ,最近发现具有负的纵向压电系数。负纵向压电系数很少见。已知只有另一种材料聚偏氟乙烯具有这种特性。六角ABC铁电体的理论研究,其他纤锌矿和闪锌矿化合物和定向域壁的孪晶铁电钙钛矿已经预言了这种效果,但尚未通过实验实现。在T gt; ~42 °C时,铜原子非常易移动,可以同时占据层内和层间位置,从而导致无序状态。You等人在最近的一篇论文里证实了这一发现。他描述了两个具有不同极化值的不同相位。没有研究第二个高极化相的压电或铁电性能。
在这里,我们报告发现了由中的间隙引起的一种不寻常的铁电特性,即用于位移的单轴四势阱。我们在理论上和实验上证明了这种不寻常特性对诸如极化和压电之类的基本特性的影响。我们首先报告基于的总能量计算,作为连续位移的函数,揭示了沿z轴在每个极化方向上存在两个能量最小值。四阱结构由分层结构直接启用,这导致间隙内的第二个稳定位置,并且它们之间只有很小的能垒。利用四阱势的演变以及系统中的机械应力作为施加应变的函数,可以推论出两个极性相各自的纵向压电常数。使用空间分辨的可变温度压电式力显微镜测量来证明两个相的逐渐相互转换接近居里温度。最后,我们在实验和理论中报告了通过局部施加的电场在极化状态之间转换的能力。总体而言,这些发现确立了在这种以及其他可能的分层固体中跨越间隙的化学相互作用的重要性。他们进一步指出了确定性途径,通过该途径可以增加这种材料家族中的自发极化。
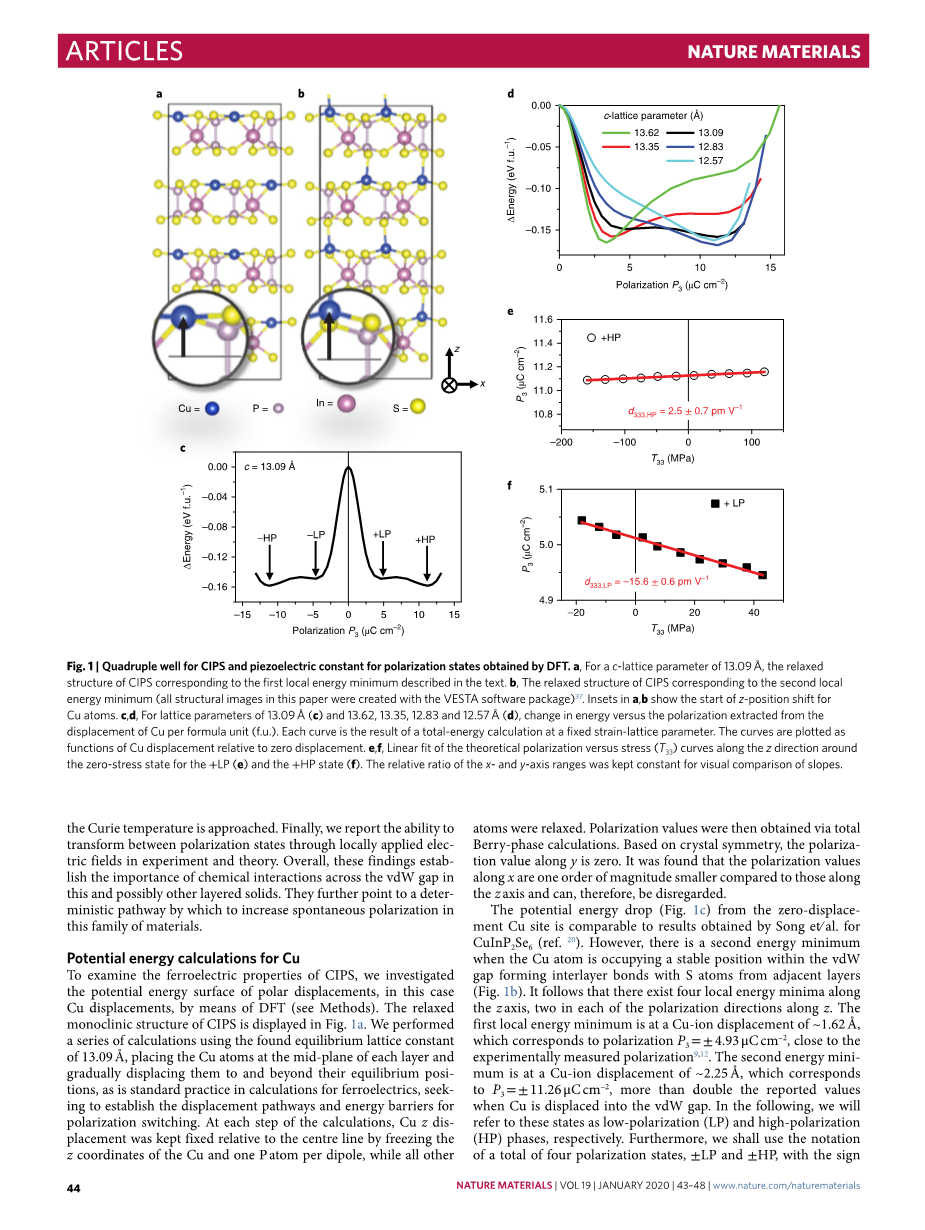
图1 CiPS的|四重阱和DFT得到的极化状态的压电常数。a,对于13.09 a的c晶格参数,文中描述的第一个局部能量最小值对应的CIPS的松弛结构。b、第二局部能量最小值对应的CIPS的松弛结构(本文所有结构图像均使用VESTA软件包创建)37。在a、b中插入量表示Cu原子z位置移动的开始。对于13.09 A (c)、13.62 A (d)、13.35 A (d)、12.83 A (d)和12.57 A (d)的晶格参数,能量随公式单位(f.u)中Cu的位移的极化变化。每条曲线都是在固定应变格参数下计算总能量的结果。这些曲线被绘制成铜位移相对于零位移的函数。e,f,理论极化与应力(T33)在零应力状态( LP (e)和 HP (f)状态)z方向上的线性拟合。
铜的势能计算
为了检查的铁电性能,我们通过研究了极性位移的势能面。图1是的松弛单斜结构。我们使用平面晶格常数进行了一系列计算,将铜原子放置在每一层的中平面,并逐渐将其移动到平衡位置及超出其平衡位置,这是铁电学计算的标准做法,建立极化转换的位移路径和能垒。在计算的每个步骤中,通过冻结的z坐标和每个偶极子一个P原子,使z位移相对于中心线保持固定,而所有其他原子放松。然后通过总的贝里相位计算获得极化值。基于晶体对称性,沿y的偏振值为零。已经发现,沿x的极化值比沿z轴的极化值小一个数量级,因此可以忽略。
势能下降(图1c)从零位移位置点得到的结果与Song等人用于获得的结果相当。但是当原子在间隙中占据稳定位置并与来自相邻层的S原子形成层间键合时,存在第二个能量最小值(图1b)。因此,沿着z轴存在四个局部能量最小值,沿着z的每个偏振方向中存在两个局部能量最小值。第一个局部能量最小值处于的铜离子位移处,对应于极化,接近于实验测量的极化。第二个能量最小值为铜离子位移,对应于,是将位移到间隙时报告值的两倍以上。在下文中,我们将使用总共四个极化状态的符号,即和,并带有符号,指示它们相对于z轴平行或反平行的方向。基于Stengel和因格斯,我们将描述为具有随c轴的位移或极化值而变化的四阱电势曲线的铁电材料,或简称为四阱铁电体,反映了这一含义。
我们注意到,总能量曲线如图1c 所示,是在固定的c晶格参数(固定的体积),相的平衡值下计算出来的,从而随着c参数的松弛,状态的能量将降低。确实,如补充图1a所示,相的松弛结构的平衡c晶格参数为。我们确认了即使在弛豫晶格参数下,位移的四势阱也存在(补充图2)。
与具有可通过电场访问的具有不同极化轴的独立双阱铁电相的材料(例如)不同,由于和相的单轴极化矢量以及总能曲线的强烈重叠,因此无法将这两个相分别描述为正常的双阱电势铁电相。特别地,和状态之间的位移路径包含 相的稳定位置,这在势能曲线中产生了额外的局部最小值。因此,四阱铁电术语比 将描述为具有两个不同铁电相的材料,每种材料都具有双阱电势,更为准确。
压电性能的预测
根据以上结果,我们在不同的 c 晶格参数下,根据位移进行了总能量计算。我们将 c 参数更改了相应的数量,将其他晶格参数保持不变,并允许原子移动。根据其他层状材料 的介于0.1 和 0.3 之间泊松比估算,我们发现微不足道的结构,能量和极化变化。已经发现,大多数压缩本身表现为间隙的减小,而层厚度仅略有变化。从这些结构,我们计算出能量曲线,离子-离子距离,极化和机械应力。
可以看出,对于较小的c晶格参数,状态的局部能量最小值消失,而对于较大的c晶格参数,状态的局部能量最小值消失,见图1d(另请参见补充图3a,b),出于对称原因,该图仅显示了正极化状态。该结果表明,四重阱可通过应变调节,并且可以变成双重阱。结果,极化值也取决于c晶格参数(补充图3c,d)。因此,该理论的关键预测是以下事实:尽管在相和相之间的能垒小于热能,但在室温下,两相的(玻耳兹曼常数乘以温度)可以通过改变 c 晶格参数来稳定。
在图1e,f,我们显示了两相在其各自的平衡晶格常数附近的正极化态的极化强度与应力的关系,其特征是零应力。从这些数据中,我们可以如下提取纵向压电系数。
可以通过位移场矢量定义第三极压电张量,其中是电场矢量, 是极化矢量,而是真空介电常数:
(1)
其中是第二级应力张量。因此,线性拟合到图1e中的计算点,可用于获取两个正极化态的纵向压电系数。我们发现,在平衡 c 晶格参数值附近,状态具有较大的负压电系数,,而状态具有相对较小的正压电系数常数。状态的压电系数的负号与以前的工作一致,其中发现负压电系数的证据。这项研究报道了高极化态的压电和铁电性质。
在状态下,压电响应的负号的原子起源可以追溯到四阱电势中作为位移函数的高度非谐性,这是潜在的最小应变响应的基础。特别地,我们发现晶格沿着层间堆叠方向的压缩导致远离位置的位移增加。结果,自发极化随压力而增加,如图1e所示。对于较小的负应力,会产生净的负纵向压电响应。相反,状态表现为常规方式,在晶格压缩下表现出降低的位移,如图1f所示,因此为正压电响应。然而,第二最小值( 状态)的应变相关性相对较小,导致压电常数较小。我们可以将此结果归因于这样一 个事实,即正应变会削弱整个间隙中的相互作用(较长的键长),这将导致较低的极化,而增大的距离将导致更大的极化时刻和更高的极化。净效应是这种高极化方案的极化强度接近恒定。
压电常数的实验验证
在下文中,我们提供了使用PFM证明所有四种极化状态均存在的直接证据,如方法中所述,压电常数可以通过应变的变化表示为电场的函数(等式(2))。PFM测量动态表面位移与通常沿着表面法线(平面外)施加的电压。从PFM信号中提取压电张量分量非常复杂,因为它只能探测表面位移但3D体积没有变化,并且信号可以受应变,偏置尖端周围的径向场分布或机械夹持器的影响。PFM通常被称为探测有效纵向压电常数,通过 得出。已经表明,在某些系统中,这是沿着探测的结晶轴与压电张量组件紧密对准:
(2)
在这里,PFM探测有效纵向压电常数 d,它与最紧密对准,因为探测到的表面位移和施加电场的主要分量与的 z 方向对准。
我们在室温和 70°C 之间的相分离,和() 相上进行了PFM实验。是无铜且非铁电的,它使我们能够考虑非铁电信号对压电响应的局部测量的影响。屏蔽程序完成后,分别分析了来自和的PFM响应(补充图4)。
图2由PFM实验量化的|压电常数。a、用PFM在室温下测量的定量压电常数图。色标描述了测得的压电传感器的大小和方向。b,高斯函数下CIPS相位测量值的直方图符合四个不同的最大值。虚线描绘了四种极化状态的理论预测值。
室温下的PFM图像(图2a)表现出铁电的强烈压电响应和非铁电相的接近零信号。此外,相位的压电响应直方图(图2b)显示了四个截然不同的最大值,它们与理论上的预测值非常吻合,并由高斯函数(红色区域)描述。峰的位置代表平均值,而宽度对应于误差线。提供的有关和相的压电常数的符号和大小的信息用于将所有四个偏振态唯一地分配给观察到的PFM对比度水平。我们确定一对数值和,分别对应于相的正极化和负极化状态,理论值为。和 这对数值被分别分配给相的负和正极化状态,这与的理论绝对值极为一致。由于和相之间的能量垒非常小,低于室温下的热能,因此只能通过局部应变稳定来解释PFM对空间分离的和相的观察,也就是c晶格参数的局部变化,这证实了我们基于图1d的理论预测。假定局部应变分布取决于样品历史和合成条件以及缺陷的数量。因此,估计使用 Maxwell–Boltzmann 分布的和相之比不合适。
图3采用PFM测量的|温度相关极化状态分布。,与温度有关的烤瓷测量室温至70°C在居里温度从10times;10mu;m2区域选择(补充图。5)。b,只测量了压电响应分析了CIPS的直方图。c,温度相关的压电常数提取为四种不同的状态,与理论压电常数进行比较。数据点是每个相位的直方图峰值的位置,误差条对应的是峰值宽度。
温度引起的极化状态之间的跃迁
相应地分配了观察到的极化状态后,我们现在可以使用依赖于温度的PFM测量,在局部尺度上观察所有极化状态向居里温度的演化。(图3a和补充图5)。根据图像的统计分析(图3b),我们得出了四个极化态 d 值的温度依赖性,并绘制了它们的轨迹(图3c)。相位用作参考,并且随温度变化很小,从而确认不存在非压电信号源(另见补充图6a)。从室温到 55°C,所有四个极化状态都存在。在 60°C 时,随着状态消失,极化状态的数量减少到三个。在居里温度以上无法将的压电常数与区别开来之前,将温度进一步升高至 65°C 可以将极化态数减少到一个。状态的相互转换阻止了高极化状态的居里 温度的直接测量,但是本身的相互转换在应用程序的上下文中可能是有用的,例如,在利用热电或电热响应中。正如所预测的那样,铁电特性对应变非常敏感,从在不同机械压力下获得的PFM图像可以明显看出(参见扩展数据图1和补充图7)。
图4 |偏极化开关。,地图的压电常数3times;3mu;m2区域,与感兴趣的领域突出显示。b、铁电CIPS相中CIPS 1和CIPS 2两畴中,在3times;3点栅极上,压电滞环作为直流偏置Vdc的函数,由PFM测量。数据点为响应的均值,误差条对应于通过量子分子动力学模拟得到的可逆Cu位移。在四层CIPS样品的两个中间层中,四个铜原子最初在负电场作用下发生位移,并在250ps时转变为正电场。顶层和底层的铜原子分别被染成蓝色和红色。CIPS的结构是参照Cu的位置来显示的。
极化态之间的场致跃迁
最后,我们使用转换光谱论证了电场下的偏振开关。为了进行实验研究,我们根据压电常数图选择了两个区域(图4a),并在较大的负数中执行 3times;3 点网格,正压电常数( 1,)和小的正压电常数( 2,)区域,如图4a所示。两个截然不同的极化域显示出不同的转换路径(图4b)。在这两个域中,铁电磁滞在两个极化状态之间可逆地变化,以相同符号的大小压电响应水平表示。基于压电响应的相对幅度和偏置相关变化的符号,我们可以分配相关的极化相位。在第一个区域( 1)中,在施加到尖端的正电压(负电场)下,极化从切换到状态。与此相反,第二个区域( 2)在正电压下显示了从到的稳定切换。这些结果表明,极化是可逆的,并且偏置可用于在 和相之间交叉。这意味着可以通过电场访问所有四个势能最小值,并且状态的铁电切换涉及状态。因此,相不能视为独立的双阱铁电相,这使成为四阱铁电体,而不是两个双阱铁电体。在电容器和其他PFM研究中,观察到对称极化环路可以通过仅涉及
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[409423],资料为PDF文档或Word文档,PDF文档可免费转换为Word


