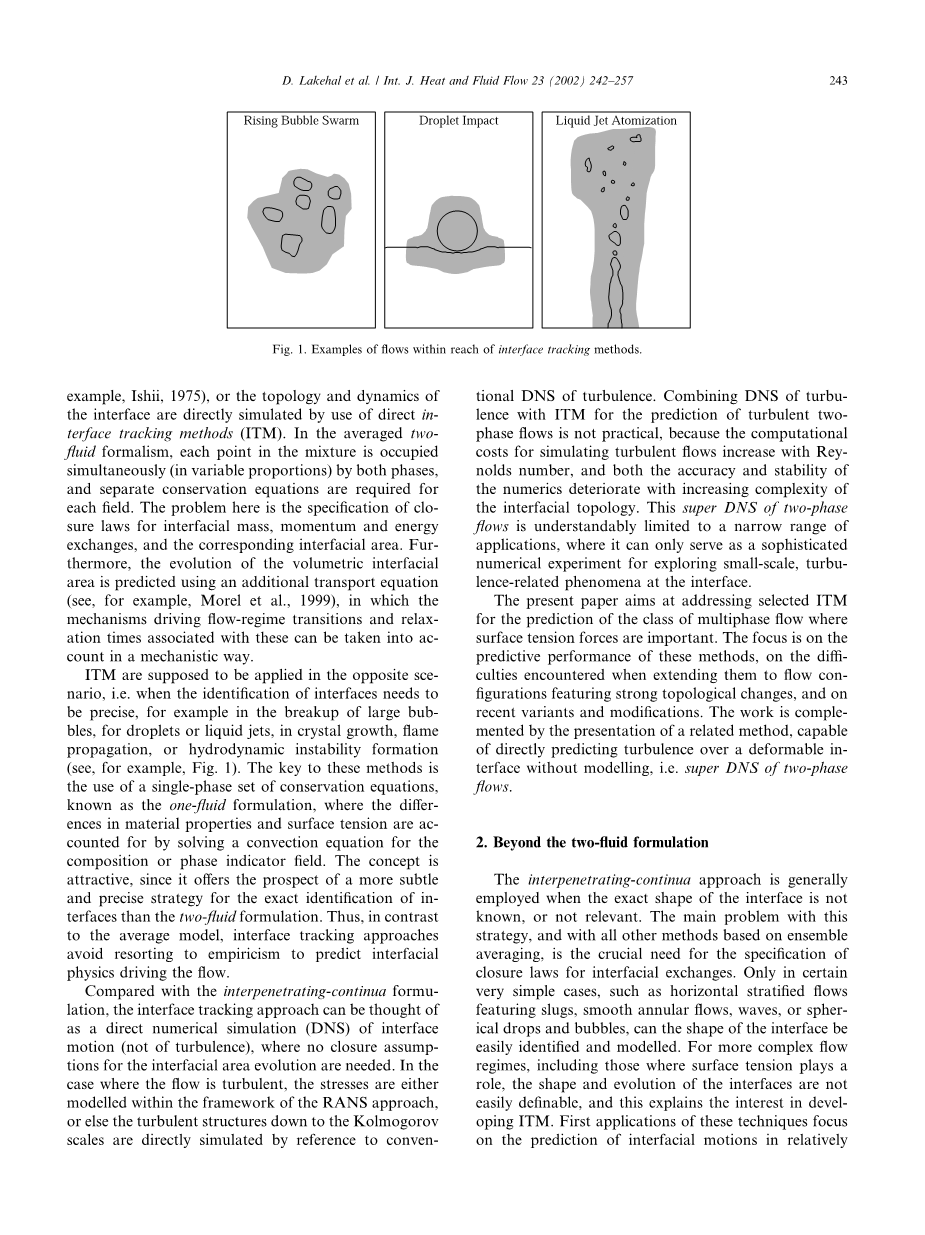
英语原文共 16 页,剩余内容已隐藏,支付完成后下载完整资料
界面跟踪直接模拟多相流中的热量和质量转移
- Lakehal , M. Meier, M. Fulgosi
苏黎世瑞士联邦理工学院能源技术研究所,ETH-Zentrum / CLT,CH-8092瑞士苏黎世新能源技术研究院,科技苏黎世的瑞士联邦理工学院,ETH-Zentrum酒店/ CLT,CH-8092瑞士苏黎世
摘要
本文介绍了近期多相直接数值模拟预测方法的发展趋势基于单流形式与各种接口跟踪算法相结合的流程。这些方法基于解决问题用于整个计算域的单组运输方程,并将不同阶段视为具有变量的单一流体
材料特性。通过平衡相位指示函数来考虑这些属性的变化。界面交换
通过将合适的来源添加为delta函数或合成域的平滑渐变,可以合并术语跨界面。这些策略首先在等温阶段讨论,然后讨论特征间相互作用的情况,相传热和传质。讨论了毛细力的处理等各个方面,并通选定的例子进行了支持展示了作者目前的工作取得的最新进展。Oacute;2002出版Elsevier Science Inc.
关键词:多相流; 单流体配方; 流体量; 水平集; 边界合并; 传热传质
- 介绍
多相流出现在自然和工业领域各种形式的过程,通常以阶段间为特征传热和传质。 例子包括蒸发 - 在自然环境中或在自然环境中分散的相燃烧室,蒸汽在动力中凝结生产部件,机翼和叶片侵蚀,液态金属喷雾剂,可溶性气体在at-大洋 - 海洋界面等。现在,目前正在进行相当大的努力澄清移动中的相间转移机制接口使用直接计算方法,没有使用模型。 这对于所有类型都是不可能的多相流动,但对于流动的类别来说,阶段可以清楚地相互区分,
(例如参见图1)。 对这些新兴趣感兴趣方法是由以下事实决定的:早期的,基于平均值的模型往往不能在工程中产生精确的解决方案感。
解决管子的Navier-Stokes方程运动的多个阶段的模拟真实问题已被证明是复杂的。 这解释了与此相比,这门学科进展相对缓慢经典的计算流体动力学应用于单相流体动力学,相流。 什么使计算多相科学尤其具有挑战性,相互作用的现象:污染物或喷雾分散与分层管道分离几乎没有什么共同之处,流动,并且几乎没有与Spinodal分解二元流体。 预测CO2的方式
吸收海洋消费者从处理蒸发 - 尽管这两种现象都是波浪形成的密切相关。 因此,预测策略必须是为特定的目标和这个领域的研究量身定制在其方法中可变
中心到多相的数值模拟流程是接口动态的准确识别通过它可以定义流动状态,可以量化特德相间转移机制。在现在的建模策略现象发生在界面分离阶段进行建模在互相贯穿的框架内
方法,也称为双流体方法(例如参见Ishii,1975),或拓扑和动力学该界面直接通过使用直接在线模拟来模拟,界面跟踪方法(ITM)。在平均两年期间,流体形式主义,混合物中的每一点都被占据两个阶段同时(以可变比例)并且需要单独的守恒方程每个领域。这里的问题是关于界面质量,动量和能量的闭合定律的规范交流以及相应的界面区域。此外,体积界面的演变使用额外的运输方程预测面积(参见,例如,Morel等,1999),其中机制推动流动政权转型和放松 - 与这些相关的时间可以被考虑进来以机械方式计算。
ITM应该应用于相反的场景,即当接口的标识需要精确时,例如分解大气泡,液滴或液体射流,晶体生长,火焰传播或流体动力学不稳定性形成(例如参见图1)。 这些方法的关键是使用单相保守方程组,称为单流体配方,其中材料性质和表面张力的差异通过求解对流方程组成或相位指示字段。 这个概念是有吸引力的,因为它提供了一个更微妙的前景并且精确确定界面的策略比双流体配方更精确。 因此,相反到平均模型,界面跟踪方法避免诉诸经验主义来预测界面物理驱动流动。
与互贯连续公式相比,可以考虑界面跟踪方法作为接口的直接数值模拟(DNS)运动(不是湍流),其中不需要关于界面区域演化的闭合假设。在流动是湍流的情况下,压力也是在RANS方法的框架内建模,否则湍流结构下到柯尔莫哥洛夫通过参考传统的湍流DNS直接模拟尺度。 将湍流的DNS与ITM结合以预测湍流两相流是不实际的,因为计算模拟湍流的成本随着雷诺数的增加而增加,并且精度和稳定性都有所提高数值随着复杂度的增加而变差界面布局。这个两相流的超级DNS可以合理地限制在一个狭窄的应用程序范围内,它只能作为一个复杂的应用程序用于探索界面处小尺度湍流相关现象的数值实验。本文旨在解决选定的ITM用于预测表面张力很重要的多相流的类别。重点是这些方法的预测性能,将它们扩展到具有强拓扑变化的流体配置时遇到的困难以及最近的变体和修改。这项工作由相关方法的介绍加以补充直接预测可变形界面上的湍流而无需建模,即两相流的超级DNS。
- Beyond the two-fluid formulation
当界面的确切形状未知或不相关时,通常采用互穿连续方法。
这个策略的主要问题,与基于集合平均的所有其他方法相结合,是关于界定交换界限的关闭法律的关键需求。只有在某些非常简单的情况下,例如以蛞蝓为特征的水平分层流体,光滑的环形流体,波浪或球形滴体和气泡,界面的形状才能被容易地识别和建模。对于更复杂的流体状态,包括表面张力起作用的状态角色,界面的形状和演变并不容易确定,这就解释了开发ITM的意义。这些技术的第一个应用集中在相对简单的情况下界面运动的预测,如一个相内含物的稳定性,如大气泡,液滴或液体射流的分解(图1)。
2.1。 单流体配方的连续性方程
控制两相流系统的精确的或微观的瞬时方程可以正式写成分量指示函数或组合场,在时间t和点x,由定义知=1时xisin;k相,否则=0.由于Xk是随着流动而产生的性能,其材料衍生物显然为零(德鲁和帕斯曼,1999年)
. (1)
这被称为描述用Xk标记的表面的运动的拓扑方程,随速度u移动。特别要注意的是,由于Xk的不连续性(跨接口)使其成为非可导函数,所以这是该问题的弱表述。在没有传热和传质的情况下,两个不混溶的接触相(例如液体L和气体G)的质量平衡方程包含如图2所示在体积V内可写为
(2)
(3)
其中L表示液体密度,G表示气体密度。 上述方程组可以以更方便的形式重新表达 (4)
(5)
在两流体公式中,方程(4)和(5)首先被适当地平均(例如,过量的体积,如图2(左)所示)。然后同时解决它们,同时还有每个阶段的动力和能量方程。然而,在单流体变体中,上述方程组可以结合在一起这是一种通向单一守恒方程的途径,但具有由界面位置决定的可变密度rho;。这是通过组合等式(4)和(5)获得的。
(6)
使用等式(1)并取part;trho;L和part;trho;G相同不可压缩流体的零点简化为等式
(7)
最后将其缩小为下面的表格
(8)
这个结果很重要,因为在某些基于有限体积方法的Navier-Stokes求解器中 等式(8)一般写成,这显然与等式(6)不兼容。
2.2。 具有毛细作用力的流体的单流体配方
为了解释可测密度和粘度通过界面分离两个非混溶相,单流体法(Kataoka,1986)将其自身看作是一种自然选择。在这里,这两个阶段是由整个一组守恒定律处理流场,但明确说明了相和毛细管力的物质性质(适当时)的差异。在这种情况下,不可压缩牛顿流体的局部平衡方程为写为
(9)
(10)
(11)
其中g表示重力加速度,p表示压力,E表示内部能量,T表示温度,k表示热传导率,表示粘性应力张量,表示动力粘度 ,是毛细管应力,是控制毛细管力的强度的系数。在这些方程中,材料属性如密度局部依赖于通过使用拓扑方程(1)确定的相位指示函数Xk.
(12)
请注意,对于上述关系只能作为模型使用的粘度,情况并非如此。
毛细张量表示由于主流密度或组分场梯度而集中在二次使用界面处的能量(Anderson等人,1998)。它反映流体的自由能密度相对于组分场的变化率,即=.
这种广义形式的毛细张量可以减少到的条件传统的和简化的表面张力模型将在下面讨论。
毛细张量(实际上是自由能密度)不仅是密度等热力学性质的函数,而且也是其梯度的函数。正如Anderson(1998)等人所定义的那样。Nadiga和Zaleski(1996),Chella和Vinals(1996),这个张量具有形式
(13)
用I表示单位矩阵单位张量面积,并且可以证明
(14)
范德华力(1893)认为,毛细张量的这种特殊形式是由最简单的自由能密度模型导出的。Jacqmin(1999)在中使用了一个稍微不同的形式,因此在中使用了一个不同的形式关系(13)在假设条件下作为特定情况出现。该方法使用公式(13)给出的毛细作用力的形式结合Navier-Stokes方程被称为二阶使用界面模型(Anderson等,1998; Jacqmin,1999)。Lowengrub和Truskinovsky(1998)给出了控制二元粘性流体运动的方程组的详细描述,他称之为Navier-Stokes-Cahn-Hilliard(NSCH)模型。它们已被广泛地用于毛细作用力特别占主导地位的应用,例如, 在Anderson等人的调节分解中(1998),Jacqmin(1999)和Verschueren等人(2001年)。Chella和Vinals(1996)证明,在平滑弯曲界面薄的界限内,当界面运动与局部弛豫时间相比较慢时,方程(10)和(11)中出现的毛细源项可以 近似于
(15)
其中n表示与界面垂直的单位矢量,K是正常数,表示由下式定义的局部曲率
(16)
将等式(15)积分在界面区域(ds)上产生Brackbill等人的连续表面力(CSF)模型。(1992年)
(17)
其中是表面张力,假定为常数横跨界面子层的整个厚度,表示一个狄拉克脉冲XF是界面的即时位置。 delta函数在上面的表达式中出现,是以下公式得到
(18)
表面张力反映了毛细管的过量能量集中在单位表面的界面处面积由于在界面上的变化而引起的面积子层。
为了避免必须明确处理曲率,公式(13)的进一步处理导致Lafaurie等人 (1994)以及Scardovelli和Zaleski(1999)提出的基于CSF的毛细作用力的各向异性变体:
(19)
也称为连续表面应力(CSS)模型。CSF和CSS原则上都简单,稳健,只需要确定相场。然而,两者都可以在界面附近产生寄生电流,因为一旦离散化,界面处的确切动量跳跃条件并不总是妥善保存,即压力和粘性应力不平衡的毛细力.这部分是由于在解决曲率方面缺乏精确性,但也是如此结果来自动量方程中的表面项被离散化的方式。即便如此,脑脊液模型及其变体对各种研究人员(Kothe和Mjolsness,1992; Kothe等人,1996; Richards等人,1995; Rider等人,1995)具有吸引力,主要是因为它们简单实现。在不同的使用界面模型中的组成场被用作一个质量它具有适当的化学扩散热力学定律。因此它需要预先确定(已知)热力学的组成(或密度),或者组分场1的拓扑方程涉及的四阶导数,它考虑了所讨论的化学扩散的热力学。该模型尚未与CSF和CSS杂散电流相比较。
2.3。 基于CSF的模型的性能和影响
缓解一些与之相关的缺点CSF方法,Meier等人 (2002)开发了一个新的用于确定曲率j的技术,包括表面张力源项的方式保持低电流(称为CSF-M)。在他们的方法,通过对参考数据使用最小二乘法拟合的估计函数更准确地确定曲率,并且曲面张力被离散化以显着减小寄生电流。该方法被发现与所讨论的用于界面重建的特定算法一起使用时最小化这些电流在图3的上下文中。
所考虑的基准问题是指围绕圆形液滴的表面张力分布,其中曲率名义上是已知的并且是恒定的。详细说明了具有可变直径D 的25个液滴的光谱(用标准化)。图3比较了这种新方法CSF-M的结果与使用CSF和CSS,方程 (17)和(19获得的结果)。图3(a)显示了所得到的j的标准偏差和整个域的平均速度估计值。这揭示了使用CSF获得的曲率估计中的高水平的噪声,而Meier等人的方程 CSF-M方法实现约三至七倍更好平均曲率与参考值的一致性,以及大约四到七倍的标准偏差。此外,在与其他两种方法相比,CSF-M方法被二至三个数量级的杂散电流re FL由所述阿尔季音响ected可
全文共15226字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[13225],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。