
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
用移动DLT实现逼近投影变换的图像拼接
Julio Zaragoza, Tat-Jun Chin, Quoc-Huy Tran, Michael S. Brown, and David Suter
摘要:商业图像拼接软件的成功常常让人们以为图像拼接是一个“已解决的问题”。然而,事实上,当输入的照片违反了相当严格的成像假设,尤其是这些照片是纯粹因旋转而不同的视图,或者图像场景实际上是平面时,许多软件给出的结果并不令人满意。 这些假设是2D投影变换或基于单应性的图像拼接的基础,但在临时用户的手中,这些条件经常被违反,从而产生未对准的图像或结果中的“鬼影”。因此,许多现有的图像拼接软件严重依赖于后处理程序来隐藏鬼影.。本文提出了一种新的技术:移动直接线性变换,简称DLT。 它能够调整或微调投影的变换,以适应输入数据与理想条件的偏差。能减少鬼影且不损害图像拼接的几何真实感。因此,此技术减少了对潜在昂贵的后处理算法的依赖。此外,我们还描述了如何利用光束平差法同时校正多个投影的变换,以精确地进行大全景图像拼接。
关键词:图像拼接,图像对齐,投影变换,直接线性变换,移动最小二乘法
1.介绍
图像拼接算法已经到了一个成熟的阶段,现在有大量的基于图像拼接技术或结合图像拼接技术的商业软件。著名的图像处理软件如AdobePhotoshop(简称PS),基于web的照片组织软件如microsoft Photosynth,智能手机应用程序如Autostich,以及内置图像拼接功能的数码相机等。这些软件在帮助用户排版和欣赏照片方面非常有用。图像拼接技术的成功可能会让人们以为图像拼接技术已经被攻克了。但是事实上,当输入为非理想数据的时候,许多软件都不能给出令人信服的结果。
大多数图像拼接算法的步骤都较为相似:首先,估计图像的变换矩阵,使重叠的区域对齐,然后将对齐配准的图像合并到一个共同的图像坐标系上。当然,在现实生活中,数据的完美对齐是很少的,因此,大多数的研究工作都着重于设计更好的对齐或合成技术上,以减少或隐藏未对准的区域。最先进的算法可在[2]中看到。本文的工作集中在改进图像对准阶段。
这与之前简要提到的图像拼接最先进的合成技术是相关联的。其中最主要的是缝切割方法[3]、[4],它优化了重叠图像中的像素选择,减少了可见的拼接缝;以及先进的像素融合技术,如拉普拉斯金字塔混合技术[1],[5]和泊松图像混合[6],它减少了因失调或暴光差异造成的模糊。虽然这类后处理程序对产生视觉上可接受的结果是很重要的,但它并不完美,而且可能不会一直工作。(参见[7]为例)。因此,在对齐步骤中尽量减少错误是亟待解决的。
图像拼接对齐问题的研究,使光束平差法[8]的应用达到顶峰,同时也优化了输入图像的相对旋转[1],[9],它用一个通用的参考框架将所有图像对齐。这是如[1]中所描述的Autostich中使用的技术。早期的工作逐步变换了多个图像,其中,每一幅图像都有一系列的对齐函数,将图像投影到公共参考框架上[10],[11]。因此,重点在于找到线程处理的最佳顺序,这样错误就不会被过度传播和放大。
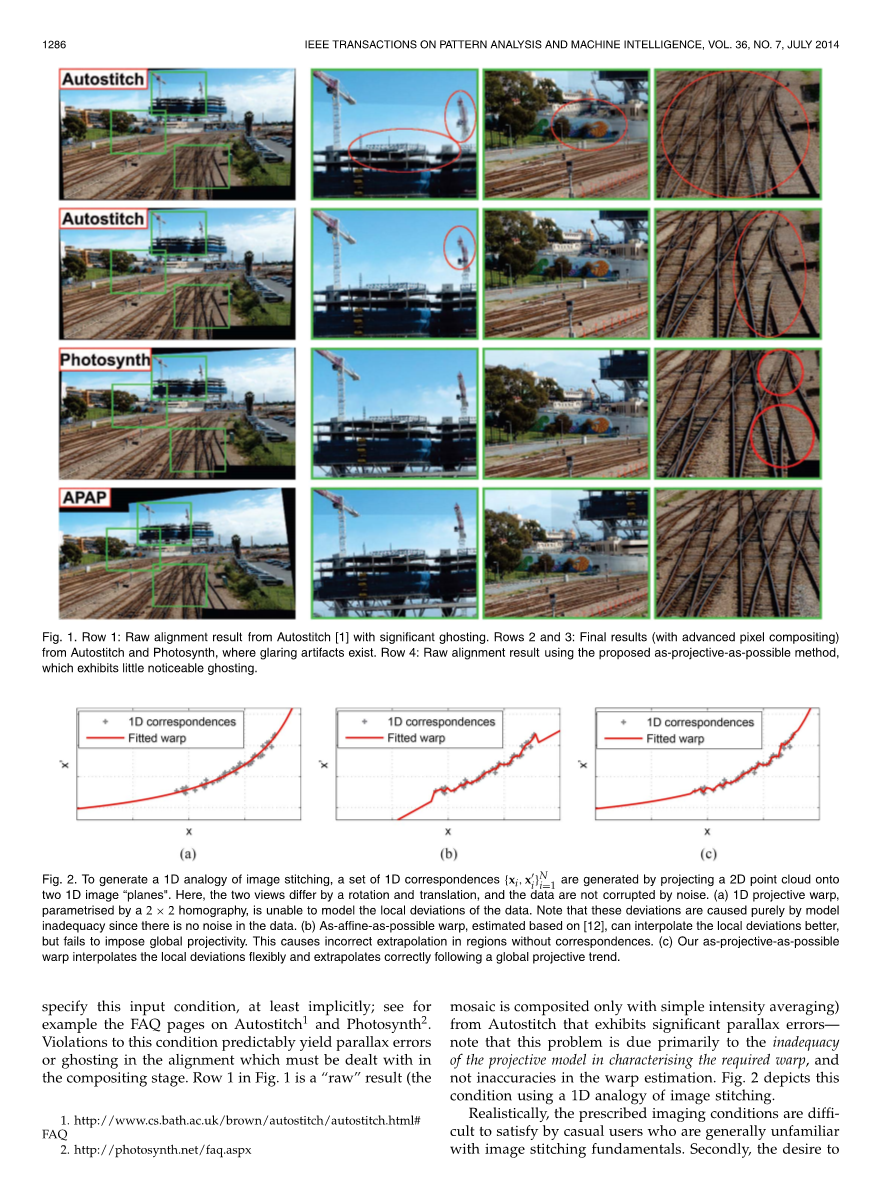
有趣的是,目前的大多数技术(包括Autostich和Photosynth)都将对齐函数建模为二维投影变换或单应性矩阵。只有当图像与纯旋转不同的视图相对应,或者成像场景实际上是平面的(例如,当场景足够远时[2]),单应性矩阵才是正确的。事实上,许多商业图像拼接软件或隐或明的都指定了这个输入条件,例如Autostitle1和Photosynth2上的FAQ页面。违反这一条件,就会产生视觉差或产生对齐中的鬼影,故必须在合成阶段处理。图1中的第1行是来自Autostich的一个“原始”结果(图像拼接仅用简单的灰度平均合成),有显著的视觉差。请注意,这个问题主要是由于以下原因造成:投影模型描述所需变形不完善,以及在变形度估计中的不精确性。图2使用图像拼接的一维类比来描述这种情况。
图1.第1行:Autostitch[1]的原始对齐结果,有明显的鬼影。第2行和第3行:来自Autostich和Photosynth的最终结果(采用高级像素合成),有明显的图像失真。第四行:使用所提出的逼近投影的方法后的原始对齐结果,几乎没有明显的鬼影。
图2.为了产生图像拼接的一维类比,通过将二维点群投影到两个一维图像“平面”上,生成一组一维对应。在这里,两个视图因旋转和平移而不同,并且数据不会被噪声破坏。(a)用2times;2的单应性矩阵的一维投影变换无法模拟数据的局部偏差。注意,这些偏差纯粹是由于模型不合适引起的,因为数据中没有噪音。(b)根据[12]中的逼近投影变换,可以较好地插入局部偏差,但不能提高全局投影性,这导致在没有对应关系的区域内会进行不正确的推断。(c)本文的逼近投影变形插入的局部偏差灵活,并能正确地推断出一个整体投影趋势。
实际上,对于一般不熟悉图像拼接基本原理的普通用户来说,规定的成像条件是难以满足的。其次,当无法在所需的成像条件下重新访问场景时,才会想到要对图像进行拼接。不幸的是,许多最先进的技术,即使使用先进的像素合成或后处理,如果给出不合适的数据,也不能产生令人满意的结果。图1中的第2行和第3行是Autostich1和Photosynth2,的最终(后处理)结果,仍然存在明显的图像失真。
上述问题为改进图像拼接的对准方法提供了强大的动力。具体来说,我们认为基于单应性矩阵的对齐必须考虑到不满足假设成像条件的图像。为此,我们提出了一种新的单应性矩阵估计技术——移动DLT,它能够调整或微调单应性矩阵,以说明偏离预期趋势的数据,从而实现逼近投影变形。图1中的第4行显示了原始对齐结果,图2则为逼近投影变换。该方法在不影响场景几何合理性的前提下,显著减小了对齐误差。
请注意,我们的目标不是消除去鬼影算法的使用,如果存在严重的失调或移动的对象,这些算法仍然非常有用。然而,我们认为,实现精确的图像对齐是必要的,因为这会大大降低对后续处理的依赖。
我们工作的早期版本[13]引入移动DLT进行图像拼接。在这里,我们提出了一种新的光束平差技术法,可以同时改善大全景图的多重逼近投影偏差。
论文的其余部分组织如下:第二节概述了重要的相关工作,第三节介绍了提出的方法及其基本原则,第四节扩展了全景生成的方法,第五节介绍了得出的结果,第六节阐述了得出的结论。
2相关工作
在照像机任意移动的情况下考虑图像拼接的方法,一个值得注意的例子是基于流行的图像处理[14],这是基于推扫式的相机。使用标准透视相机,推扫式相机可以通过连续“扫描”视频中的场景来近似。然而,该方法可能不适用于“离散”照片集中的静态图像,例如由Autostitch和Photosynth处理的图像。
2.1三维重建与平面加视差
从理论上讲,给定一组场景的重叠视图,可以首先恢复三维结构和照像机参数(例如,通过SfM和立体匹配),然后将每一个场景点重新投影到一个更大的参考图像上,以产生拼接图像。一个值得注意的方法是[15],它提供了从长街场景拍摄的图片中的全景图。然而,如果我们的目标是仅仅图像拼接的话,那么一个完整的3D方法可能会“过度”;事实上,许多先进的合成方法如[3]、[6]都只专注于创建符合标准的拼接图像,而不考虑3D结构。另外,三维重建只适用于重叠区域的场景点。此外,SfM在视图中可能很脆弱,基线很小(但不是完全为零),这代表了现实生活中许多的图像拼接情况。
中级方法是使用具有视差分量的平面投影映射[16]直接对齐图像。在不进行全三维重建的情况下,它们的方法只能在每个像素上近似视差[16],这仍然会导致显著的视觉差。
2.2全景创建
给出一组重叠的图像,用最先进的方法[1],[9]进行光束平差[8],可优化所有视图的焦距和相机姿态(相对旋转),这就产生了图像间的光束平差来执行对齐。Shum和Szeliski[9]根据像素值(在定期取样的图像块位置)定义误差项,布朗和洛[1]使用SIFT关键点对应[17],布朗和洛[1]还引入了一个基于SIFT匹配的全景识别步骤,该步骤能够确定属于同一全景图的图像子集,给定一个无序的照片集。
第二个精确阶段也在[9]中提到,说明了图像拼接中的局部失调。对于每个图像块位置,从每个视图中获取反投影射线的平均值,然后再将其投影到每个视图上,以获得2维中所需的补丁位置。然后针对原始和期望的图像块位置之间的差异进行插值(例如,使用样条)以形成用于消除视觉差的校正场。然而,与直接改进投影偏差的方法相比,这种两步方法是很麻烦的。两步方法还引发了关于整个过程的最优性的问题,例如,如何使校正场不过度扭曲原始投影变换。通过直接估计逼近投影变形,我们的方法避免了单独的细化步骤.
其他工作不是估计相对图像的旋转,而是直接估计图像间的单应性矩阵,然后用这些链或线程单应性矩阵将多幅图像拼接到一个共同的参考框架上[10],[11]。因此,重点是找到最佳的线程顺序,使得错误不会被过度传播和放大。这些单应性矩阵也可以通过在三组矩阵[11]之间施加几何一致性来加以细化。然而,对单应对齐的依赖意味着这种线程处理方法不能处理非理想的数据。
2.3挠性变换的直接估计
与我们的工作更接近的是最近的方法,这些方法背离了传统的单应性模型。提出了一种用于图像拼接的平滑变化的仿射变换[18]。从基于运动相干的点集回归方法[19]开始,仿射初始化[18],然后局部变形,将注册错误最小化,同时保持全局亲和力。从概念上讲,这种变换与图像变形中逼近投影的仿射变换相似[12]。然而,从根本上讲,使用仿射调整可能不是最佳的推断,因为亲和力不足以实现透视图的变形[2],例如,仿射变换可能会在外推区域产生反效果的预并行。因此,虽然该方法可以灵活、准确地进行局部自适应插值,在外推时可能产生失真的结果;观察拼接结果中的图像内容[18]如图6和图7的第2行所示。
图3.对于一维合成图像拼接问题,在没有调整的情况下移动DLT的结果。
在视频稳定的背景下,Liu等人[20]预先提出了保护内容的变换算法。给定原始图像帧与稳定图像帧之间的匹配点,新视图是通过使用尽可能相似的变换来扭曲原始图像合成的[21],这使注册错误最小化,并保持了场景的刚性。该方法还对原始图像进行了单应性预处理,从而有效地产生了局部自适应的单应性矩阵。施加场景刚度使视频稳定中的“摆动”效应最小化。然而,在图像拼接中,由于刚性约束,图像拼接中存在较大的旋转和平移差异,它们的插值方法不够灵活。但这应该不是一个问题[20],因为原始平滑的摄像机路径是接近的(见[20]第4节),即对齐之间的移动很小。
通过假设场景包含一个地面平面和一个遥远的平面,高等人[22]提出了用于图像拼接的对偶单应性变换。基本上,这是一种特殊的分段单应性矩阵,它比使用单一的单应性矩阵更灵活。如果所需设置为真,则它的性能很好,但对于任意场景,可能很难扩展该方法,例如,如何估计适当数目的单应性矩阵及其参数。
值得注意的是,与所提出的方法不同的是,上述灵活的图像对齐方法没有为多个图像拼接提供同时的细化步骤。因此,在创建大型全景时,结果的质量在很大程度上依赖于两两拼接和对齐函数链接顺序的准确性。
3逼近投影变换
在这一部分中,我们首先回顾了二维投影变换在图像拼接中的应用。然后,我们描述了我们方法的基本原理。
3.1二维投影变换
设x=[x y]T和xrsquo;=[xrsquo; yrsquo;]T是交叉图像I和Irsquo;之间的匹配点。投影变换x到xrsquo;遵循关系
(1)
图4.用我们的方法演示图像拼接。输入图像是通过旋转和平移而不同的视图,图像大小均为1500times;2000。在RANSAC为2100之后,SIFT匹配{xi, xi}Ni=1(未显示)。(a)目标图像I;(b)源图像I,为100times;100个单元(清晰绘制的仅为25times;25);(c)用转化后的单元覆盖对齐图像,使变换可见。可观察到,变换是全局投影的外推,但在重叠区域匹配良好,可以更好的对齐。(d)(b)中单元的加权数直方图=gamma;.
其中xtilde; = [xT 1]T,在齐次坐标下是x,~表示大小相等。将3times;3矩阵H称为单应性矩阵,在非齐次坐标中,
(2)
其中rj是H的第j行。在(2)中的除法导致2D函数是非线性的,这对于允许完全透视偏差是至关重要的。图2(a)给出了一维类比。
直接线性变换(DLT)[23]是从一组噪声点匹配的I和Irsquo;之间估计H的基本方法。(例如,利用SIFT特征匹配建立[17])。首先,(1)被重写为隐式条件03times;1=xtilde;times;Hxtilde;,然后线性化为 全文共19587字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11319],资料为PDF文档或Word文档,PDF文档可免费转换为Word


