
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
Mean teachers是更好的任务模型:加权平均的一致性目标改进半监督深度学习结果
摘要
最近提出的时间整合法(Temporal Ensembling)已经取得了在几个超级学习基准中最先进的成果。它在每个训练样本上保持标签预测的指数移动平均值,并且对与该目标一致的预测进行惩罚。然而,因为目标每个最大训练次数中只能改变一次,所以时间整合方法在学习大型数据集的时候变得难以运作。为了解决这个问题,我们提出了平均教师法(Mean Teacher),这是用一种平均权重模型取代标签预测的方法。平均教师法更多的好处在于,它提高了测试的准确性,并且在进行训练时所需使用的标签比时间整合法更少。在不改变网络架构的情况下,平均教师法在具有250个标签的SVHN数据集上实现了4.35%的错误率,优于用1000个标签训练的时间整合法。我们还发现,一个良好的网络架构对于算法执行和性能至关重要。通过结合平均教师法和残差网络,我们将有4000个标签的CIFAR-10数据集的技术水平从10.55%提升到了6.28%,将有10%标签的ImageNet2012数据集的技术水平从35.42%提升到了9.11%。
1 引言
深度学习已经在图像和语音识别等领域取得了巨大成功。为了学习有用的抽象模型,深度学习模型需要大量的参数,因此容易过度设置(如图1a)。此外,手动向训练数据添加高质量标签通常十分昂贵。因此,需要使用正则化方法来有效利用未标记的数据,以减少半监督学习中的过度设置。
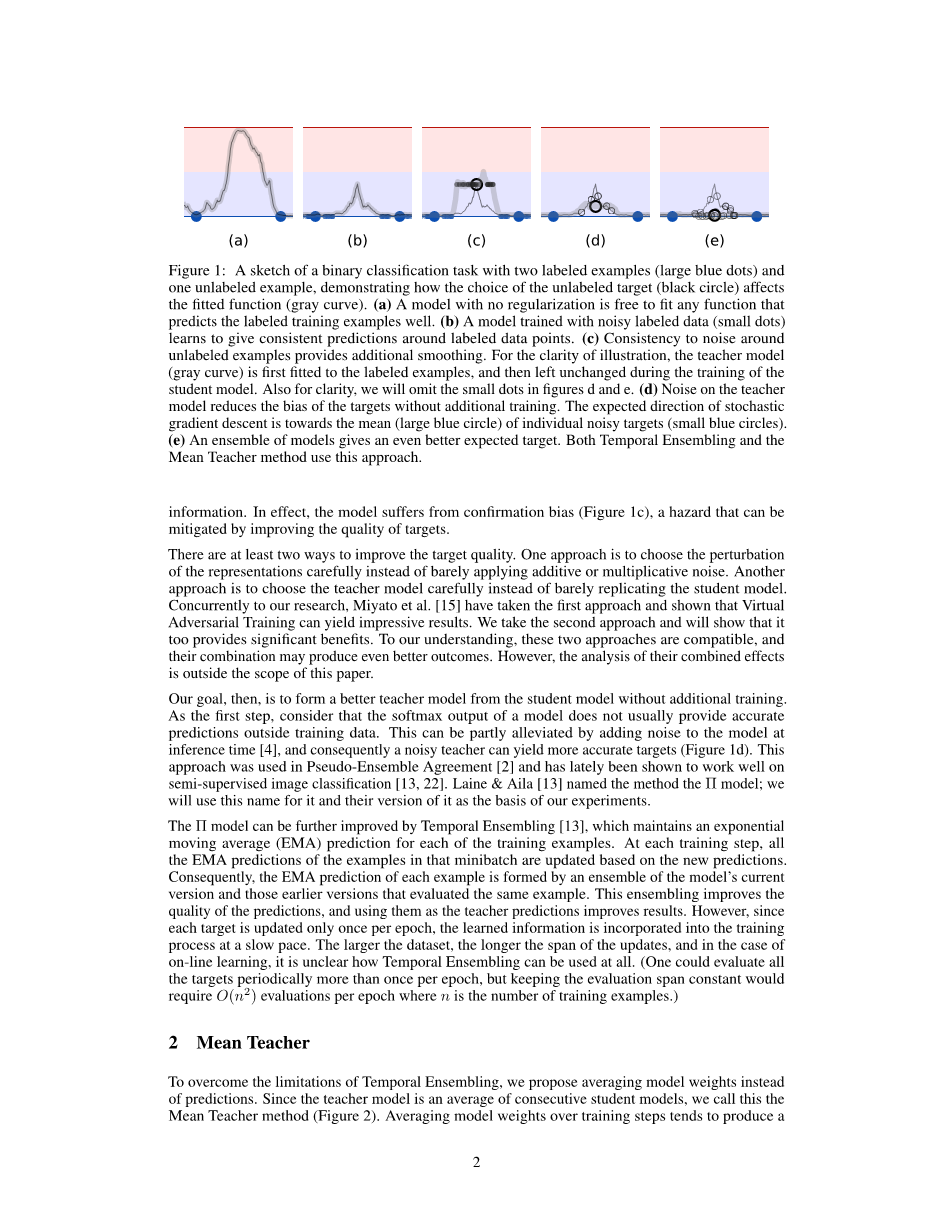
当感知有轻微改变时,人类通常仍然认为感知对象是同一个物体。相应地,分类模型应该支持为相似数据点提供输出一致的函数。实现这一点的一种方法所示给模型的输入增加噪声。为了使模型能够学习更加抽象的不变性,可以将噪声添加到中间表示中,例如Dropout算法[27]。正则化模型最小化每个数据点周围的流形上的成本,而不是最小化输入空间的零维数据点的分类成本,从而将决策边界推离标记的数据点(如图1b)。
由于分类成本对于未标记的例子是未定义的,噪声正则化本身并不能帮助半监督学习。为了克服这一点,Gamma;模型[20]评估了每个数据点在有噪声和无噪声的情况,然后在两种情况下的预测之间应用一个一致性成本(consistency cost)。在这种情况下,模型扮演了教师和学生的双重角色。作为学生,它像以前一样进行学习;作为教师,它生成随后被自己作为学生用于学习的目标。由于模型本身生成目标,它们很可能是不正确的。如果对生成的目标给与过多的权重,不一致性的代价会超过错误分类的代价,从而阻碍模型学习新的信息。实际上,这个模型存在着确认偏差(如图1c),这种风险可以通过提高目标的质量来减轻。
可以提高目标质量的方法至少有两种。一种方法是仔细选择表示的扰动,而不是仅仅用加法或乘法添加噪声。另一种方法是仔细挑选教师模式,而不是仅仅复制学生模式。在我们进行研究的同时,Miyato et al.[15]采取了第一种方法,并展示出虚拟对抗训练(Virtual Adversarial Training)可以产生令人印象深刻的结果。我们则采用了第二种方法,并且将展现第二种方法也提供了显著的好处。在我们的理解中,这两种方法是可兼容的,两种方法的结合可能会产生更好的结果。然而,对其综合效益的分析不在本文的讨论范围内。
因此,我们的目标是在没有额外训练的情况下,从学生模式中构创一个更好的教师模式。首先第一步,考虑到softmax函数输出通常不能训练数据之外提供准确的预测,这可以通过在推断时间[4]向模型添加噪声来部分缓解,因此,有噪声的教师模式可以产生更精确的目标(如图1d)。这种方法被用在伪系综协议(Pseudo-Ensemble Agreement)[2]中,并且最近被证明在半监督图像分类[13,22]中工作良好。莱恩和艾拉(Laine amp; Aila)[13]将这种方法命名为Pi;模型;我们将在研究中使用这个命名并且把他们的版本作为实验的基础。
图1:一个二进制分类任务的草图,包括有两个标记示例(大蓝点)和一个未标记示例,演示了未标记目标(黑色圆圈)的选择如何影响拟合函数(灰色曲线)。
- 一个没有正则化的模型可以自由地拟合任何能很好地预测标记训练样本的函数。
- 用噪声标记数据(小点)训练的模型学会在标记数据点周围给出一致的预测。
- 未标记示例周围噪声的一致性提供了额外的曲线平滑。为了说明能够更加清楚,教师模型(灰色曲线)首先被设置为标记的例子,然后在学生模型的训练过程中保持不变。同样为了清楚起见,我们将忽略图d和图e中的小点。
- 无需额外的训练,教师模型上的噪声减少了目标的偏差。随机梯度下降的与其方向朝向单个噪声目标(蓝色小圆圈)的平均值(蓝色大圆圈)。
- 模型的整合给出了更好的预期目标。时间整合法和平均教师法都使用的这种方法。
Pi;模型可以通过时间整合法(Temporal Ensembling)[13]来进一步改进,这里的时间整合所做的就是对每个训练示例维持指数移动平均(EMA)预测。在每个训练步骤中,该小批次中所有示例的EMA预测都是基于新预测更新的。因此,每个示例的EMA预测都是由模型的当前版本和评估相同示例的早期版本的集合而形成的。这种整合提高了预测的质量,并且,将它们用作教师模式的预测可以改善结果。然而,由于每个目标在每个时期仅更新一次,所以所学习的信息以缓慢的速度被并入训练过程。数据集越大,更新的跨度就越长,并且在在线学习的情况下,时间整合是怎样使用的根本还是不明确的。(每个时期可以定期评估所有目标一次以上,但是保持评估跨度恒定需要每个时期进行次评估,其中n是训练示例的数量。)
2 平均教师法(Mean Teacher)
为了克服时间整合的局限性,我们提出了用平均模型权重代替预测。由于这个教师模型是连续学生模型的平均值,我们称之为平均教师法(如图2)。在训练步骤中平均模型权重往往会产生一个比直接使用最终权重更精确的模型[18]。我们可以在训练中利用这一点来构建更好的目标。教师模型使用的是学生模型的EMA权重,而不是与学生模型共享权重。现在它就可以在每一步之后而不是每一个时期之后就聚集信息。此外,由于权重平均值改善了所有的层的输出,而不仅仅是顶层输出,因此目标模型具有更好的中间表示。相对于时间整合法,这些方面带来了两个实际优势:第一,更精确的目标标签导致学生模型和教师模型之间更快的反馈循环,从而导致更好的测试准确性。第二,这种方法可以扩展到大型数据集和在线学习。
图2:平均教师法。该图描述了一个带有当个标签示例的培训批次。学生模型和教师模型都在计算中评估了输入应用噪声(,)。学生模型的softmax函数输出与使用分类成本的单热标签和使用一致性成本的教师模型输出相比较。在用梯度下降更新学生模型的权重之后,教师模型的权重被更新为学生权重的指数移动平均值。两种模型的输出都可以用于预测,但是在训练结束时,教师模型的预测更有可能是正确的。除了不应用分类成本的情况之外,带有未标记示例的训练步骤是相似的。
更正式地说,我们将一致性成本J定义为学生模型(权重为,噪声为)预测和教师模型(权重为,噪声为)预测之间的预测距离。
Pi;模型法,时间整合法和平均教师法这三种方式之间的区别在于教师预测是如何产生的。鉴于在Pi;模型中采用的是,在时间整合方法中采用连续预测的加权平均值逼近,我们在训练步骤t将定义为连续权重的EMA。
其中是平滑系数超参数。这三种算法至今的另一个区别是,Pi;模型将训练应用于,而时间整合和平均教师则将其视为优化方面的常数。
我们可以通过用随机梯度下降对噪声,的每个训练步骤进行抽样采样来近似一致性代价函数J。跟随莱恩和艾拉的研究,我们在大多数实验中使用均方误差(MSE)作为一致性成本。
表1:SVHN数据集在10次运行(使用所有标签运行4次)时的错误率百分比。我们在评估所有模型时采用指数移动平均权重。所有的方法都使用相似的13曾ConvNet架构。不增加输入的结果见附录中的表5。
表2:CIFAR-10数据集在10次运行(使用所有标签运行4次)时的错误率百分比
3 实验
为了验证我们的假设,我们首先在TensorFlow[1]中复制了Pi;模型作为我们实验的基线。我们随后修改了基线模型以使用加权平均一致性目标。模型架构是一个13层的卷积神经网络(ConvNet),其具三种类型的噪声:输入图像的随机平移和水平翻转,输入层上的高斯噪声(Gaussian noise)以及网络内应用的压差。我们使用均方误差作为一致性成本,并在前80个时期将其权重从0提升到最终值。附录B.1中描述了模型和训练程序的细节。
3.1 在SVHN数据集和CIFAR-10数据集上其他方法的比较
我们使用街景房号(SVHN)数据集和CIFAR-10基准[16]进行了实验。两个数据集都包含了属于十个不同类别的32times;32像素的RGB图像。在SVHN数据集中,每个例子都是一个门牌号的特写,这个类代表图像中心数字的身份。在CIFAR-10数据集中,每个示例都是属于一个类(例如马、猫、汽车和飞机)的自然图像。CIFAR-10数据集由50000个训练样本和10000个测试样本组成。
表1和表2比较了最新方法的结果。比较中的所有方法都使用相似的13层ConvNet架构。平均教师法在半监督SVHN数据集任务中较Pi;模型法和时间整合法而言提高了测试精度。平均教师法还在我们的基准Pi;模型的基础上改善了CIFAR-10数据集的结果。
Miyato et al.[15]最近出版的《虚拟对抗训练》在1000标签的SVHN数据集和4000标签的CIFAR-10数据集上的表现甚至优于平均教师法。正如引言中所讨论的,虚拟对抗训练(VAT)和平均教师法是可以互补的方法。两种方法的结合可能比单独使用两种方法产生更好的准确性,但是这种研究超出了本文的范围。
表3:在有额外未标记训练数据的SVHN数据集上10次运行的错误百分比
图3:在最初的100000个训练步骤中,平均教师法的平滑的分类成本(顶部)和分类误差(底部)以及我们在SVHN数据集构建的基线Pi;模型。在上面的一行中,训练分类成本仅使用标记数据进行测量。
3.2 具有额外未标记数据的SVHN数据集
根据上面的分析,我们认为平均教师法可以很好地适应大数据集和在线学习。此外,SVHN数据集和CIFAR-10数据集的结果也表明,平均教师法可以有效地使用未标记的例子。因此,我们想测试以下我们所用的方法是否已经达到了极限。
除了初级训练数据,SVHN数据集还有一个包括了531131个示例的额外数据集。我们从初级训练中选了500个样本作为我们的标记训练示例。我们用初级训练数据集的其余示例与额外数据集中的示例一起作为未标记示例。我们用平均教师法和基线Pi;模型法进行实验,并且分别使用了0,100000或500000个额外示例。表3展示了本次实验的结果。
3.3 对训练曲线的分析
图3中的训练曲线可以帮助我们理解使用平均教师法的效果。正如预期,在初始阶段后,EMA加权模型(底部一行的蓝色和深灰色曲线)给出的预测比单纯的学生模型(橙色和浅灰色)的预测更准确。使用EMA加权模型作为教师模型可以改善半监督设置下的结果。教师模型(蓝色曲线)通过一致性成本改善学生模型(橙色曲线),学生模型则通过指数移动平均值改善教师模型,这看来是一个良性的反馈循环。如果这个反馈周期被分离,学习会更慢,模型会更早开始溢出(深灰色和浅灰色曲线)。
在数据集标签稀缺的情况下,平均教师法能够有所帮助。当使用500个标签(中间栏)时,平均教师法学习的更快,并且在Pi;模型法停止改善后还能够继续训练。另一方面,在全标签的情况下(左栏),平均教师法和Pi;模型法的行为几乎完全相同。
图4:有250个标签的SVHN数据集在每个超参数设置及其平均值的四次运行中的验证错误。在每次实验中,我们改变一个超参数,其余的使用表一的评估来运行超参数。评估运行中使用的超参数设置用粗体字标记。相关详细信息,请参见文本。
平均教师法相较于Pi;模型法能更有效地使用未标记的训练数据,如中间栏所示。另一方面,有了500k个额外的未标记示例(右栏),Pi;模型法会持续改善更长的时间。平均教师法学习更快,并且最终能收敛得到更好的结果,但是数据的绝对数量似乎弥补了Pi;模型法更坏的预测。
3.4 消融实验(Ablation experiments)
为了评估模型各个方面的重要性,我们对有250个标签的SVHN数据集进行了实验,在保持其他参数不变的情况下,一次改变一个或几个超参数。
消除噪音(图4(a)和图4(b))。在引言和图1中,我们提出了这样一个前提假设:Pi;模型通过在模型的两侧添加噪声可以产生更好的预测。但是,在添加使用了平均教师法后,噪声还需要么?是的。我们可以看到,输入增加或输出下降对于可通过的运行都是必要的。另一方面,当使用增加时,输入噪声并没有帮助。教师模型方面的输出减少只对学生模型方面的输出减少有一点点的好处,至少在使用输入增加的情况下如此。
对均方差衰减和一致性权重的敏感性(图4(c)和图4(d))。平均教师算法的主要超参数是一致性成本权重和均方差EMA衰减。算法对它们的值有多敏感?我们可以看到,在每种情况下,好的值大约跨越一个数量级,在这些范围之外,其性能会迅速下降。注意,
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[235377],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


