英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
《IEEE控制系统技术汇刊》第21卷第1期.2013年1月1日
制动控制系统的数据驱动设计
Simone Formentin, Pierpaolo De Filippi, Matteo Corno, Mara Tanelli和Sergio M.Savaresi
【摘要】:主动制动控制器在汽车上的应用具有显著的机械差异。低成本的产品要求控制设计的方法,提供方便和快速校准和重新调整能力。使用基于模型的控制方法严重的依赖具体的车辆动力学描述,使得这项任务变得很困难。为了解决这些问题,本文提出了一种主动制动的数据驱动方法控制设计,基于虚拟参考反馈调优(VRFT)方法的补充与数据驱动的非线性补偿器。这个方法的有效性是评估在一个成熟的多体模拟器和a tire-in-the-loop实验装置。
关键字——制动控制、数据驱动控制、智能比例积分导数(PID)、智能pi、双轮车辆,车辆动力学,虚拟参考反馈调谐。
- 介绍和动机
这种防抱死制动系统(ABS)是其中最重要的一种道路车辆主动安全系统,帮助司机保持转向控制和减少紧急制动动作时的停车距离。
在自动制动控制领域,提出了ABS控制策略主要分为两大类:车轮减速和车轮滑动控制器。
车轮减速控制器(见[1]和参考资料其中)是增加或减少的开关系统。根据车轮减速阈值制动压力,从而触发轮滑极限周值与摩擦曲线峰值对应。他们是有效的但需要昂贵的调谐,并不是最佳的,因为振荡行为。另一方面,车轮滑动控制器手,见例[2]-[5],连续调节车轮滑移至期望的目标值。这种方法产生更好的性能,但它需要精确的测量或估计车轮滑动。在[6]中,采用混合滑移-减速(MSD)控制方法提出了哪一种,通过调节凸组合车轮打滑与车轮减速,完美结合车轮减速和车轮打滑控制的特点。
稿件于2010年11月22日收到;2011年5月4日修订;接受2011年8月19日。最终稿于2011年10月7日收到。日期2011年11月4日出版;当前版本的日期为2012年12月14日。由副主编J. Lu推荐。这项工作得到了MIUR Project的部分支持MIUR项目“工业系统识别和自适应控制的新方法”,由奥地利机电一体化能力中心负责(ACCM)。
S. Formentin, P. De Filippi, M. Tanelli, and S. M. Savaresi are with the Di-partimento di Elettronica e Informazione, Politecnico di Milano, 20133 Milano,意大利(电子邮件: formentin@elet.polimi.it; defilippi@elet.polimi.it; tanelli@elet.polimi.it; savaresi@elet.polimi.it)。
M. Corno就职于代尔夫特技术中心系统与控制中心大学,2628光盘代尔夫特,荷兰(电子邮件:m.corno@tudelft.nl)。数字对象标识符10.1109/TCST.2011.2171965
一般情况下,制动动力具有高度的非线性和不确定性;因此,ABS设计人员必须投入大量的资源进行微调。此外,在过去的几年里,ABS系统在mo-torcycle上也变得很常见(参见[3]、[7])。这些车辆具有特殊的运动特性(参见,例如[8],[9]),这些特性可能会呈现测试工程师掌握的技术已经过时。
上述讨论揭示了一种新方法的必要性。对制动控制器的设计能够产生快速的标定和校正
安全。在目前的工作中提供了所需的灵活性,由所谓的直接数据驱动的设计方法(见[10]-[12])。从初步结果开始讨论,在[13]中本文提出了一种节点设计方法,结合虚拟参考反馈调优(VRFT),例如 [11]具有这种类型的数据驱动非线性补偿器,在[14]中提出了一种主动制动控制系统的设计。在此基础上设计了数据驱动控制系统默沙东公司框架。提出的控制方案的性能方法是评估通过一个两轮车辆模拟器(MSC BikeSim)和viaexperimental tests在a tire-in-the-loop设施。
本文的创新贡献在于探索数据驱动设计对制动控制问题的适用性。更具体地说,这项工作将解决以下问题。
- 制动数据驱动控制器设计的适用性控件,这是一个应用程序域,两者都处于建模不足状态测量噪声具有重要意义。
- 本文将VRFT方法与Fliesset al. [14]提出的非线性校正器进行了扩展,展示了重缝设计如何提高VRFT的鲁棒性方法在非线性系统中的应用。在这方面,它还提供了一个全面的复杂性分析。该方法在[14]中的调优阶段及其优缺点在处理低信噪比时会出现什么情况(信噪比)的设置。
该摘要的结构如下。第二节给出了MSD控制的基本原理,而第三节给出了MSD控制的基本原理制动控制的数据驱动设计方法。此外,第四节a节讨论了闭环系统的验证,在两轮车辆模拟器上进行了性能测试,并对控制器的整定阶段进行了讨论具有显著的建模不足和高信噪比。最后,对环中轮胎系统进行闭环验证给出了低信噪比的实验装置在IV-B节中,突出其中出现的调优问题存在明显的测量噪声。
- 混合滑移-减速控制方法
为阐释水务署的管制原理,我们参考以单角模型为出发点,对其进行了研究许多主动制动控制器的设计要点,见[15]及其参考。模型如下所示方程:
(1)
当是纵向滑移 [m/s]车辆的纵向速度,以及 [rad/s]的角度车轮的速度。进一步, [Nm]为制动力矩, [N]为轮胎-路面接触点的垂直力, [kg m], [kg]和 [m]为车轮的转动惯量四分之一车的质量和车轮半径,为描述路面状况的静态函数,见,例子[16]。
MSD方法还利用了归一化线性车轮减速,定义为
(2)
在车轮滑移控制设计中,(参见,例 [2],[6],[15]),接下来我们假设车辆的纵向动力与车轮转动解耦.由于惯性的巨大差异而产生的动力学。因此,第二个忽略系统(1)方程,车速为被认为是一个缓慢变化的参数。这个滑倒动力学是用一阶模型来描述的。
为了展示MSD控制原理,我们需要计算系统的平衡。我们感兴趣的平衡点在制动过程中,其特点是 (即,不断纵向滑动) 这就是常数归一化车轮减速。具体地说。一个是感兴趣的求出相应的稳态正态车轮减速值。通过微分关于时间车轮打滑,. 代入这个表达式,第二个得到系统(1)的方程和(2)的定义的函数表达式,即
(3)
MSD的主要思想是定义一个输出控制变量ε,为组合,即
. (4)
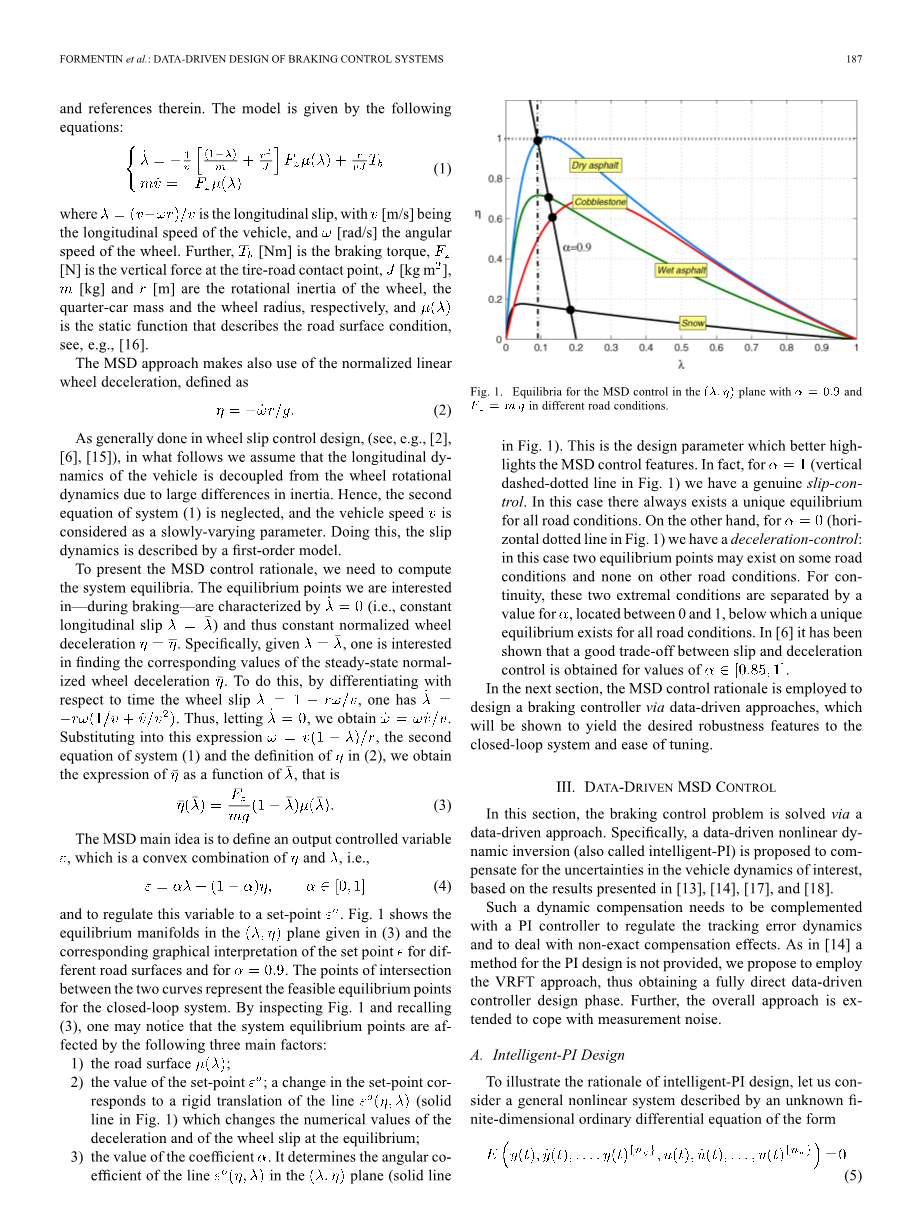
将该变量调节到一个设定值,如图1所示的平面上的平衡流形不同路面设置点()的对应图形解释。交点这两条曲线之间代表可行平衡点.对于闭环系统,通过检查图1和回顾(3)可以看出,系统平衡点受以下三个主要因素的影响:
- 路面;
- 设定值;设置点的变化-响应直线的刚性平移()(实心图1)中改变的数值平衡时的减速和车轮滑移;
- 系数的值。它决定了直线在平面(实线)上的角系数 () ,它决定了直线在平面上的角度共效率(图1中的实线),这是更好地突出MSD控制特性的设计参数。事实上,对于(垂直的图1)中虚线表示的是真正的控制。在这种情况下总是存在唯一的平衡适用于所有道路状况。另一方面,对于 (图1中横截面虚线)我们有加速控制:在这种情况下,某条路上可能存在两个平衡点在其他道路条件下没有。对于连续性,这两个极端条件用隔开值的值,位于0到1之间,在其下面有一个惟一的所有道路条件都存在平衡。在[6]中一直是这样说明滑移和减速之间有很好的平衡的值进行控制。
图1.在不同的路况下,当和的(eta;,lambda;)平面上时MSD控制的平衡点
在下一节中,将使用MSD控制原理设计了一种制动控制器数据驱动的方法,其中会否显示出所需的稳健性特征闭环系统,调优方便。
- MSD数据驱动控制
本节主要解决了制动控制问题数据驱动的方法。具体地说,本文提出了一种基于数据驱动的非线性运动反演方法(也称为智能pi反演)来补偿车辆动力学中的不确定性,根据[13]、[14]、[17]、[18]的结果。
这种动态补偿需要得到补充,采用PI控制器对跟踪误差进行动态调节并处理非精确补偿效应。比如[14]一个PI的设计方法没有提供,我们建议采用VRFT方法,从而获得完全直接的数据驱动控制器设计阶段。此外,还提出了一种处理测量噪声的总体方法。
- 智能pi设计
为了说明智能pi设计的基本原理,让我们考虑一个由未知的常微分方程形式描述的一般非线性系统
(5)
,输出和E是充分平滑函数的自变量。重新调用它,用于制动应用程序,输入信号为,制动力矩为,输出信号为ε(t)。
现在假设可以将(5)表示为显式输出一阶导数的函数,即. 在[14]中阐述的控制策略的主要思想是
用现象学-逻辑学模型近似函数f,也叫ledultraa –localmodel.
(6)
其中是要选择的(非物理)常数参数使得和的大小相等。
根据[14],控制动作基于2不同的条款:前馈补偿条款和PI动作设计用于形状跟踪误差动力学并保证对动态误差的鲁棒性补偿。将跟踪错误定义为,的表达式为
(7)
其中和是PI控制器的比例增益和积分增益。假设系统动力学如式(6)所示,令,得到数据驱动前馈补偿行为。在此条件下求解(6)得到
(8)
其中是参考轨迹的导数,是F(t)在瞬时t时刻的近似值,计算方法为输出信号导数的估计值。如预期,如果非线性动力学的反演是理想的,(8)可以重写,表明PI控制器完全抑制了跟踪误差动力学。然而,由于超局部模型只是真实动力学的一个近似,补偿误差不完全为零,需要额外的控制动作。然而,如果准确地估计输出的导数,则补偿间隙小到足以证明线性误差动力学假设的合理性,见[14]。
在作者看来,这种哲学的一个缺点是没有提供一种适用于PI控制器的设计方法。要遵完成自动化过程。
注III.1:[14]中的方法是数据驱动的动态方法反演,因此他不能应用,如果过程是一个不稳定的零动态,注意在MSD控制临界存在一个下界在(4)中的参数上,对于所有,该方法基于优化,且逐渐稳定,见[6]。此外转移资金线性化连续时间模型的相对导数为零,线性化模型的离散时间版本也是最小相位。
- 全自动数据驱动设计
由于线性误差动力学的假设,附加PI作用可以用文献中可用的任何线性技术来设计(见例[19])。应该注意的是,这种设计方法是基于模型的,即需要一个误差动力学模型。
通过解决问题从一个模型参考角度来看,即通过指定所需的闭环行为,可以使用VRFT方法[11]。
让所描述的线性误差动力学LTI asymp - totically稳定的离散时间系统,所需的是havior的闭环动态表达通过渐近稳定和最小相位定义参考模型(见[20]的讨论如何使用VRFT非最小相位植物)。在制动应用中,线性化控制时间系统的传递函数为最小相位,相对度为零。此外,前馈补偿作用抵消了系统的非线性,使得单角模型可靠,因此采用了最小相位参考模型。大量的验证试验证实了这一假设的正确性。
VRFT综合通过PI控制器C(z;)选择参数向量来解决模型参考问题
的最小值
(9)
不需要假设任何系统模型的知识,只使用一组输入/输出样本
更具体地说,VRFT最小化了成本标准算法[11]
(10)
其中下标L意味着信号与给定数字滤波器预滤器L(z)。注意最小化(10)通常是不一样的(9)最小化。尽管如此,在[11]表明,这两个标准成本是相同的最小值点的附近,如果控制器不是太underparameterized对最优结构,达到完美的匹配,如果L(z)被选中,这样
式中为用于识别目的的输入信号的(已知)功率密度谱。此外,如果控制类是线性参数(如PI, PID),优化是凸的,成本函数(10)有一个唯一的最小值,只要输入u是持续激励的,[21]。
该方法是基于优化的,最终得到的控制器使闭环系统的行为最接近,而不需要与所选的控制器类实现完全匹配。
图2. 闭环控制结构框图
匹配条件的满足一般不能先验确定,需要通过迭代符号来验证。在制动应用中,我们假设智能补偿足够有效,可以通过单转角模型的滑移动力学来描述感兴趣的(补偿的)动力学[第一个方程(1)]。因此,我们让M(z)是一个一阶模型。仿真和实验结果都验证了该方法的有效性。
最后,需要注意的是,所提出的控制技术与adap- tive控制中使用的输入误差控制技术有很多相似之处,如[22],它可以被看作是一种离线应用于控制器的输入误差直接自适应控制技术。根据这一思路,[23]最近提出了VRFT的自适应版本,使用批量输入/输出(I/O)数据来处理时变动态。
在本节的其余部分,将详细讨论智能动作和VRFT合成的联合使用的实现。首先,值得指出的是,由于VRFT控制与识别技术的联系,它本质上是一种离散时间方法。另一方面,由于其自身的非线性发展,上一节提出的动态补偿方案是连续时间的。为了共同描述完整的控
全文共16604字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[1674]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。