
英语原文共 21 页,剩余内容已隐藏,支付完成后下载完整资料
3
不稳定重力流动液压系统
虽然大多数收集系统设计基于稳态液压,但管道的流量本质上是不稳定的。由于以下原因,流量不会保持稳定
条件:
bull;由于家庭和工业昼夜用水模式的负荷变化
bull;潮湿天气下流入和渗入的变化
bull;循环打开和关闭泵
bull;流量调节装置的行为
bull;湿井尾水位的变化
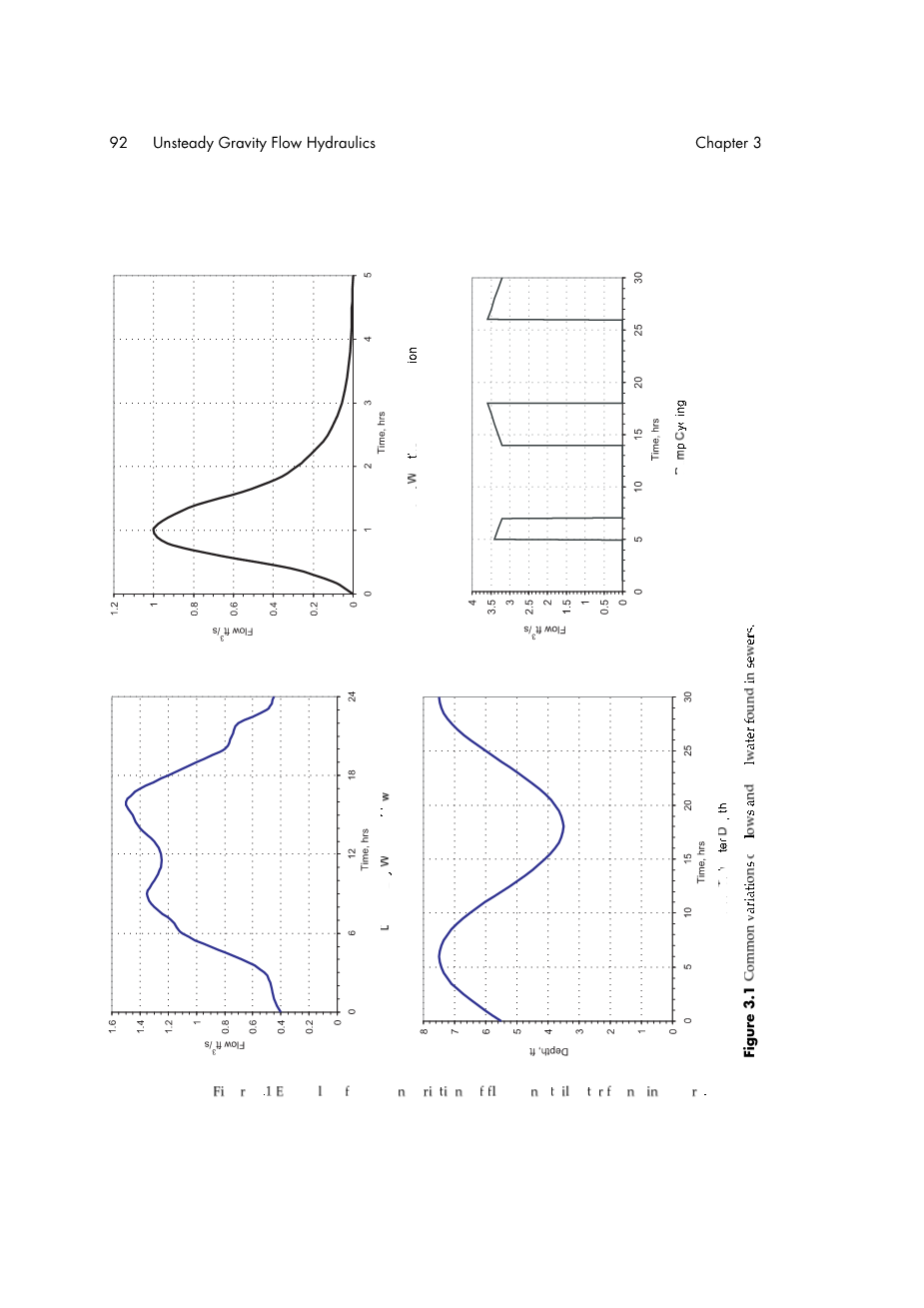
这些时变动态条件如图3.1所示。在分析现有下水道系统的容量限制和溢流情况时,它们尤其重要。与新的土地开发设计污水管道的问题不同,不稳定的水流和溢流成为旧系统的关键问题。泵站的分析也需要量化流量的时间变化。
流量的变化系统逐渐通过收集。随着管道中的流量在上游端增加,水位和流速增加,而后者又向下游流动。另外,流动状态可能会改变。为了应对风暴,合流污水管中的水流开始部分充满,但可能会变成全流量,然后随着尾水在下游端升高或下游限制流量而变得加压。
92 不稳定重力流动液压系统 Chapter 3
图3. 1在下水道中发现的流量和尾水的常见变化。
第3.1节 非稳定流分析的基础93
3.1非稳定流分析的基础
建模通过管道系统的不稳定流动的过程被称为路径流动。国家工程手册(美国土壤保持服务,1972年)将路径定义为:“由存储量,计算上游点洪水到下游点的洪水。”随着来自稳定流动的干扰向下游移动,干扰的峰值趋于平坦化,因为一些水在衰减的过程中进入深度增加。
在稳定流动中,深度和流量之间存在独特的关系(即正常深度,水面平行于通道底部)。这种关系被称为评级曲线。然而,对于不稳定流动,深度偏离正常深度。在增加(上升)流量期间,水面的斜率大于通道底部斜率,并且在递减(下降)流量期间比通道底部斜率更平坦。这导致了一个循环的额定值曲线,如图3.2所示
Discharge, Q
图3.2循环阶段 - 放电曲线示例。
有许多方法可以解决收集系统中的不稳定流动问题,从理论上完成的圣维南方程(3.3节)到简单的水文路径方法(将在后面的章节中介绍)。 用于确定下水道流量的方法已经从为解决河流中的洪水问题而开发的方法演变而来。 但是,由于下水道可能在全管道加压流量和干燥之间转换,因此它们要复杂得多。
本章的其余部分将介绍用于解决非稳态流动问题的方程以及这些方程在实际收集系统中的应用。
94 不稳定重力流动液压系统 第3章
3.2 路径类型
水力模型跟踪通过系统的流量和水力等级,而水文模型跟踪流量并使用简化的近似值来解释动量效应。水文路径方法也被称为集总模型,因为它们计算到达范围的一个位置(下游端)的流量。液压路径模型被称为分布式模型,因为它们同时计算多个横截面的流量(Fread,1993)。
管道中流量的衰减是由于每个管道的临时存储。液压方法在确定储存体积时明确考虑了水的深度。在许多情况下,管道的几何形状非常复杂,以至于确定储存所需的工作量过大,因此储存通过简化的储存方程式近似。水文方法假设知道目前和前一时间步的流入量和前一时间步的流出量足以确定从河段流出。一旦已知流入和流出,可以根据需要使用逐渐变化的流动方法或甚至正常深度来确定水深。
水文路径方法依赖于存储方程,即
(3.1)
Where I= inflow (ft3 /s, m3 /s)
Q= outflow (ft3/s, m3/s)
S= storage (ft3, m3)
已经开发了各种方法来计算流入河流或管道的流出量。 如果下游条件不支持流量,这些方法通常是准确的; 也就是说,如果尾水深度和流量限制不会显着降低下游流量。 当存在下游限制时,水文路径选择方法倾向于预测高于水力模型的峰值,并且因为它们没有充分考虑导致衰减的所有因素而提前到达。
第3.3节 第3.3节 水动力学方程95
3.3流体动力学方程
用于建模下水道非稳定流量的最常用的等式基于流量为一维的假设,压力分布是静水压的,通道的长度远大于深度并且水密度是恒定的。 在这种条件下流体中的扰动被称为浅水或平移波(Linsley,Kohler和Paulhus,1982)。
圣维南方程
下水道中的一维流动最好的属于JeanClaude Barre de St. Venant的方程式来描述。 (它们是三维Navier-Stokes方程的简化)。它们基于这样的假设:横截面中的平均速度足以描述流动,而水面仅在流动方向上倾斜。 圣维南方程包含两个偏微分方程 - 一个用于连续性,另一个用于动量 - 并且有许多不同的形式。 法语(1985)给出了连续性方程
(3.2)
动量方程为
初始条件和边界条件是解决这些方程所必需的。 边界条件通常是出口处的流入水文图和尾水条件,并且初始条件是基于分析开始时的一些预定流量的逐渐变化的流量分布(或正常深度)。
圣维南方程不能解析求解,因此已经开发了各种数值解。 这些方法可以分为有限差分法或特征法。虽然特征方法适用于突变,但对于下水道系统中遇到的流动变化类型,有限差分方法是优选的。
有限差分解决方案将空间和时间划分为一个网格,如图3.3所示,并将近似导数看作有限差分,如
有许多文章描述了解决这些方程的方法,包括Abbott,1979; Chow,1973年; Cunge,Holley和Verwey,1980; Fread,1993; French,1985年;诺阿,2000年; 庞塞,李和西蒙斯,1978年; Price,1973年; Roesner,Aldrich和Dickin
96非定常重力流动液压系统 第3章
图3.3有限差分网格
Son,1989; Yen,1996; 和Yen,2001年。所有讨论应该使用隐式还是显式方法。明确的解决方案更容易编程,但隐含的解决方案往往更加稳定。数值解中使用的点数也影响收敛性和准确性。
特别是,明确的方法需要很小的时间步长(湿天气条件下需要10秒)(Roesner,Aldrich和Dickinson,1989)。 数值稳定性问题可以表现为流动和表面高程的振荡,速度过高或连续性误差。 时间步长的大小应该基于表面波传播管道长度所需的时间,该时间近似为
有限差分方程的成功解决方案取决于时间和距离步长的选择。 较大的步长会导致更快的解决方案,但对于不稳定性和不精确性有更大的潜力。 许多计算机程序是可用的,所以通常不会实施手动计算下水道中的不稳定流量。
流体力学方程的近似值
由于解决Saint-Venant方程的困难,已经开发了大量的近似方法。大多数方法都涉及从动量方程中去除项以提高稳定性。可以重新排列和简化圣维南动量方程以找到放电作为函数 正常流量下的流量和动量方程中的项(Weinmann和Laurenson,1979;法国,1985)。
第3.3节 水动力学方程97
当考虑括号中的所有项时,方程3.6对应于圣维南方程。当括号中的最后一项被忽略时,模型被称为扩散模拟,并且流量不会突然改变,如在上游循环的泵中。仅考虑第一项时,模型仅确定正常深度,称为运动波浪布线。随着每一个越来越接近,方程变得更容易解决,但失去了一些表示真实现象的能力。
在某些情况下(NOAA,2000),建模者已经开发了在特定条件下关闭方程组中的麻烦项的方法,而大多数时候将它们留在解决方案中。
扩散类比
在扩散模拟或扩散波(Ponce,1986)中,连续性和动量方程组合成单一方程
当斜率相对较大且深度较小时,扩散类比效果良好。 系数c通常被称为运动波速度。
运动波
如果在非稳定流动事件期间的条件没有显着偏离正常流量,那么等式3.6右边的大部分项可以被消除以给出
这个方程被称为运动波解。
98非定常重力流体力学 第3章
当流量变化缓慢且阶段放电关系不明显循环时,运动波路径工作良好。
Muskingum路径
一种常用的水文路径是马斯金格姆方法,它假设在一个范围内的存储是由给定的
对于大多数溪流来说,X大约为0.2,而K是河段行程时间的近似值。 在Linsley,Kohler和Paulhus(1982)中给出了基于现场数据确定X和K的图形方法。 一般来说,运动波方法背后的理论使得它更适合于没有顶部而不是下水道的明渠,Samani和Jebelifard(2003)已经表明,如果有一些修改,它可以应用于圆形管道。
距离的排放由下式给出
其中下标指时间步骤1和2一个时间步骤的持续时间为t。 系数由下式给出
Muskingum Routing的典型水文图如图3.4所示。
Muskingum-Cunge路径
Musungeum-Cunge方法是Cunge(1969)提出的Muskingum方法的一种变体,它允许路线系数根据顶部宽度和流量的变化而改变。 它将运动波方法的理想特性与Muskingum方法的优点相结合,因为它允许有限的衰减量。 Ponce,Li和Simons(1978),HEC(1990)和Yen(2001)讨论了这种路径方法。 这在管道流动问题中是特别理想的
第3.3 节水动力学方程99
图3.4流体路径示例。
流量在一定范围内随流量变化剧烈。 Muskingum-Cunge方法的流体力学方程的简化形式由下式给出
100非定常重力流动液压系统 第3章
系数a由下式给出
凸面路径
水文路线的另一个变化是凸面路线,它只使用前一时间步的流量来确定河段的流出量(美国土壤保持服务,1972)。 流量方程是
凸出的路径系数与波速c不同(公式3.8)。 它是到达时间步长与旅行时间的比率。 时间步长应小于行程时间(即c lt;1)。 然而,旅行时间并不是一个常数,而是速度的函数。 它通常被确定为对应于最大流量的50到75%的速度。 系数由下式给出
加权平移路径
虽然旅行时间一般应大于时间步长,但有时候会有一些非常短的管道,这会迫使时间步骤变得不切实际。 对于这样的情况,当需要有一个在cgt; 1时有效的方法时,可以用下式计算放电量
在具有陡坡的小型系统中,扰动基本上沿着管道向下滑动,几乎没有衰减。 为了确定给定时间的流量,只需要在VM的前一个时间步骤的上游查看流量。 该值很可能不在流量已知点之间的某个位置。 因此,需要插值来确定流向下游的流量。
水平池路径
水平池路径(有时称为改性普尔斯)不是管路径的方法,但以路线的方法流经储存池或贮存器。 在下水道流量中,这可以应用于存储潮湿天气流量的盆地。 这种方法适用于对头部损失几乎不如存储容量重要的建模要素。
第三节 路径方法的复杂性101
方法摘要
表3.1总结了用于近似全动力学方程的方法,该方法基于Haestad Methods等人的类似表格。(2003年)。 该表格列出了简化中适用的假设。
一般来说,只要收集系统没有备份和流量反转,对圣维南方程的大多数简化可用于废水收集系统。 在这种情况下,需要完整的圣维南方程。 然而,在设计情况下,工程师不会建造污水管以便回流和逆流,所以简化的路径方法可以正常工作。 在小型系统中,不需要简单的路径方法,因为稳定的峰值流量分析通常是足够的。
3.4 路径方法的复杂性
虽然上一节讨论的方法可以解决渠道和管道流量不稳定的问题,但真正的废水收集系统可能包含这些方法没有考虑到的并发症。
本节讨论的每一个复杂情况都需要对流路径进行调整。 调整取决于正在使用的路径方法。
Weigh
全文共13683字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[14981],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


