
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
附录A:外文翻译及原文
翻译
带有屈曲约束支撑的低层钢框架的抗震设计
1.介绍
传统的地震设计思想依赖于结构构件的非弹性变形来耗散输入地震能量。这一设计理念可以为抗震设计提供安全、经济的保障,但不能防止地震对结构的破坏。主要结构构件的损伤可以通过连接梁和柱与铰链,使用抗侧荷载构件来承受侧立地震荷载[1]来防止或减小。在这种所谓的耐久支撑框架(DTBF)中,地震引起的大部分能量耗散和结构破坏将集中在抗侧荷载构件上,主要构件将保持弹性。地震后,损坏的抗侧载构件可以在合理的成本下轻易更换。
一般情况下,钢支撑被用作为钢结构提供侧向刚度的经济手段。
然而,钢支撑结构在地震荷载作用下的能量耗散能力受到支架屈曲的限制。这就是为什么大多数抗震设计规定对加固框架的响应修正系数要比矩框架的响应修正系数更低。采用带扣支撑(BRBs)可大大提高钢框架结构的能量耗散或损伤预防能力。它们通常由能够承受明显非弹性变形的钢芯和能够抑制核心元件整体和局部屈曲的套管组成。根据前人的研究[2-5],BRB表现出稳定的滞回行为,具有较高的能量耗散能力。BRBs的使用大大提高了结构的耗能能力,降低了主要结构构件的非弹性变形需求。
研究了直接位移设计方法[6]在DTBF结构上的适用性。设计过程首先应用于单自由度(SDOF)系统,并进一步扩展到三层和五层结构以验证该方法的适用性。BRBs设计用于抵抗侧向荷载,使最大顶板位移与给定的目标位移一致。与支柱相连的梁和柱是为重力载荷加上从支架上转移的地震载荷而设计的,这样它们在地震中保持弹性。两个人工地震记录来自基于UBC 97的设计谱,使用记录构建的响应谱进行设计。进行了时间-历史分析,以确定最大位移是否与目标位移一致。
2.设计SDOF系统的过程
2.1.设计过程
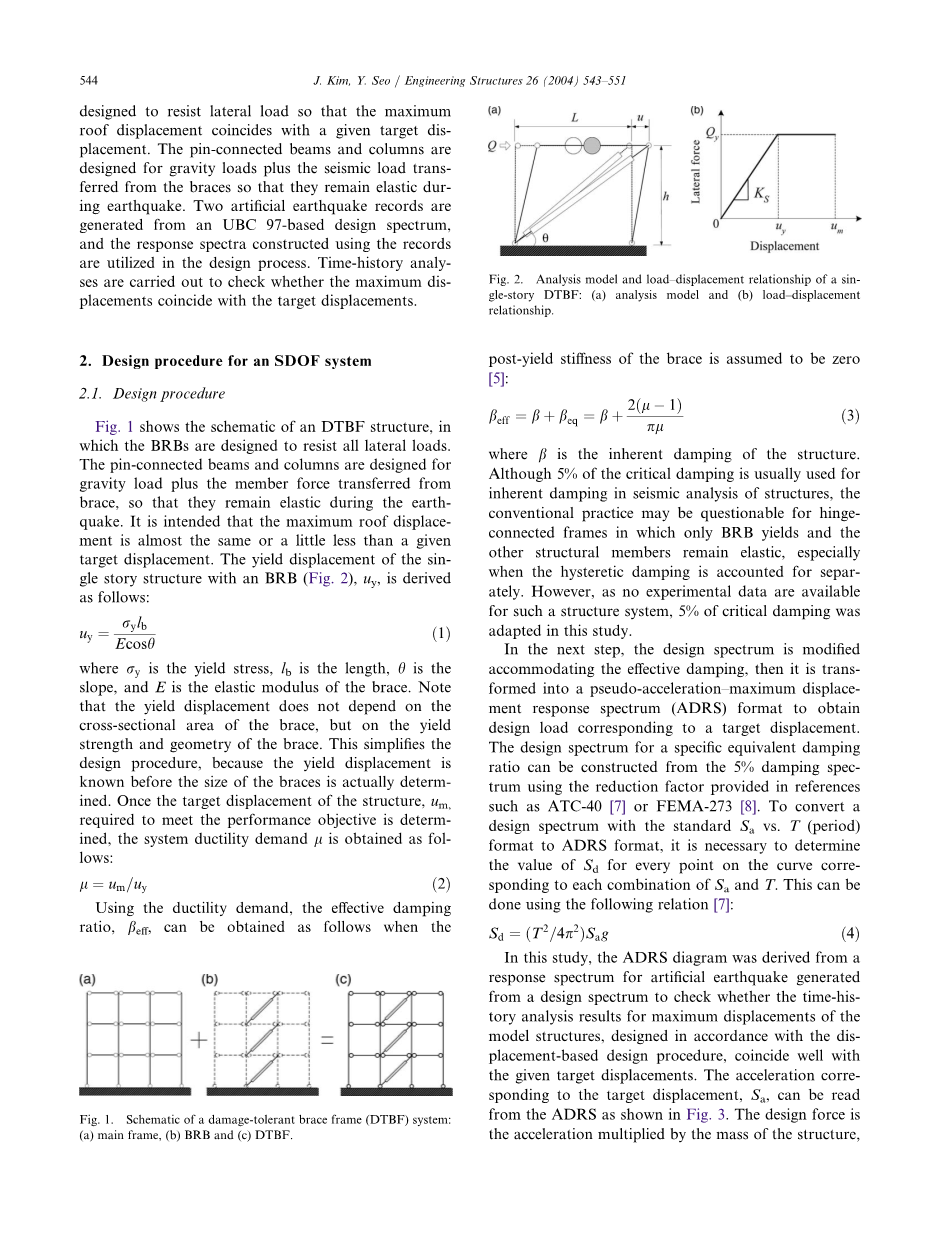
图1显示了DTBF结构的示意图,其中brb被设计用来抵抗所有的横向载荷。与支柱相连的梁和柱是为重力载荷加上从支柱转移的力而设计的,因此它们在地震中保持弹性。其目的是使顶板的最大位移几乎等于或略小于给定的目标位移。用BRB(图2)uy计算单层结构的屈服位移,得到如下:
式中为屈服应力, 为长度, 为斜率,E为支撑的弹性模量。注意,屈服位移不取决于支撑的横截面积,而是取决于支撑的屈服强度和几何形状。这简化了设计过程,因为在确定支架尺寸之前,已经知道了屈服位移。一旦确定了结构的目标位移,嗯,满足性能目标,系统的延性需求mu;得到如下:
当假定支撑的屈服后刚度为零时,利用延性需求,即有效阻尼比,可以得到如下结果
图1所示 耐损伤支撑架(DTBF)系统原理图:(a)主框架,(b) BRB和(c) DTBF
图2所示 单层DTBF的分析模型和荷载-位移关系:(a)分析模型和(b)荷载-位移关系。
其中beta;为结构的固有阻尼。虽然5%的临界阻尼通常用于结构的地震分析中固有的阻尼,但是传统的做法对于只有BRB屈服和其他结构构件保持弹性的铰链连接框架可能是有问题的,特别是当滞后阻尼单独考虑时。然而,由于这种结构系统没有实验数据,因此在本研究中采用了5%的临界阻尼。
在下一步中,对设计谱进行修改以适应有效阻尼,然后将设计谱转化为伪加速-最大位移响应谱(ADRS)格式,得到目标位移对应的设计荷载。特定等效阻尼比的设计谱可以使用参考文献中提供的还原因子,如ATC-40[7]或FEMA-273[8],从5%的阻尼谱中构建。要将设计谱与标准 vs. T (period)格式转换为ADRS格式,需要确定曲线上每一点对应的与T和T组合对应的值:
在本研究中,ADRS图是从一个设计谱中产生的人为地震反应谱推导出来的,以检验模型结构的最大位移的时间-历史分析结果是否与给定的目标位移吻合良好。加速度对应于目标位移Sa,可以从ADRS读出,如图3所示。设计力是加速度乘以结构的质量,
图3所示。最大加速度响应的估计
m,如下:
BRB的横截面面积,Ab,满足a的目标性能点。
给定地震荷载确定如下:
该系统的横向刚度,是由横截面积和支撑长度的函数得到的:,
图2(b)描述了BRB的后屈服刚度为0时系统的力-位移关系。
2.2.SDOF系统的数值例子
图4所示。用于分析和设计的地震荷载:(a)设计谱和基于人工记录和(b)人工地震记录的时间历史构造的响应谱。
上述设计过程应用于图2(a)所示的SDOF系统。以下属性被分配到结构:重量=100 kN,故事高度h=4.0米,宽度L=6.0 m,列=h 250times;250times;9times;14(mm),梁=H 420times;200times;8times;13,和弹性模量Efrac14;=210 GPa。支架的屈服应力假设为100 MPa。低强度钢,目前在日本作为一种有效的材料,用于研究,使BRB在其他构件保持弹性的情况下开始屈服。假定支撑显示了完全弹性的塑性行为。梁与柱销相连,柱销与基座相连,横向荷载主要由支撑起抵抗。利用地震系数Ca=0.44、Cv=0.74的设计谱图4(a)生成地震时程记录[9]。在韩国[10]地震事件2400年回程期的设计谱是推荐的。人工记录的时间历史被绘制在时间历史记录中,如图4(a)所示。
通过虚线曲线,并用于设计过程中。第一步,目标位移设为结构高度的1.5%,即6cm。由式(1)得到的屈服位移为0.41 cm,当结构向目标位移变形时,延性比为14.6 cm。在延性比下,有效阻尼比为0.687。在考虑有效阻尼的基础上,对响应谱进行了修正,并将响应谱转化为加速度-位移图。在图中,与目标位移对应的加速度响应为0.17g,通过将结构质量乘以加速度响应得到16.7 kN的屈服力。最后,用式(5)作为2.0 cm2计算支撑所需的截面面积。采用非线性分析程序dep - 2d [11]对结构进行分析。利用人工地震记录的时间-历史分析得出的结构的最大位移为5.7 cm,与6.0 cm的目标位移相当接近。
3.应用多层结构
利用等效SDOF系统推导多层结构的结构响应和设计力是非线性静力分析和设计方法的关键步骤,如容量谱法或直接基于位移的设计。然而,非线性静态过程在应用上有其固有的局限性。Krawinkler[12]指出,没有物理原理可以证明滞回能量耗散与等效粘性阻尼之间存在稳定的关系,特别是对于高度非弹性系统。Fajfar[13]指出,推覆分析是基于一个非常限制性的假设,即一个独立于时间的非定置形状,它在原则上是不准确的,对于那些具有更高模式效应的结构来说。然而,非线性静态过程被认为是非线性动力方法的有力替代,特别是在常规、低层结构的初步分析和设计阶段,因为它们在概念上的简单性和应用上的便利性。
3.1.设计目标
在多层结构中,给定地震荷载的地震设计目标为:(i)最大位移等于目标位移;所有故事的最大层间漂移是相同的;(三)在推覆分析中,所有故事的大括号同时产生;(四)支撑单元横截面面积各层耗能相同。在设计目标中,第三个目标可以很容易地实现,如果每个层中支撑的大小与地震层对结构施加的静力成正比。图5(a)为地震层力分布,随高度线性增加,对应层位移。图5(b)给出了多层耐受损伤结构的层间剪切-层间位移关系(推覆曲线),其中安装了零后屈服刚度的支架。如果背带按照建议的程序设计,则每个层的屈服位移是相同的。在这种情况下,可以预期地震造成的结构破坏在整个故事中是均匀分布的。
图5所示 DTBF的目标变形形状和推覆曲线:(a)目标变形形态;(b)层间剪切与层间离散。
3.2.设计过程
在前一章中提出的SDOF结构的设计过程可以进一步扩展到如下的多层结构。
1.最大位移量的计算。
如果故事的高度和背带的屈服强度
在整个结构中都是一样的,在屈服点的最大位移,是层的屈服位移,Eq.(1),乘以层数n:
2.延性需求的计算。
通过将给定的目标顶板层位移与屈服位移(Eq.(2))分割得到延性需求。
3.转换为等价的SDOF系统。
多层结构需要转换为等效的SDOF结构来获得设计负载。等效SDOF系统的屈服位移和最大位移如下[8]:
基本模态的模态参与因子 ,可以得到为
其中为第j层的质量,为基本模态形状矢量的第j个分量。在本研究中,模式形状假设为一条直线,如下所示:
n是故事的个数。在下面的章节中,我们说明了按照预先提出的方法设计的低阶DTBF结构的基本模态形状接近于直线。然而,随着故事数量的增加,由于列的变形性,线性模式的假设被违背。
4.从加速度-位移图中估计有效阻尼(Eq.(3))和确定加速度响应。
5.计算的设计力量。
原多层结构的设计基底剪力可通过将上一步得到的等效SDOF结构的加速度响应乘以基模有效质量得到:
有效模态质量Mm可得:
A1是第一层支柱的横截面面积。考虑到较高的模态效应,第xx层的地震层力需要确定。在本研究中,使用韩国地震设计规范[14]的下式来分布整个楼层的基底剪力:
4.数值例子
4.1.模型结构和地震记录
如图6所示,将上述设计过程应用于3- 5层结构。设计了铰链连接的梁和柱,使其在重力和横向地震荷载作用下保持弹性。结构的层重为100kn。所选成员以朝鲜语发言标准(KS),如表1所示
之前用于分析SDOF系统的地震记录(图4(b))再次用于验证设计的有效性(此记录被命名为eq1)。另一个人工记录(EQ-2)也是基于相同的设计谱生成的,使用时程记录EQ-2构造的响应谱与设计谱吻合得很好。
图6所示。应用建议设计程序的模型结构:(a)三层结构和(b)五层结构。
表1:模型结构构件尺寸(单位:mm
|
Story |
Columns |
Beams |
|
(a) 3-Story |
||
|
1–2 3 |
H 250 times; 250 times; 9 times; 14 H 200 times; 200 times; 8 times; 12 |
H 400 times; 200 times; 8 times; 13 |
|
(b) 5-Story |
||
|
1–3 4–5 |
H 300 times; 300 times; 10 times; 15 H 250 times; 250 times; 9 times; 14 |
H 400 times; 200 times; 8 times; 13 |
4.2.箍筋的设计
满足给定设计目标所需的BRBs的横截面面积是针对四个目标顶层位移确定的:1.0% (Case A)、1.5% (Case B)、2% (Case C)和2.5% (Case D)。利用人工记录eq1和EQ-2构造的响应谱来设计支架。在表2中给出了与eq1对应的响应谱设计的大括号的大小,并在表3中给出了为四个目标位移设计的结构的基本周期。从表中可以看出,钉连接梁柱节点支撑框架的自然周期一般比刚性框架的周期长。
4.3.推覆曲线和模式形状
图7描述了为eq1设计的5层模型结构的俯仰曲线,目标位移为建筑物高度的1.0% (Case A)。可以看出,5层结构的层间位移在每个层上都是相同的,符合设计的意图。图8所示为案例a所设计的模型结构的模态,可以观察到3- 5层结构的模式形状接近直线。
表2支架横截面面积(单位:cm^2)
表3:各种目标位移设计的模型结构的基本周期
|
Model structure |
Case A |
Case B |
Case C |
Case D |
|
3-Story |
0.83 |
1.15 |
1.21 |
1.27 |
|
5-Story |
1.10 |
1.33 |
1.52 |
1.72 |
图7所示。五层模型结构的层力-层位移关系。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[467661],资料为PDF文档或Word文档,PDF文档可免费转换为Word


