荷载路径对FRP混凝土性能的影响外文翻译资料

 2022-04-19 06:04

英语原文共 16 页，剩余内容已隐藏，支付完成后下载完整资料

荷载路径对FRP混凝土性能的影响

摘要：本文介绍了一种在纤维增强聚合物（FRP）约束下承受恒定轴向荷载和增加弯矩的混凝土圆柱的实验研究。 共测试了55个圆柱体，其中FRP厚度和轴力比是变量。与另一载荷偏心和增加轴向载荷的载荷路径相比，该载荷作用下的圆柱体的反应截然不同。 结果表明：荷载路径对FRP约束混凝土的应力 - 应变行为有显着影响，不同荷载路径下FRP约束混凝土需要不同的应力 - 应变模型。 根据试验结果，提出了FRP约束混凝土在相关荷载路径下的应力 - 应变模型。DOI: 10.1061/(ASCE)CC.1943-5614.0000799. copy; 2017 American Society of Civil Engineers.

关键词：混凝土; 柱; 应力 - 应变模型; 加载路径;约束; 纤维增强聚合物（FRP）。

介绍

由于纤维增强聚合物（FRP）在提高构件的强度和延展性方面具有很高的效率，因此它已成为加固，改造和修复钢筋混凝土柱的通用方法。关于轴心轴向载荷作用下的FRP加固混凝土的文献报道了进行了大量的研究。然而，关于承受轴向载荷和弯矩或偏心载荷的FRP夹层混凝土柱的知识要少得多。基于现有知识和最新发现，FRP约束混凝土柱在轴心受载和弯矩共同作用下的性能与轴心轴向受力下的情况有显着差异。为轴心荷载柱研究出的应力应变模型不适用于偏心荷载柱。换句话说，FRP约束混凝土柱的应力 - 应变特性与加载路径有关。已经进行了实验研究来研究RC柱的载荷路径依赖性（没有外部夹套）；Bousias等人（1992）研究了恒定轴向载荷下8根双轴加载路径下钢筋混凝土柱的受力状态；Qiu等人（2002）研究了载荷在七条载荷路径下的钢筋混凝土柱承载能力； Rodrigues等（2015）研究了六种水平荷载下不同轴向荷载下的钢筋混凝土柱。实验结果表明，荷载路径对钢筋混凝土柱的非线性行为，延性和承载能力有显著影响。

关于FRP约束混凝土柱的荷载路径依赖性的报告很少。 Wu和Jiang以前开发了具有恒定偏心率和增加轴向力的FRP约束混凝土柱的应力 - 应变模型（2013b）。 然而，该模型是否适用于其他载荷路径下的偏心受压混凝土柱（如恒定的轴向载荷下偏心率增加）。本研究的目的是研究FRP约束混凝土柱的应力 - 应变行为的载荷路径依赖性。

试验计划

这项工作共测试了55个圆柱体。 测试变量为FRP厚度，混凝土等级和轴向力。 所有试件都在恒定的轴向力和逐渐增加的弯矩下进行试验。 记录包括弯矩曲率曲线和FRP护套侧向应变的响应。从试验结果中获得了力矩与轴向力的关系（M-N相互作用图）。测试数据也可用于开发这种加载方案下FRP约束混凝土的应力 - 应变模型。

样本设计

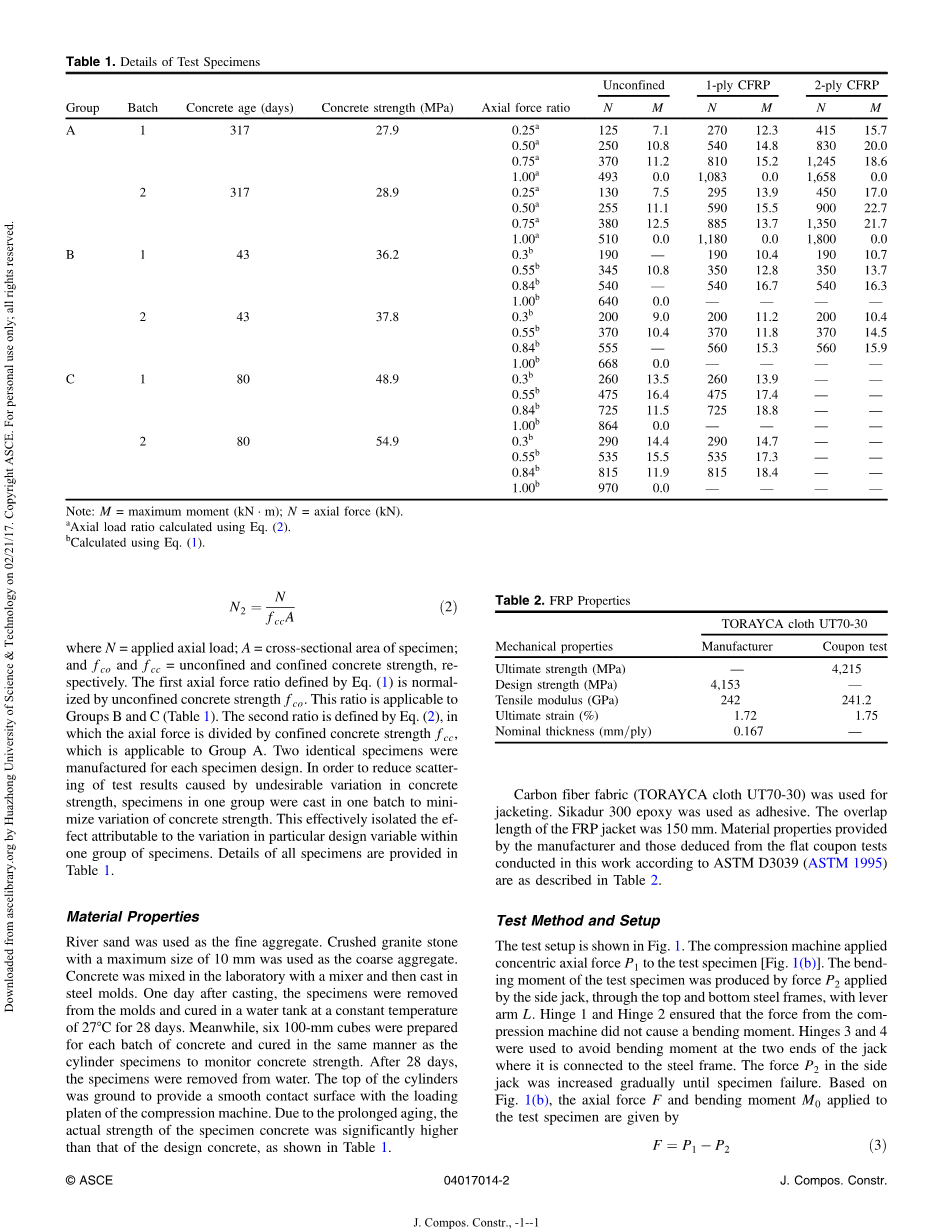
测试样品的直径为150毫米，高度为300毫米。护套厚度有三种变化：0层，1层和2层碳纤维增强塑料（CFRP）。A组，B组和C组分别使用C20，C30和C40三种混凝土等级。试验中涉及8种不同的轴向力值（表1）。 对于不同组的样本定义了两个轴向力比:

(1)

(2)

其中N =施加的轴向载荷; A=试样的横截面积;fco和fcc分别为无约束混凝土强度。第一轴力比由公式（1）用无侧限混凝土强度fco标准化。 该比率适用于B组和C组（表1）。第二个比率由公式（2）定义，其中轴向力除以受限混凝土强度fcc，这适用于A组。两个相同的试样制造每个样本设计。 为了减少因混凝土强度发生不希望有的变化而导致的试验结果的散射，一组试件被浇铸成一批，以减少混凝土强度的变化。 这有效地隔离了一组样本内由于特定设计变量的变化而导致的效应。表1提供了所有样本的细节。

材料特性

河沙被用作细骨料。使用最大尺寸为10mm的碎花岗岩石作为粗骨料。将混凝土在实验室中用混合器混合，然后浇铸在钢模中。铸造后一天，将样品从模具中取出并在27℃的恒温水箱中固化28天。同时，为每批混凝土准备六个100毫米立方体，并以与圆筒试样相同的方式固化，以监测混凝土强度。 28天后，将标本从水中移出。 研磨圆柱体的顶部以提供与压缩机的加载台平滑的接触表面。 由于老化时间的延长，试件混凝土的实际强度显着高于设计混凝土的强度，如表1所示。

碳纤维织物（TORAYCA cloth UT70-30）用于护套。Sikadur 300环氧树脂被用作粘合剂。FRP护套的重叠长度为150毫米。由制造商提供的材料特性以及根据ASTM D3039（ASTM 1995）在本工作中进行的平板试样测试所推导出的材料特性如表2所述。

测试方法和设置

试验装置如图1所示。压缩机对试样施加轴心轴向力P1[图1（b）]。 测试样品的弯曲力矩是通过侧面千斤顶通过顶部和底部钢框架施加的力P2产生的，杠杆臂L是铰链1和铰链2，确保来自压缩机的力不会导致弯曲时刻。使用铰链3和4来避免千斤顶连接到钢框架的两端的弯曲力矩。侧千斤顶中的力P 2逐渐增加直至试样失效。根据图1（b），施加在试样上的轴向力F和弯矩M0由下式给出:

(3)

(4)

其中L =从P2到P1的距离，如图1（b）所示。在试验开始时，预先设计的轴向力F首先通过P 1施加,P2 = 0,然后力P2逐渐增加。为了在测试期间保持恒定的轴向力F，根据P 2的读数，P 1也被手动增加，使得P1 -P2 =恒定。 以这种方式，试样在恒定的轴向力和增加的弯曲力矩下进行试验直至失效。

仪表

轴向载荷P1由压缩机的内部测力传感器测量,用另一个称重传感器测量载荷P2（图1）。数字图像相关（DIC）是一种可在测试过程中连续捕获位移和应变场的光学测量技术，用于捕捉测试样本的极端压缩面（最大压缩面）上的面部变形。图2（a）]。 DIC系统已被证明是非常有效和准确的，用于在各种类型的实验工作中连续测量试样表面应变场（Yun and Wu 2011; Wu and Jiang 2013a; Jiang et al。2014; Wu et al。2015;Wu和Jiang2013c）。其他七个应变计（＃2至＃8）用于测量图2（a）所示位置处的横向应变。四个长度为180mm的LVDT用于测量试样的轴向变形和弯曲，其中两个安装在最小压缩侧，另外两个安装在最大压缩侧[图2（b）]。从LVDT到试样最外层纤维的距离为11.5 mm [图2（b）]。通过LVDT和DIC同时测量样品的最大压缩侧上的垂直应变，并且通过LVDT监测最小压缩侧上的垂直应变。在测试过程中，所有的测量都通过自动数据采集系统进行记录。

测试过程

样本测试使用以下步骤中的步骤：

  1. 将样品固定在带有四个LVDT的铝框架中[图2（b）];
  2. 将力P 1施加到普通混凝土试件的承载能力的约30％。 施加力矩的顶部和底部钢框架保持水平[图1. 1（a）]，P 2 = 0;
  3. 调整试样的位置，使四个LVDT的读数相同（差值lt;10％）。 在这种情况下，样本被认为是在P1;
  4. 下轴心加载的。 将压缩机的压缩力P 1改为其设计的轴向力F（表1）。 通过增加P2的位移（每次约2.5毫米）应用小的增量曲率;
  5. 读取P2的值并将压缩载荷增加到P1=F P2，以保持恒定的轴向力;
  6. 转到步骤5为P2应用另一个增量位移并重复此过程，直到试样失效。

实验结果和讨论

破坏模型

具有不同轴向力比的所有试件的典型失效模式如图1和图2所示。 A组如图3.（a-c）所示， B和C组如图3.（d-f）所示。B组和C组试样的损伤程度（混凝土破碎程度和FRP破裂程度）一般小于A组试样，因为其轴向力较小。 对于轴力比最小为N1 = 0.3的试件，试件的张力侧出现横向拉伸裂纹，随着弯矩的增加，试件的张力侧进一步扩大，玻璃钢夹套的断裂主要在最大压缩侧附近。 对于具有较高轴力比N1 = 0.55和0.84的试件，FRP和混凝土破坏区的尺寸随着轴向力的增加而增加[图3（e和f）]。

载荷 - 变形曲线

对于典型的试样，矩形与LVDT位移曲线如图4所示。每个试样有两条曲线，一条来自最大压缩侧的两个LVDT的平均读数，另一条来自最小压缩侧。压缩位移是正的，拉伸是负的。 LVDT的位置如图2（b）所示。对于组A中N 2 = 0.25和0.5的轴向力比值相对较小的试样[ 图4（a和b）]，弯曲力矩达到峰值后会稍微下降。峰值时刻附近有一个屈服平台，随着轴力比的增加平台的程度减小。对于轴力比为N2 = 0.75的试件，屈服平台几乎不存在，弯矩在达到峰值后迅速下降。与A组标本相比，B组和C组标本[图.4（c-e）]在最终失效之前通常具有较大的变形，这明显是由这两组中较小的轴向力造成的。从曲线中还可以看出，轴向力对FRP护套的厚度有更显着的影响。表1总结了所有试样的峰值弯矩和轴向力。

曲率和应变的计算

试样变形如图5所示，变量S1和S2分别是顶部和底部框架之间试样的最小压缩侧和最大压缩侧的长度。测试前顶部和底部框架之间的原始距离为180毫米。因此，LVDT的标距长度为H = 180 mm， 其他尺寸如图5所示。如果最小和最大压缩侧的LVDT分别给出Delta;L1和Delta;L2的读数，则这两个LVDT位置处的长度分别为L1 = H-Delta;L1和L2 = H-Delta;L2。根据图5中的几何关系，可以得到以下关系式：

(5)

可得：

(6)

另外：

(7)

变量S1和S2可以用来计算：

(8)

(9)

试样的最小和最大压缩侧的应变ε1和ε2分别由下式给出:

(10)

(11)

样本的曲率可以通过计算:

(12)

  1. N互动图表

实验图表

用于柱设计的常规M-N相互作用图可以通过从对应于特定轴向力N的图6中的曲线找到最大力矩阻力M来获得。生成并示出了所有类型的试样的M-N相互作用图 （1）试样在轴心荷载作用下的轴向承载能力（M = 0）；（2）在A组成员的轴力比为N2 = 0.25,0.5和0.75时的曲线上的三个点，或在B组和C组中的N1 = 0.3,0.55和0.84; （3）N = 0处的纯弯矩。

对于M = 0的第一点，只有A组成员进行了受限混凝土强度fcc的测试。 因此，第一点的实验结果仅适用于A组成员。对于B组和C组的标本，这一点是根据Wei和Wu（2012）的约束混凝土理论模型计算得出的。对于N=0的最后一点，如果忽略拉伸阻力，M就是零。 根据CEB-FIP编码（1993）的拉伸应力 - 应变模型，图7中N=0处的力矩阻力非常接近零。 第一个和最后一个点之间的其他三个点是从测试曲线获得的，如图6所示。

理论图表和讨论

当应力应变模型可用时，M-N相互作用图可以由横截面分析产生。这两种载荷情况下的应力 - 应变曲线用于产生M-N图表：（1）在轴心载荷下；（2）偏心加载时偏心率恒定，轴向力增大。轴心加载的应力 - 应变曲线可直接从测试结果中获得，而无需使用模型。在轴心加载下测试的轴向应力 - 应变曲线如图8所示。然而，只有A组试样在轴心加载下测试到FRP破裂。当没有实验应力 - 应变曲线时，采用Wei和Wu（2012）开发的适用于轴心圆柱的应力 - 应变模型。对于第二种情况，由Wu和Jiang（2013b）提出的应力 - 应变模型，由具有恒定偏心率的偏心加载柱发展而来，用于产生M-N相互作用图。由于篇幅限制，省略了使用上述应力 - 应变模型计算M-N相互作用图的详细程序。

从图4可以看出。从图7（a和b）可以看出，对于一定的轴向力，A组试样的所有试验力矩值均小于Wu和Jiang模型计算得到的值，但可以大于或小于应力 - 应变曲线计算值 在轴心加载下。对于B组和C组标本，如图1和图2所示。 图

全文共10359字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[13556]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章