英语原文共 18 页,剩余内容已隐藏,支付完成后下载完整资料
组合结构的模拟与分析
F.H.WITTMANN,P.E.ROELFSTRA 和H.SADOUKI
建筑材料科学实验室,洛桑瑞士联邦理工学院
(1984.2.13收稿)
摘要
首先,我们知道天然磨圆骨料的几何形状可以通过合适的形态学法则进行模拟。任意的组合结构可以通过计算机生成的颗粒得到。任何颗粒的粒径分布都可以考虑在内。通过分析三维组合结构大量的随机截面可以得到一个二维的累积的粒径分布。对截面的分析可以进一步用于研究组合材料(例如混凝土)中表面层的具体性能。用有限元网格划分生成的组合结构后可以进行详细的数值分析。这个方法有两种潜在的应用:(1)骨料模量对组合结构有效模量的影响;(2)骨料浓度对材料(例如混凝土)中水蒸气扩散系数的影响。文章还会简要叙述此方法的进一步发展和可能存在的限制。
- 介绍
混凝土的性能非常复杂,许多细节仍然未被完全研究。然而,结构工程学需要简单可靠的材料定义。很明显,仅仅基于实验方法的研究进程会减缓。先进的数值方法可以提供一个有效的附加工具帮助进行材料研究。
借助模拟方法。复杂的过程例如混凝土腐蚀都可以被更真实地模拟出来。有限元方法可以用于分析组合结构的性能和过程。为了利用这些可能性,所生成的组合结构必须非常接近真实的混凝土。
这篇文章将描述怎样模拟天然混凝土和组合结构的随机几何形状。结构模型的可行性将用一些例子进行验证。
- 天然骨料几何形状的分析与模拟
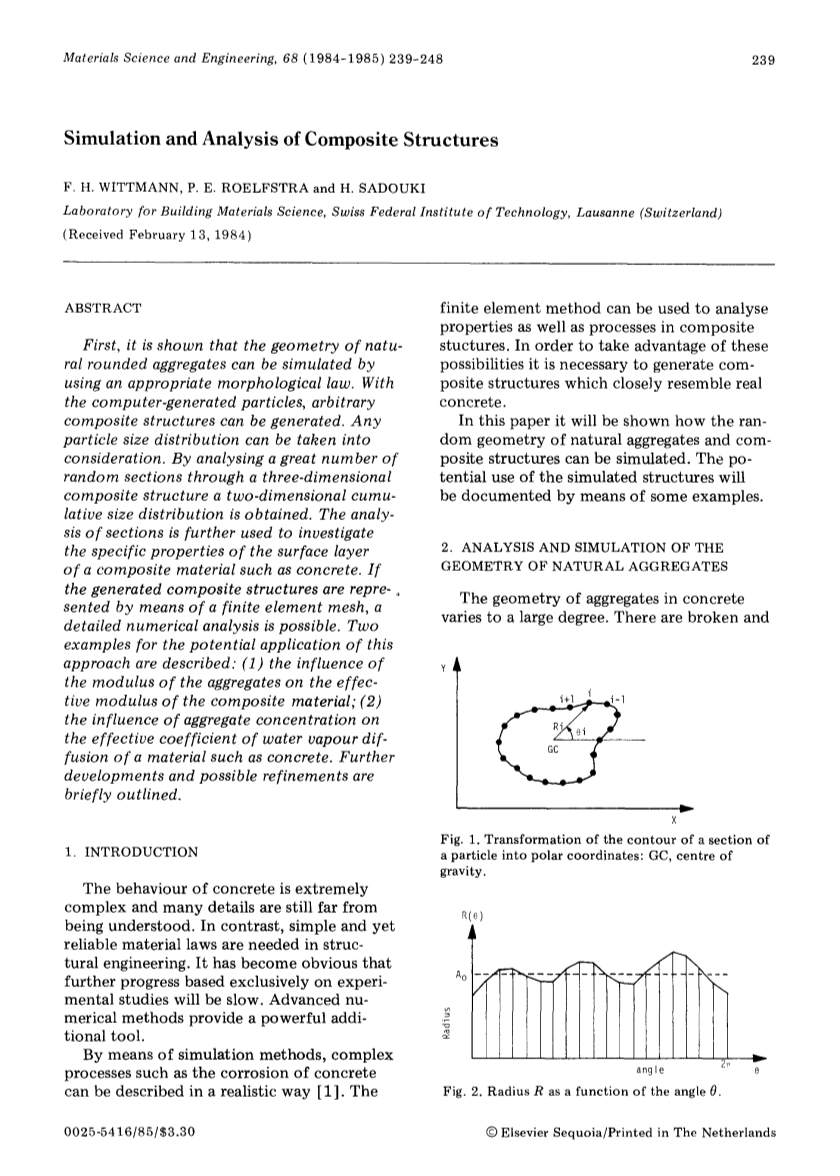
混凝土中骨料的几何形状有很大的变化。有一个破碎的天然磨圆骨料。几何形状的许多尝试,在混凝土学的许多编码中,形状系数会被介绍。为了能够模拟真实骨料的几何形状,会使用更多改进方法。Beddow和Meloy提出了一个分析和描述颗粒的方法。分析一个给定骨料颗粒的截面的可行方法是将轮廓转换成极坐标。如图1所示。极坐标的原点位于截面的重心。现在我们得到一个半径R关于角度theta;的函数。如图2所示生成了一个任意的选中的模型,其结果得到了一个特定截面频率分布:
(1)
在这个方程中,A0是截面的平均半径,Ai是傅里叶频率的振幅,是对应的相位。
图1 将骨料颗粒截面轮廓转换成极坐标:GC是重心。
图2 半径R关于角度theta;的函数
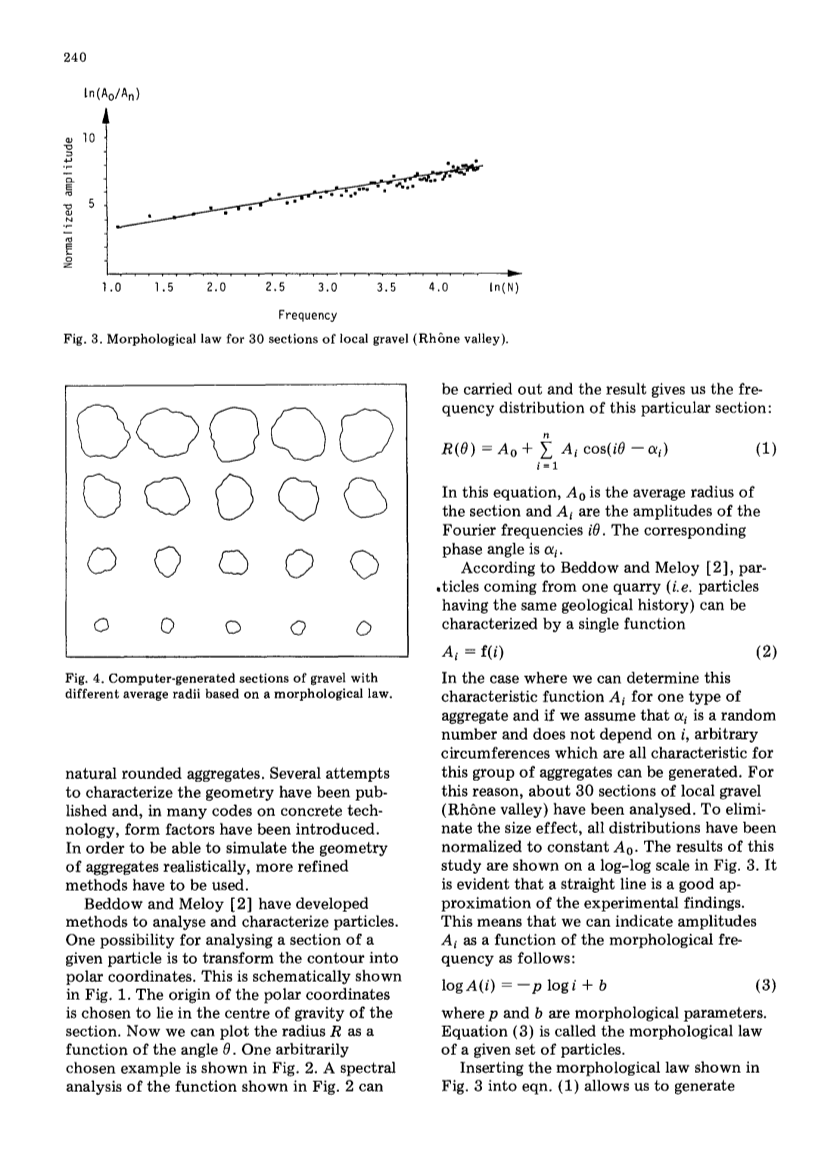
图3 30个当地碎石(罗恩山谷)截面的形状规律
图4 根据形状规律由计算机生成的不同平均半径的碎石截面
根据Beddow和Meloy的方法,来自同一的采石场颗粒(例如,颗粒有相同的地质历史)可以被同一个函数描述
(2)
在这个例子中我们可以确定同一类型骨料的特征函数Ai,如果我们假设alpha;i是一个与i无关的随机数,则可以生成任意周长,周长是这组骨料的特征量。由于这个原因,大约30个当地碎石(罗恩山谷)的截面可以被分析。为了消除尺寸效应,所有的分布被规范化为常量A0。结果以对数形式表示,如图3。这个结果证明实验结果很好地近似为一条直线。这意味着我们可以将振幅Ai写成一个形状频率函数,如下:
(3)
其中,p和b是形状参数。方程(3)被称为颗粒某一给定截面的形状规律。
将如图三所示的形状规律代入方程(1),我们能够生成这种类型颗粒的任意形状的截面。五组颗粒类型随机生成的截面如图4所示。
值得注意的是,这种方法适用于生成磨圆的截面,而碎石截面不能用这种方法进行模拟。参考文献3描述了模拟尖锐颗粒的方法。
(a) (b) (c)
图5 (a)给定骨料的粒径分布,由计算机生成二维结构(所有颗粒为球形);(b)模拟碎石混凝土,由计算机生成二维结构(所有的骨料截面替换为多边形);(c)模拟给定了骨料的粒径分布和形状特性(形状规律)的混凝土,由计算机生成二维结构。
图6 比较基于Walraven方法[4]从理论上预测二维累积粒径分布与被替代的计算机模拟:macr;macr;macr;macr;,数值的;···,理论的。只考虑直径为8-32mm的颗粒。
- 粒径分布
在截面2中,通过对平均半径进行规范化,我们有意消除了尺寸效应。为了能够生成真实的组合混凝土结构,我们必须考虑骨料的粒径分布,
一种给定了骨料粒径分布的组合结构如图5(a)所示。为了简便起见,在这个例子中,假设所有颗粒都为球体。截面中心随机选择。
另一个生成随机组合结构例子如图5(b)所示。在这个例子中,骨料被替换成多边形。边的数量和相应的角度都是随机确定的。这种类型的结构可以近似看做碎石混凝土。相似的结构被Zaitsev和Wittmann用于分析裂缝的发展。
图7 计算机生成的二维结构随试件结构距离方程的变化(边界效应)
图8 骨料、砂浆的相对体积浓度与试样表面的距离的函数(边界效应)
图9 组合结构的理想化有限元
- 用二维代替三维结构
原则上,利用与截面3相同的方法生成三维随机组合结构是可行的。然而生成组合结构的目的是研究这些组合材料的复杂特性例如变形能力、裂缝开展和扩散。解决这些问题的唯一可能就是使用数值分析。有限元分析是一个强有力的工具,但是当下计算机性能不足以支撑三维结构的研究,因此我们只能使用用二维代替三维结构。
有至少两种不同的方法将二维结构与相应的三维结构联系起来。根据统计学原则的基础,Walraven[4]能够在一个给定骨料粒径分布的无限组合材料中预测任意平面交叉点的粒径分布。Walraven研究了一种符合富勒颗粒粒径分布的特殊骨料。
三维组合结构被计算机模拟之后,可以采用一个完全不同的方法。任意平面的粒径分布可以通过近视的计算机分析得到。为了得到二维粒径分布统计图,需要大量分析任意选择的平面。
一个由这种方法得到的二维累积粒径分布如图六所示。与基于Walraven方法的理论预测进行比较如图。图六中的相互作用可以看做是一种二维粒径分布。在我们的例子中,它是一个二维富勒曲线。这个分布函数比三维分布函数发现小颗粒的可能性更高。这一结果可以解释为大颗粒对小颗粒的影响,如果它们被任意切割的话。
图10 比较组合材料各种有效弹性模量Ef骨料弹性模量Eg(弹性模量Em=2500Nmm-2;骨料体积浓度g=0.59);有效弹性模量在本工作中获得;曲线a,有效弹性模量取自
例如,根据相同的模型,曲线b,有效弹性模量取自
对于Poisson比=0.2,例如根据Hashin模型[5];曲线c,有效弹性模量取自,
例如根据连续模型。
一个组合材料随机截面分析可以应用在近表面区组成的研究。在混凝土技术中,混凝土表面区与内部材料有明显不同,称为边界效应。它证明了颗粒离表面的距离不会大于颗粒半径。因此,在近表面区中有大量的小颗粒。如果截面平行于表面,深度不断增加时,寻找大颗粒骨料的概率会稳步增加直到达到体积值为止。图7展示了一个例子。
当大骨料的数量增加时,硬化水泥浆体的含量增加,如图8所示。值得注意的是,这种情况下近表面区所有的材料性能(例如强度、变形、吸水性和混凝土干缩)都与内部不同。在普通混凝土和钢筋混凝土的耐久性研究中必须考虑这些不同。
图11 组合结构的有限元网格用于模拟水汽传输
-
一些应用
- 有效弹性模量
组合结构可以通过生成随机骨料完成建模。对于更进一步的详细分析,可以用有限元代替结构。图9显示了这个类型的一个例子。
这个结构可以真实地模拟水分扩散和热量扩散。为此,我们应该着重对组合材料有效弹性模量的确定进行讨论。假设这个矩阵的模量是一个常数,我们确定了组合材料的有效模量随骨料模数变化的函数。得到的结果如图10。10也给出了两种限制(如水平模型)。
图12 组合结构在水汽梯度常数下得水汽计算模型(从相对湿度100%到0%):(a)导致,(b)导致(c)导致,(d)导致。其中,是骨料体积,
是砂浆体积。体积率改变会被所有颗粒的常数因子模拟。
-
- 有效扩散系数
混凝土的扩散系数取决于它的含水率,这一事实在对干燥过程的实际估计中必须考虑进去,水分含量对扩散系数的影响可以在硬化水泥浆体的薄圆盘上测量。如果使用混凝土标本替代硬化水泥浆体的薄圆盘,混凝土标本会太厚从而导致不能够在合理的时间限制内进行测量,出于这个原因,能够预测出体积浓度对有效扩散系数的影响是必要的。为了解决这个问题,已经产生了具有圆形包裹体的混凝土的随机结构,聚集体的尺寸分布遵循二维富勒曲线。 已经考虑了直径在8到32毫米之间的骨料。 正如图9所述,这种复合结构必须用有限元网格来表示,以便进一步分析。 一个例子如图11所示。在这个结构中使用的扩散元素已经被专门开发,并且其细节将在其他地方描述出来[6]。 如果基体的扩散系数从实验中已知,则可以数值计算聚集体浓度的影响。 通过将所有颗粒的半径乘以常数来获得不同的体积浓度。图12所示的通过复合结构的流量已经在恒定水分梯度的假设下进行了计算。 图13表示了通过这种方式获得的扩散系数的降低,为了比较,还显示了并行模型的细小的结果。 数值结果表明,简单的几何方法低估了在实际意义范围内聚集浓度的影响
图13 计算得到的有效扩散系数是骨料体积率的函数:本文得到的结果;相同模型得到的结果。
图14 组合结构有限元网格用于分析过程和性能例如收缩,蠕变,断裂和非线性应力应变行为。结构由8000个有限元单元表示有特定性能的骨料,内部是水泥砂浆。
- 讨论结果和进一步的步骤
研究已经表明,通过使用形态学定律可以模拟天然骨料的随机几何形状。此外,还可以生成逼真的复合结构。必须特别注意将骨料的三维尺寸分布转化为二维尺寸分布。这种转换可以从适当的计算机分析中获得任意的分配函数。通过计算机模拟可以解释和确定近表面区域与大块材料的不同特性。复合材料的有效性能,如弹性模量和扩散系数可以进行数值的预测。图11所示的复合结构可以进一步扩展。例如,所有包含物都可以用有限元素表示。此外,可以使用适当的有限元素考虑接口的特定属性。由此产生的复杂有限元理想化的例子如图14所示。通过这种生成的结构,可以真实地模拟多孔复合材料的收缩和蠕变。同样的结构可以作为研究高荷载下裂缝形成的基础。这实际上是对Buyukoz turk等人早期工作的进一步发展。[7]和最近由Saito等人[8]和Venecanin [9],先进数值方法对于进一步推进具体科学的贡献将主要取决于与合适的实验工作紧密结合并逐步检查。
碱激发高岭土水泥对砂浆抗压强度的作用
Kornnika Wianglor,Sakprayut Sinthupinyo,Monow Piyaworapaiboon,Arnon Chaipanich
摘要
文章报告了两种养护方法下碱激发高岭土(MK)水泥的抗压强度和微观结构特性。MK被用于替代部分波特兰水泥(PC),替代的胶凝剂质量比为70,80,90, 95,100%。氢氧化钠(NaOH)和硅酸钠(Na2SiO3)被用作激发剂。使用的NaOH为10摩尔,碱溶液比胶凝剂为0.8,用水作为溶剂。水泥砂浆和新拌混凝土分别在23℃plusmn;2℃(55%RH)和60℃(95%RH)的条件下养护。结果表明,热重分析(TGA)检测到了水化硅酸钙(C-S-H)和碳酸钙(CaCO3)相。初凝时间和干缩随着偏高岭土替代水平的增加而下降,碱激发偏高岭土水泥的抗压强度随着PC水泥和温度的增加而增加。在60℃(95%RH)条件下养护试件能够增强抗压强度,基质比在23℃plusmn;2℃(55%RH)条件下养护会更为致密,(C,N)-A-S-H凝胶相和C-S-H凝胶相清晰可见。
1.介绍
波特兰水泥的生产过程是一个高能耗的过程,每生产一吨水泥会排放900kgCO2到大气中,这会导致全球变暖和气候改变。因此我们可以从水泥生产入手,通过用辅助胶凝材料(SCMs)替代部分波特兰水泥的方法减少二氧化碳排放。通常的SCMs包括偏高岭土和其他火山灰材料,它们在特定的条件下定制和煅烧,随后从高岭土中选择出来。MK有高活性,能够增加混凝土机械性能和耐久性。
“地聚合物”是一种替代
全文共9845字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12703],资料为PDF文档或Word文档,PDF文档可免费转换为Word


