
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
钢筋的可靠性分析混凝土框架
作者:R. Ranganathan and A. G. Deshpande
摘要:钢筋混凝土框架在破坏机制尚未形成之前,可能不会发生全弯矩重分布,任何临界区域可能因转动能力不足而失效。考虑到混凝土截面的有限转动能力,提出了一种方法来验证和分析已确定的主导机制是不可能形成的。提出了机构倒塌前旋转失效的可靠性模型,并利用失效阶段的弯矩重分配,建立了与机构相关并与机构一致的安全裕度方程。将旋转破坏模式与其他可能的机制模式相结合,重新评估结构的可靠性。给出了两个算例。研究发现,塑性铰转动的校核和破坏模式的重塑可以提高钢筋混凝土框架系统可靠性预测的准确性。然而,在简单框架的情况下,这种改进只是边际的。
简述:
框架结构的安全评估是一项非常困难的任务,因为由于荷载和阻力变量的随机性,结构可能会因为几个主要的倒塌机制中的任何一个而失败。研究人员正在开发框架结构可靠性分析方法,包括随机主导机构的自动生成(1,9-13,15,18,19)。这项工作的大部分主要是关于非常有延展性的结构系统(钢结构)。钢筋混凝土框架结构的可靠性分析是Ticky和Vorlicek提出的。他们制定了钢筋混凝土结构的可靠性,从一个或几个来源的荷载基于极限荷载,并显示了如何变形能力(延性)的关键区域可以考虑到研究钢筋混凝土框架。Webster提出了一个概率程序来预测钢筋混凝土框架在任意数量的连续试验荷载作用下的性能。Chou, Mcintosh和Corotis已经研究了具有已知倒塌机制的简单钢筋混凝土框架的抗力和可靠性之间的相关性。在文献中,它发现,钢筋混凝土框架的可靠性分析已经是最少参与的主题;在这方面所做的工作有限。
框架结构通过形成破坏机构而破坏,要求塑性铰具有较大的转动能力。在钢筋混凝土框架的情况下,任何临界区域,铰早,可能由于塑性旋转能力不足,在破坏机制形成之前,失效。这种失效模式称为旋转失效模式。考虑钢筋混凝土框架有限的塑性转动能力,提出了一种计算方法来验证和分析所识别的主导机制,并在必要时产生旋转失效模式。在部分利用铰链初始截面在破坏阶段的塑性弯矩能力的基础上,提出了一种与破坏机构相适应的可靠性模型。然后将旋转失效模式与其他可能的机制模式结合起来评估钢筋混凝土框架的系统可靠性。通过算例说明了该方法的有效性。
受弯钢筋混凝土截面的强度和刚度
理想模型
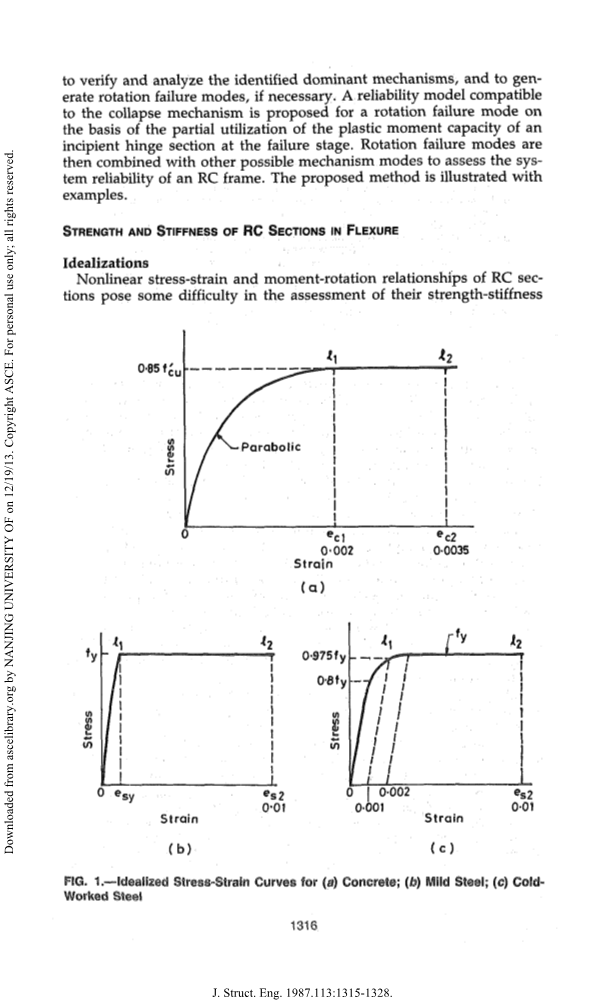
钢筋混凝土截面的非线性应力-应变和弯矩-旋转关系给钢筋混凝土截面的强度-刚度评估带来了一定的困难性,需要对钢筋混凝土框架进行可靠性分析。使用理想的混凝土和钢的应力-应变曲线(图1)和钢筋混凝土塑性铰的双线性弯矩旋转图[图。2(a)],建立了确定RG塑性铰弯矩承载力、抗弯刚度和转动承载力的计算方法。此外,为了简化结构分析,将非线性行为近似为线弹性和分段线弹塑性。同时,采用一阶二阶矩(FOSM)方法进行了可靠性分析。
图1所示。- (a)混凝土的理想应力-应变曲线;(b)低碳钢;(c) 冷轧钢
图2所示. - (a)钢筋混凝土塑性铰弯矩扭转图;(fo)铰链部分的塑性弯矩图
图2所示的极限l1和l2分别被认为是理想的弹性和塑性极限(2)。弹性极限l1对应的是混凝土中的最大压缩应变ecl等于0.002[图1(a)],或通过获得软钢棒的屈服应变esy而得到的钢的屈服[图1(b)],或高屈服强度变形杆的偏移应变为0.001[图1(c)],取决于首先达到的条件。图2(a)中/j对应截面的抗弯力矩称为屈服力矩My。混凝土或钢筋失效时达到塑性极限l2,对应于混凝土的最大应变ec2(取0.0035)[1(a)]或0.01的应变在钢[图。1 (b)或1 (c)]。截面l2处的抵抗弯矩取塑性弯矩M。
抗弯矩和抗弯刚度
矩形或三通截面在极限l1或l2的抵抗力矩可以通过满足力平衡和应变协调来计算。
如[图2(a)]所示:双线性力矩旋转图假定钢筋混凝土构件的抗弯刚度EI在0 ~ l1范围内为常数。同时,假设EI在构件的临界截面之间是常数。由应力和应变条件在极限处得到的均匀l1值由(2)给出
式中,c1 =中轴在极限l1处的深度,d =有效深度。
塑性抗剪力
图2(a)所示的钢筋混凝土塑性铰的转动能力theta;,是在恒定塑性弯矩下,由于塑性极限l2处的极限应变条件,截面能够维持的无局部破坏的角转动。截面的塑性旋转能力取决于(1)材料的性能;(2)加固量;(3)监禁比例;(4)轴向载荷。可将(2)扩展为(1)混凝土极限应变的函数;(2)混凝土从l1到l2的应变变化;(3)塑性区扩展,即塑性铰长度;(4)中轴位置。大量的实验研究表明,钢筋混凝土区域的塑性旋转能力有很大的变化。经验公式已被各种研究工作者报道过。Baker和Amarakone提出了一组曲线,表示在构件中不同比例的约束下,作为中立轴在极限l2处深度的函数,可代表允许的塑性旋转能力theta;P。这组曲线用于目前的工作。
塑性弯矩承载力统计
截面几何参数的变化通常很小,忽略不计。因此,为了建立M弯矩的统计量,只考虑frsquo;c(或frsquo;cu)和fy的随机变化。使用开发的M预测方程,并使用一阶近似,M的均值和标准差从fc(或fcu)和fy的已知统计量计算出来。
钢筋混凝土框架的可靠性分析
主导机构的自动生成
建立后钢筋的强度和刚度特性和统计的各种临界区,随机生成主导机制使用线性弹性和PWLEP的刚度法的分析结构和FOSM可靠性分析方法,假设一个最初无限旋转能力用于所有塑料铰链形成破坏机构。为了简化分析,假设轴向刚度(EA)和抗弯刚度(EI)是确定的。顺序选择最可能的铰链位置,确定将结构转变为失效概率较大的机构的塑料铰链组,是生成主导机构过程中的关键考虑。Murotsu或Ma 和 Ang或Tang 和 Melchers提出的方法可以用来生成随机优势机制;然而,作者开发的启发式搜索技术已被用于本研究中。
在ptwlep分析过程中,当结构刚度矩阵为奇异时,形成机构,最终铰链的安全裕度方程成为机构的安全裕度,根据假定的结构线性行为,第i节或在第i节有最后一个铰链的机构的安全裕度Zi表示为
式中, =临界截面塑性弯矩承载力; = 施加荷载; =单位弯矩M在第i段产生的弯矩;; =单位荷载引起的截面弯矩;m =临界截面数;n =负载个数。rsquo;,对于i = j, an = 1。
塑性铰不做功则=0,i=j的时候=1.
将随机变量M和Q分组在X中,安全裕度Zi及其均值micro;Zi和方差可以用矩阵形式表示为
Zi=[E]{X}
micro;Zi=[E]{micro;x}
=[E][Cx]
其中[E] =所有变量X的确定性系数和的行矩阵; =矩阵的转置[E];{micro;x}是所有随机变量X的均值的列矩阵;和[Cx] =所有随机变量的协方差矩阵Xj。可靠度指标beta;与安全裕度Zi的关系如下:
由于Zi是几个随机变量的线性函数,它趋向于具有正态分布(基于中心极限定理),而与单个变量的概率分布无关。因此,假设Zi为正态分布,则框架在破坏机构i下的失效概率为
式中()为标准化正态分布的累积分布函数。
结合并综合了以安全裕度Zi为特征的随机识别主导机制,通过计算边界来估计系统的失效概率。边界用Ditlevsen的方法计算
检查塑性扭转
生成随机主导机构的技术在的基础上选择塑料铰链,并确定将结构转换为机构的铰链组,而无需验证铰链区域的塑性旋转。这套铰链可以由不活动的铰链组成;此外,铰的顺序可能随荷载因子的变化而随机。当塑料铰链的实际塑性转动是要核对允许的塑性转动时,其物理过程中塑料铰链因载荷递增而连续发生的情况仅供个人使用;保留所有权利。必须考虑。因此,采用基于载荷系数的主导机构序贯分析方法,在序贯分析的各个阶段对铰链塑性转动进行检查,并计算出转动检查失败的失效概率。
假设塑性旋转集中在临界截面。因此,考虑截面塑性铰节点处的相对斜率为截面的塑性旋转,即图2(b)所示的不连续角。从分析中得到的节点的旋转,与节点上连接的构件完好端部的斜率相对应,而与铰接端部的斜率不相对应。构件铰接端处的斜度由相应构件的斜度挠度方程得到。那么塑性铰的转动,如图2(b)所示,是铰端斜率与相应节点转动的差值。
对已知活动铰链截面的机构按顺序进行再生,根据载荷系数检查铰链截面的转动情况。任意阶段潜在铰截面i的荷载系数ai为
在任何阶段,设选定的潜在铰截面为荷载系数ai最低的i,早期铰截面为j和k,在j(或k)处的实际塑性旋转theta;j为
图3所示。-在机构再生过程中检查铰接部分的塑性旋转
式中,Ms =临界截面塑性弯矩承载力s;Qt = 施加在结构上的荷载;和theta;jt=铰段塑性转动度数;rsquo;分别由单位塑性弯矩Ms和单位荷载Qt可知。非铰接截面的Ms对应的为零。theta;j-和theta;k可能分别超过允许的塑料旋转能力theta;pj和theta;。在这种情况下,不可能在图3所示的第i节形成铰链。如果theta;jgt; theta;pj;,则考虑旋转能力,载荷系数和,theta;j的关系如下
同理,如果是 gt; ,也可以得到负载因子的表达式,其中 = 。现在比较和,选择最小的,用表示。在这个值为R时,假定钢筋混凝土框架在机构形成之前,在旋转破坏模式下失效。由于旋转检查失败,第i部分的全部强度没有被利用。第i段塑性铰在荷载系数时形成;将系数aii改为
图4所示。-研究中的钢筋混凝土框架:(a)一隔间一层框架,例1;
(b)两隔间两层框架,例2
用方程中的值代替,2,建立了旋转失效模式的安全裕度 z,并利用方程组求出了旋转失效模式的安全裕度 z。3-7,计算可靠性指标,失效概率 。机制的再生过程在此阶段终止。
同样,所有先前确定的主要机制假设充分重新分配再生和分析; 此外,塑料旋转检查是执行铰接部分在每个阶段。将所有失效模式组合起来,确定系统失效概率的界限。因此,本文提出的钢筋混凝土框架结构可靠度分析公式包括以下几个步骤: (1)分析梁、柱的钢筋混凝土截面,建立 m 的统计量;(2)在假定截面无限旋转能力的情况下产生主导机制,并进行可靠性分析;(3)再生失效模式和检查铰接截面的塑性旋转;(4)综合所有失效模式并评估。 在Dec20系统上,在Fortran IV开发了一个计算机程序,用于提出RC帧可靠性分析的方法。 所提出的方法在下面的例子中进行了描述。
例1
- 一个简单的单湾一层RC框架如图所示。 4(a)。 负荷和材料强度变量的统计(14,16,17)给出了
表1.-RCFrame横截面的性能和变量的统计
例1
表2- 钢筋混凝土框架结构可靠度分析结果D ,
例1
见表1。 根据Turkstra的模型(21),考虑了以下两种负载组合的恒载,D,活载,L,风载,D 和D 。分别为和寿命最大活载和风载。 和分别为任意点时活荷载和风荷载。
利用给定的数据,建立了临界截面的性质和负荷和阻力变量的统计(表1)。 假设在所有关键部分的无限旋转能力,以形成机制,随机主导机制产生的负荷组合D 。已识别的机制及其安全裕度见表2。 计算了这些机制之间的相关性。 利用这些,建立了pare上的边界。 假设截面的无限旋转容量,框架的可靠性分析结果见表2。 每个确定的lsquo;机制是再生的塑料旋转检查铰链部分在每个阶段。 再生失效模式(机构模式和/或旋转失效模式)见表2。 计算了这些失效模式之间的相关性,并建上的界限,如表2所示。 该程序被重复,以评估系统可靠性下的第二负荷组合D 。 结果见表3。
案例b-对于同一帧,利用Lmax的统计量对负载组合D 进行了可靠性分析
表3. ー图4下钢筋混凝土框架结构可靠度分析结果 D
表4. ー钢筋混凝土框架截面特性及变量统计,例2
表5ーー钢筋混凝土框架结构可靠度分析结果 D
平均/名义=1.38和V=0.25[埃林伍德等人采用)。(7)]。 所有其他数据都是相同的。 结果汇总见表2。
例2例A-一个两湾两层RC框架如图所示。 4(b)。 载荷和材料强度变量的统计数据与表1中给出的相同。 表4给出了电阻随机变量截面的计算性质和统计量。 表5和表3分别给出了负载组合D 和D 下框架的可靠性分析结果。
案例b-对负载组合D Lm进行了同一框架的可靠性分析 利用LMM(7)的统计数据:平均/标称=1.38和V=0.25。 分析结果汇总见表5。
分析和结论
针对钢筋混凝土截面的极限转动能力,提出了一种简单实用的钢筋混凝土框架结构可靠度分析方法。通过对塑性铰转动的检验,发现该机构产生转动失效模式的概率高于无限转动能力机构,这是预期的。在表2、表4和表5所示的最不占优势机制的情况下,的这种增加是相当大的,对有限延性和完全再分布的结果的比较表明,对于有限延性,上的界限通常更高、更宽。
对有限延性和充分再分配结果的比较表明,对于有限延性而言,主应力集中系数的界限一般较高,也较宽。对于这两个案例,注意到在荷载组合 D 下框架的破坏概率大于在 D 下的破坏概率。在 D 条件下,有限转动容量对 的影响比 D 条件下更为关键。
根据参考文献[1]的设计方法,对钢筋混凝土框架的两个案例进行了研究。8)单层框架的系统失效概率为,两层框架的系统失效概率为,即表1给出的 统计值。这些失效概率的值非常小。这是由于高设计负荷和低材料设计强度指定的规范(8)。如果 的平均值与标称值之比为1.38,且 的变异系数为0.25(7) ,则系统失效概率
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[262594],资料为PDF文档或Word文档,PDF文档可免费转换为Word


