
英语原文共 9 页
组合应力或应变下的疲劳标准
George Sines George Ohgi
工程学教授 结构设计主管
工程学院, 波音商用飞机有限公司
加州大学, 西雅图,华盛顿州,98124
洛杉矶,加利福尼亚州,90024
摘要:本文简要介绍了先前提出的高周疲劳标准在交替和组合静态下的应力;针对高静态应力下的高周期疲劳提出了一个新的标准;概括了基于组合应力下的低周疲劳标准以及这些标准在主应力状态中所采用的形式;对主应力幅度之间的可变相位下的疲劳可能标准进行了推测;
第一章
简介:
由于疲劳破坏现象是一存在于局部部位的性质,我们研究时有必要仔细追踪施加在结构内的应力的路径。而结构的疲劳裂纹,可能会开始于一个有高交变应力作用的结构局部小区域内,此时即使结构的其余部分强度很高,疲劳裂纹仍然能够导致结构的完全失效。所以我们必须通过对结构构件的应力跟踪分析,分析结构构件内的应力分布,以找到高应力的关键区域。应力集中区的典型区域有铆钉孔、油孔、冲孔痕、螺纹根部和其他尖锐的凹角。
但问题是,在找到关键区域并计算其应力之后,人们如何知道应力的变化是可靠的? 这种应力通常不是简单的静态应力,而是交替法向应力和交替剪切应力的某种组合叠加在静态应力上。测试每种材料在组合交变应力和组合静应力的所有组合显然是不现实的,但我们必须从每种材料的常见实验室测试中做出一些估计。在本文第I部分和第II部分中,分析处理了结构在交替和组合静态应力下的疲劳性质,这是疲劳寿命的特征,通常称为“高周期”。“高周期”通常用于指定大于次周期的寿命。这种疲劳特征也可能与循环塑性应变为零或至少远小于循环弹性应变的应力水平下的失效有关。虽然有时塑性应变的初始阶段较短。但可能的是,循环弹性应变与循环塑性应变的比率是高周期的更一般性的描述,而不是循环周期本身。
在本文第三节中,对低周疲劳进行了一些概括和推测。“低周期”通常被认为是在维持时间小于次周期内发生故障的行为。然而,对低周疲劳研究的回顾表明,大多数数据是针对不到次周期的构件。低循环时的行为特征可能更好地与应力水平下的失效相关,在该应力水平下,循环塑性应变远大于循环弹性应变。一些材料,例如一些不锈钢[1]显示出持续的循环塑性应变,尽管在大于次周期的寿命时发生故障。它们的行为特征却可能类似于低周期而不是高周期的特性。
次周期到次周期之间失效特征的行为需要特别考虑。这种行为转变区域或可称为“中周期”。在这个区域,可能更重要的是确定在循环塑性应变和循环弹性应变具有相同数量级的应力水平下发生故障的行为。这个过渡地区的行为值得进一步研究; 在该区域下方,循环塑性应变与周期相关,而在其上方,循环应力确实存在。
第二章
1.高周期疲劳
现在已经提出了应力如何在高周期(周期大于)下引起疲劳失效的几个标准,但是它们都没有允许工程师充分利用材料的强度。 因为通常我们希望的是最小化运动部件的惯性力,以待提升部件的质量、尺寸以及成本,希望在不使用过多材料的情况下获得必要的强度。 在这里,我们将仅简要回顾典型的实验结果,这些结果导致标准的推广。 在参考文献[2,3和4]中提出或讨论了导致对高周期疲劳进行更多保守估计的其他概括。
2.压力描述
如果主应力以规则的正弦方式随时间波动,则可以通过叠加在静态应力上的交替应力幅度来描述它们。 在下面的介绍中,主应力将精确地处于异相或异相,并且所有主应力将以相同的频率变化。 尽管该标准将针对三轴应力制定,但感兴趣的应用通常是针对双轴应力的。 我们经常会关注应力为双轴的零件自由表面的应力,因为裂纹最常出现在那里。裂缝通常从表面开始,因为:
- 许多零件都有弯曲或扭曲力矩,因此会在表面产生最大的应力。
- 由于存在应力集中,例如划痕,工具痕迹和凹口,表面应力会进一步增加。
- 有充分的理由相信表面的颗粒在疲劳方面本质上较弱,因为一方面它们的变形不受相邻颗粒的限制。这已通过实验证实:如果疲劳试验中断并且试样的表面层被去除,则寿命可以大大延长[5]; 如果对试样表面进行有益的表面处理,例如喷丸处理,即使在轴向载荷下进行试验,其内部受到与表面一样多的应力,也可以大大延长寿命[6]。
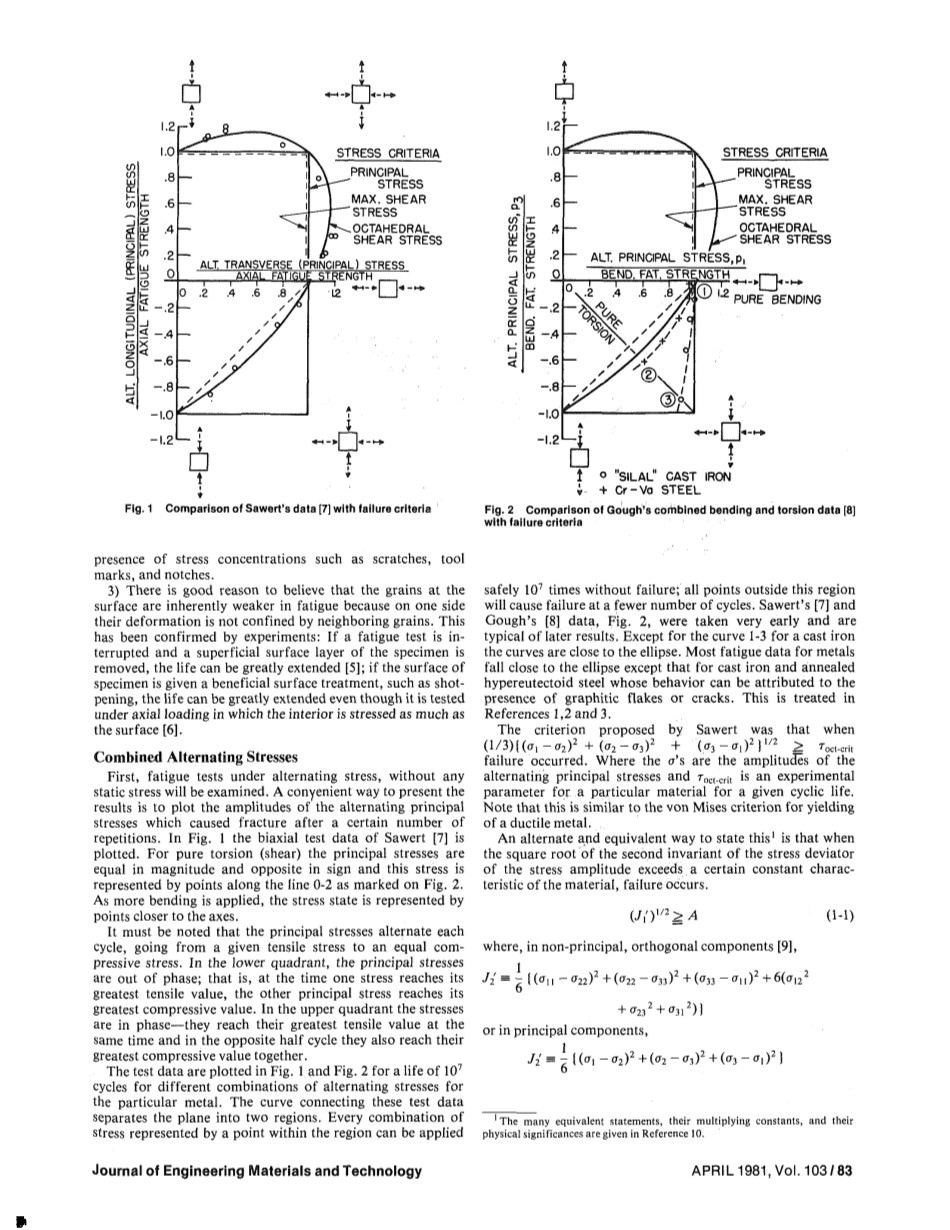
图1 Sawert数据[7]与失败准则的比较 图2 Gough组合弯曲和扭转数据[8]与失效准则的比较
3.组合交替应力
首先,将检查交替应力下的疲劳试验,没有任何静态应力。呈现结果的一种方法是绘制交替的主应力的振幅,这些主应力在一定次数的重复之后引起了试件断裂。 在图1中,绘制了Sawert [7]的双轴测试数据。 对于纯扭转(剪切),主应力大小相等且符号相反,并且该应力由沿着线0-2的点表示,如图2所示。随着施加更多弯曲,应力状态由点表示靠近轴。
必须注意的是,主应力在每个循环中交替,从给定的拉应力到相等的压应力。在下象限,主要应力是不同步的; 也就是说,在一个应力达到其最大拉伸值时,另一个主应力达到其最大压缩值。在上象限中,应力是同相的、同时达到它们的最大拉伸值,并且在相反的半周期中它们也一起达到它们的最大压缩值。
对于特定金属的交替应力的不同组合,测试数据绘制在图1和图2中,寿命为个循环。连接这些测试数据的曲线将平面分成两个区域。 由该区域内的一个点表示的每个压力组合可以适当地应用次而不会破坏;这个区域之外的所有点都会在较少周期内导致试件破坏.Swewert [7]和Gough的[8]数据(即图2)很早就得到了,且是后来结果的典型。 除了铸铁的曲线1-3之外,曲线接近椭圆。 而除了铸铁和退火过共析钢之外,大多数金属疲劳的数据曲线都接近椭圆,其行为可归因于石墨片或裂缝的存在。参考文献1,2和3对此进行了处理。
Sawert提出的标准是当这个公式出现问题时,其中是交替主应力的振幅,是给定循环寿命的特定材料的实验参数。注意,这类似于屈服金属屈服的von Mises标准。另一种说明这种情况的方法是,当应力幅度的应力偏差的第二个不变量的平方根超过材料的某个常数特征时,就会发生故障。
在非主要的正交分量[9]中,
或主要组成部分,
图3 平均轴向应力对轴向疲劳的影响[2,3,15]
图4 静态剪切应力对剪切疲劳的影响[21]
图5 静态剪切应力对弯曲疲劳的影响[2,3,15]
图6静态轴向应力对扭转疲劳的影响[2,3,9,15]
图7 静态和交变应力的不同组合对疲劳寿命的影响总结[2,3,15]
交替和静态应力的简单组合:
接下来,将发现静态应力对交变应力的允许幅度的影响并将其插入疲劳准则中。将检查下列简单组合的实验:
交替轴向应力的静态张力,见图3
交替轴向应力的静态压缩,见图3
交替扭转时的静态扭转,见图4
交替弯曲时的静态扭转,见图5
交替扭转时的静态张力,图6
交替扭转时静态弯曲,见图6
交替扭转时的静态压缩,图6
图3中关于静态压缩对交替轴向应力影响的数据是严格选择的;如果包括所有调查,总趋势将是水平的或相反的斜率[10]。在施加压缩时难以避免不受控制的弯曲,并且弯曲的存在会产生错误的结果。选择此处提供的测试是因为所使用的测试方法确保了真正的轴向载荷。
作者知道除了参考文献[1,2和3]之外,没有测试静态压缩对光滑试样上交替扭转的影响。然而,作者使用Seeger [11]对缺口试样进行了试验,扭转应力集中系数为3.2,缺口根部的静态压应力等于钢材的屈服强度。这在图6中有示出。
而静态应力和变化应力测试的组合结果如图7所示。仅给出了曲线的线性部分。 当发生过度屈服时,曲线会从所示的线性关系中迅速下降。
检查图7的中心柱,标题为剪切应力最大交替平面上的静态应力,表明当总和为正时,与情况a和e一样,静态应力增加减少允许的应力交替。当总和为负时,与情况b和f一样,允许的交替增加。 并且当总和为零时,无论施加的静态应力如何,如在情况c和d中,静态应力都没有影响。因此,在应力交替和作用在最大剪切交替平面上的静态法向应力之和之间似乎存在简单的相关性。
由于正交法向应力的总和取决于它们的方向,因此实际上没有必要检查最大剪切交替的平面; 两个正交平面的相关性在任意两平面都可以看到。因此,可以说,对于给定的疲劳周期,静态应力的允许幅度是静态应力的第一个不变量的函数。对于三轴应力也是如此; 最大剪切面不是相互或正交的,但它们上的法向应力之和仍然是。
叠加静应力疲劳破坏准则:
根据已经呈现的疲劳数据,可以提出一个标准,其包括交替应力与静态应力的不同组合的效果。 对于不会过度超过数据的压力,简单的线性关系是合理的。如式(1-2)-
在参考文献[10]中,对Dehlinger和Novozhilov的工作进行了审查。他们都表明与所有平面上剪切应力的均方根成正比。在附录中,显示与所有平面上的法向应力的平均值成比例。因此,对等式(1-2)中给出的标准的物理解释是,对于给定的循环周期,在所有平面上剪切应力的均方根交替的允许幅度是在所有平面上平均的静态法向应力的线性函数。
虽然这公式是以暗示它对三轴应力有效的方式编写的,但在三轴应力下采集的数据太少,不足以证明这一点。对于双轴应力的情况,有相当多的实验证据和许多工程应用,我们可以在正交的非主成分上写出交变应力的幅度即:
或是正交的主成分即:
而静态应力的双轴形式是:
等式(1-2)的A和是循环周期的函数,对于该标准可能应该大于次.为了找到给定周期的A和,我们需要通过测试得到所需疲劳周期的实验确定两个不同的值,插入两个不同应力状态的标准,导致在相关的循环周期中失效,给出两个同时代数A和的方程很容易解决。
图8 双轴交变应力双轴静态应力的高周期疲劳准则
图9 作为R值函数的双轴交变应力的高周期疲劳标准
图10 高周期疲劳准则表现为三轴主应力空间中的表面
标准的图形表示
对于自由表面,该标准以图形方式呈现在图8中。在自由表面处,一个主应力为零,因此允许将其函数绘制为另外两个主应力的二维函数。它看起来像一系列“同心”椭圆,椭圆的大小取决于静态法向应力的总和。静态应力之和越大(拉应力),椭圆越小; 相反,总和越负,椭圆越大。静态应力之和越大(拉应力),椭圆越小; 相反,总和越负,椭圆越大。图9给出了作为R=最小应力/最大应力的函数的标准。
如果静态应力是固定的,则可以选择允许的交替应力振幅组合。 选择对应于静态应力之和的椭圆,并且该区域内的交替应力的任何组合都是安全的; 相反,外部的所有组合都会导致过早失败。如果要将标准应用于所有三个主应力均不为零的物体内部,则图形表示变为三维图,其中第三主应力与另外两个主应力正交。该空间中的破坏面是一个圆柱面,其发生器具有方向余弦(,,),与二维表示中的椭圆轴的平面相交[12(第57页)]。(见图10)
但推广到三维时,该标准的有效性从未得到证实。当应用于中间区域时,它可能是偏保守的,因为测试数据是采用在固有较弱表面上引发故障的试样收集的,但是当它应用于具有作用于其上的牵引力的表面区域时, 任何机械接触或高压流体的作用都可能使其预测不保守。
通常,该标准不能仅通过插入应力来用于预测疲劳寿命。一般的,临界局部区域处于某种应力集中。其中可能存在残余应力[13,14],其中压力加剧,压力状态可能会发生变化[15]。 此外,还必须考虑材料的疲劳缺口敏感性[16]。
II高静(均值)应力
通常认为结构构件在由于疲劳裂纹的发展而发生破裂时疲劳失效。疲劳裂纹在关键节点中开始并在整个构件中发展,伴随着额外的应力循环,直到破裂发生。在高周期疲劳中,对裂纹扩展的研究表明,可见裂纹在部件中的发展仅在部件的总疲劳寿命的很小百分比中发生。为了简化分析,将假设缺口部分的疲劳强度部分地与关键元件的强度同义。尽管在许多应用中静态应力很低,但是当循环的最大应力超过时,在标准(方程(1-2)中表示的线性关系是有效的。 屈服强度提高约30%至50%后,线性行为不再持续,见图5b。(注意图3中横坐标表示的是平均应力/屈服强度,而不是最大应力,即平均应力加上交替应力幅度;因此,大部分数据的最大应力高于收益率。)我们现在将修改标准,以解释峰值应力明显超过屈服强度的情况[17]。压力不变量的基本表达是:
其中最后一个术语用于解释宏观非弹性效应。 指数a是一个实验参数。在方程(1-1)和(1-3)中给出了一般三轴或
资料编号:[4917]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


