
英语原文共 16 页
荷载路径对纤维增强聚合物(FRP)约束钢筋
混凝土性能的影响
吴宇飞 曹玉贵
摘要:本文介绍了对纤维增强聚合物(FRP)约束钢筋混凝土柱在恒定轴向荷载和增大弯矩作用下的试验研究。共计55个砼柱体,以FRP厚度和轴压比为变量,对砼柱进行了试验研究。与另一种恒定弯矩和增加轴向荷载的荷载路径相比,这种加载方案下的砼柱荷载响应有很大的不同。结果表明,荷载路径对FRP约束混凝土的应力-应变特性有显著的影响,不同荷载路径下的FRP约束混凝土需要不同的应力-应变模型来阐述。根据试验结果,提出了FRP约束混凝土在相应荷载路径下的应力-应变模型。DOI:10.1061/(ASCE)CC.1943-5614.0000799.2017年美国土木工程师协会。
关键词:混凝土、柱、应力-应变关系模型、荷载路径、约束、纤维增强聚合物(FRP)
简介
纤维增强聚合物(FRP)因其在加固、加强和修补钢筋混凝土柱方面的高效率而成为一种流行的加固、改进和修补方法。在以轴向荷载作用下的FPR加固混凝土的研究已有大量文献报道(Fardis and Khalili 1982; Ilki et al. 2004; Kono et al. 1998; Lam and Teng 2003; Mirmiran and Shahawy 1997; Saafi et al. 1999; Samaan et al. 1998; Shehata et al. 2002; Wu and Wang 2009; Xiao and Wu 2000, 2003; Youssef et al. 2007; Wei and Wu 2012; Wu and Zhou 2010; Harajli 2006; Wu et al. 2006)。然而,对于FRP约束混凝土柱在轴向荷载、弯矩和偏心荷载作用下的受力情况,人们所知甚少(Song et al. 2012; El-Maaddawy and El-Dieb 2011; Hadi 2007; Hadi and Widiarsa 2012; Li and Hadi 2003; Parvin and Wang 2001; Wu and Jiang 2013a)。 基于现有知识 (El-Maaddawy and El-Dieb 2011; Song et al. 2012; Hadi 2007; Hadi and Widiarsa 2012; Li and Hadi 2003; Parvin and Wang 2001)和最新的发现 (Wu and Jiang 2013b)FRP约束混凝土柱在轴向荷载和弯矩组合作用下的受力性能与同轴轴向荷载下的性能有显著差异。轴向受压柱的应力-应变模型不适用于偏心受压柱(Wu and Jiang 2013b)。 换句话说,FRP约束混凝土柱的应力-应变特性与荷载路径有关。
对钢筋混凝土柱(不加其他约束)的荷载路径相关性进行了试验研究(Li et al. 1988; Bousias et al. 1992; Qiu et al. 2002; Bechtoula et al. 2005;Rodrigues et al. 2015)。Bousias等人(1992)研究了在恒定轴向荷载下八根双轴载荷路径的钢筋混凝土柱能量消散。Qiu等人(2002)研究了七种载荷路径下钢筋混凝土柱的承载能力。Rodrigues等人(2015)研究了在六个水平载荷路径下具有不同轴向载荷的钢筋混凝土柱。实验结果表明,荷载路径对钢筋混凝土柱的非线性行为,延性和承载能力有显着影响。
很少有关于FRP约束混凝土柱的荷载路径相关性的测试报告。Wu and Jiang提出了恒定偏心和增加轴向力作用下的FRP约束混凝土柱的应力-应变关系模型(2013b)。但是,不可知该模型是否适用于其他载荷路径下的偏心承载混凝土柱(例如在恒定轴向载荷下但增加偏心距)。而这项工作的目的就是研究FRP约束混凝土柱的应力-应变行为与载荷路径的相关性。
实验设计
在这项工作中共试验了55个混凝土柱。试验变量是FRP厚度、混凝土等级和轴向力。在恒定轴向力和逐渐增加的弯矩下试验所有试件。试验记录包括FRP约束混凝土的弯矩与曲率曲线和横向应变。从试验结果中获得了弯矩和轴向力之间的关系(M-N相互作用图)。在这种加载方案下,试验数据还可用于开发FRP约束混凝土的应力-应变模型。
标本设计
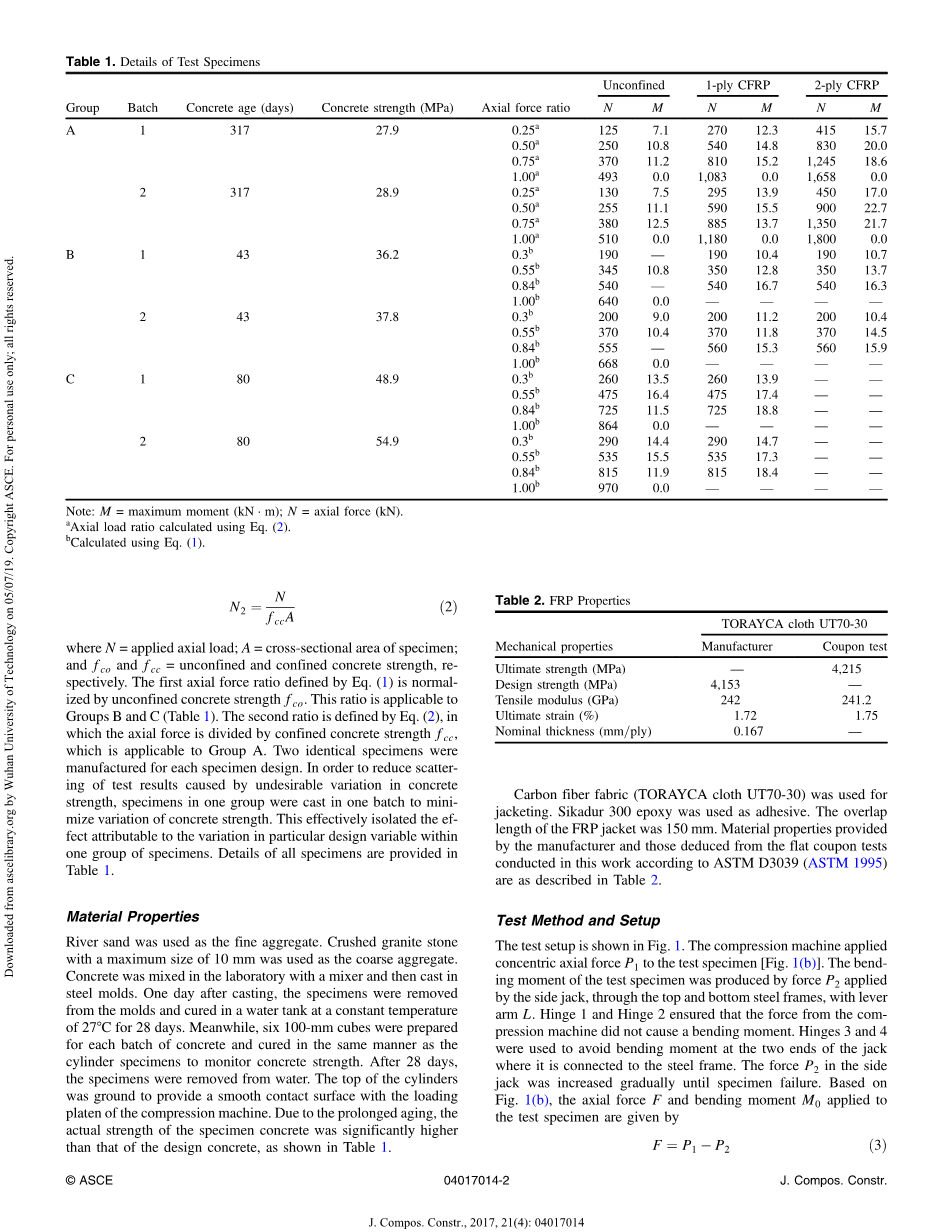
试件的直径为150mm,高度为300mm。CFRP有三种厚度:0层、1层和2层。A,B和C三组混凝土强度分别采用C20、C30和C40。测试中涉及八种不同的轴向力值(表1)。针对不同的试件组定义了两个轴压比
(1)
(2)
表1.试件的细节
注: M =最大弯矩(kN·m),N =轴向力(kN);
a轴压比使用公式1计算;
b使用公式2计算。
其中N为施加的轴向荷载,A为试件的横截面积,和分别为无约束和约束混凝土强度。公式(1)定义的轴压比中使用的是无约束混凝土强度,该比率适用于B组和C组(表1);公式(2)定义第二种轴压比,其中轴向力除以约束混凝土强度,适用于A组(表1)。每种设计试件设置两个相同的试件。为了减少由混凝土强度的不确定性变化引起的试验结果的误差,同一组中的试件以最小化混凝土强度的变化一次性浇筑,这有效地避免了同一组试件内由特定设计变量变化带来的影响。所有试件的详细信息见于表1。
材料特性
砂石作为细骨料。最大粒径为10mm的碎花岗岩石作为粗骨料。混凝土在实验室中用混合器混合,然后浇筑在钢模中,浇筑后一天,将试件从模具中取出并在27℃的恒温水箱中固化28天。同时,每批混凝土准备6个100mm与钢模中试件相同配合比的立方体,用于测试混凝土强度。28天后,将试件从水中取出。打磨砼体顶部以提供压缩机加载压板的平滑接触表面。由于养护时间延长,试件混凝土的实际强度明显高于设计混凝土,如表1所示。
碳纤维织物(TORAYCA UT70-30)用于加固,Sikadur 300环氧树脂作为粘合剂。FRP的重叠长度为150mm。制造商提供的材料特性以及根据ASTM D3039在本工作中进行测试推导出的材料特性(ASTM 1995) ,如表2中所述。
表2 FRP属性
测试方法和设置
测试设置如图1所示。压力机将轴心力 施加到试件上[图1(b)],通过侧面千斤顶施加的力,通过顶部和底部钢框架,杠杆臂L产生试件的弯矩;铰链1和铰链2确保来自压力机的力不会产生弯矩;铰链3和4用于避免在千斤顶两端连接至钢框架处产生弯矩;侧面千斤顶中的力逐渐增加,直到试件破坏。基于图1(b),施加在试件上的轴向力F和弯矩 由下式给出
(3)
图1 测试设置:(a)试验台;(b)测试计划
(4)
其中L为从 到的距离,如图所示1(b)。
在测试开始时,首先通过、=0施加预先设计的轴向力F,后逐渐增加力,为了在测试期间保持恒定的轴向力F,也要根据的读数手动增加,使得-恒定。以这种方式,在恒定轴向力和增大弯矩作用下测试试件直至破坏。
设备
通过压力机的内部测力传感器测量轴向荷载。用另一个称重传感器测量荷载(图1),数字图像相关系统(DIC)是一种可以在测试过程中连续捕获位移和应变的测量技术,用于捕获试件极端压缩面(最大压缩面)的表面变形[图2(a)]。已经有研究证明DIC系统对于各种类型实验中试件表面应变的连续测量是非常有效和准确的 (Yun and Wu 2011; Wu and Jiang 2013a; Jiang et al. 2014; Wu et al. 2015; Wu and Jiang 2013c)。其他七个应变仪(#2至#8)用于测量图2(a)所示位置的侧向应变。使用180mm标距长度的四个LVDT来测量试件的轴向变形和曲率,两个安装在最小压缩侧,另外两个安装在最大压缩侧[图2(b)]。LVDT到试件最外层纤维的距离为11.5mm [图2(b)]。通过LVDT和DIC同时测量试件最大压缩侧的垂直应变,并且通过LVDT监测最小压缩侧的垂直应变。在测试期间,通过自动数据采集系统记录所有测量值。
图2 仪器设备:(a)DIC系统;(b)以mm为单位的LVDT测量
测试步骤
标本测试使用以下程序中的步骤:
1、将试件固定在安装了四个LVDT的铝框架中[图2(b)];
2、将力增加到普通混凝土试件承载能力的约30%。在此过程中,顶部和底部用于施加弯矩的框架始终保持水平[图1(a)]并且=0;
3、调整试件的位置,使四个LVDT的读数相同(差异lt;10%)。在这种情况下,试件在下被认为是同轴心负载;
4、将压力机的压力改为其设计轴向力F(表1)。通过增加的位移(每次增加约2.5 mm)来施加小的增大曲率;
5、读取 的值并将压力荷载增加到,保持恒定的轴向力;
6、转到步骤5,使应用另一个增量位移并重复此过程,直到试件破坏。
实验结果和讨论
破坏模式
不同轴压比的所有试件的典型破坏模式示于图3(a–c)中对应A组和图3(d–f) 对应B组和C组,由于轴向力较小,B组和C组试件的破坏程度(混凝土破碎程度和FRP破裂)通常小于A组试件。对于轴压比最小的的试件,试件张力侧出现横向拉伸裂缝,随着弯矩的增加裂缝进一步加宽。FRP条带的断裂主要在最大压缩侧附近。对于具有较高轴压比和0.84的试件,FRP和混凝土破坏区的尺寸随轴向力的增加而增加[图3(e和f)]。
荷载-变形曲线
对于典型的标本,弯矩与LVDT位移曲线如图4所示。每个试样有两条曲线,一条来自最大压缩侧的两个LVDT的平均读数,另一条来自最小压缩侧的两个LVDT的平均读数。压缩位移是正的,拉伸位移是负的。LVDT的位置如图2(b)所示。
对于A组中轴压比相对较小的试件和0.5 [图4(a和b)],弯矩在达到峰值后略有下降。在峰值弯矩附近存在屈服平台,平台的高度随着轴力比的增加而减小。对于轴压比为的试件,屈服平台几乎不存在,弯矩在达到峰值后迅速下降。与A组中的样本相比,B组和C组中的样本[图4(c–e)]在最终破坏之前通常具有较大的变形,这显然是由这两组中较小的轴向力引起的。从曲线可以看出,轴向力对弯矩-位移曲线的影响比FRP的厚度更显著。表1中总结了所有试件的峰值弯矩和轴向力。
图3 破坏模式:(a)N2 = 0.25;(b)N2 = 0.5;(c)N2 = 0.75;(d)N1 = 0.3;(e)N1 = 0.55;(f)N1 = 0.84
图4 弯矩 - 位移曲线:(a)A组,1层,第1批;(b)A组,2层,第1批;(c)B组,1层,第1批;(d)B组,2层,第1批;(e)C组,1层,第1批
曲率和应变的计算
试件变形如图5所示变量, 和分别是顶部和底部框架试件的最小压缩侧和最大压缩侧的长度。测试前顶部和底部框架的原始距离为180 mm。 因此,LVDT的标距长度为。其他尺寸如图5所示。如果最小和最大压缩侧的LVDT分别为和的读数,则这两个LVDT位置的长度分别为 和。
基于图5中的几何关系可以获得以下关系
(5)
(6)
此外
(7)
变量和等于
(8)
(9)
试件的最小和最大压缩侧的应变和分别由下式给出
(10)
(11)
试件的曲率可以下式通过计算
(12)
式(12)用于计算试件的曲率,弯矩用公式(4)计算,所有试件计算出的弯矩与曲率曲线如图6所示。
图5 曲率的计算
对于处的第一点,仅对A组试件进行了约束混凝土强度的测试,因此,第一点的实验结果仅适用于A组试件。对于B组和C组的试件,这一点是根据Wei和Wu的约束混凝土理论模型计算出来的(2012)。
对于的最后一点,如果忽略拉伸阻
资料编号:[4469]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


