
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
高速铁路桥梁桩基长期沉降预测
杨奇,冷伍明,张升,聂如松,魏丽敏,赵春彦,刘维正
1.中南大学土木工程学院,长沙410075;
2.中南大学交通运输工程流动博士后流动站,长沙410075
copy;中南大学出版社和Springer-Verlag柏林海德堡2014
摘要:首先通过现场研究和分析,得出了高速铁路桥梁桩基加载的过程和特点,并给出了相应的加载功能。在多级加载下,采用单排水或双排水,建立了弹性多层土的一维固结方程。此外,计算有效应力和沉降的公式来自拉普拉斯数值反演变换。改进了桥梁群三维复合分析方法,模拟了桩基的实际荷载工况,并考虑了桩下土层的固结特性。最终,开发了一个名为LTPGS的相应程序来提高计算效率。对该方法得到的长期沉降与桩基现场测量的对比进行了说明,得出了一致性。计算结果与测量结果之间的误差小于1 mm,并且随着时间的推移逐渐减小。结果表明,该方法能够有效地模拟桩基的长期沉降,程序LTPGS可以提供可靠的估算。
关键词:桥梁桩基;长期解决;合并;拉普拉斯数值反演变换;多级装载;多层土壤
1介绍
为确保轨道的长期稳定性和一致性,严格限制高速铁路基础的工后沉降。由于桩基可以减少沉降,增加承载力,因此在全线铁路桥梁工程中得到广泛应用。因此,桩基工后沉降的控制是基础设计的关键技术之一,其中长期沉降的预测是一个关键问题[1]。
许多用于预测桩基沉降的方法可以在已发表的文献中找到,即经验方法[2],2)基于相互作用因子概念的方法和叠加原理[3-4],3)等效筏板或墩法[5-6],4)数值方法,如有限元法和有限差分法[7-8]和5)基于事先现场测量沉降的经验预测方法[9] 。
上述各种方法都是以桩基沉降为主,而桩基长期沉降等时间沉降则忽略不计。在某些情况下,它可能会导致某些结构中出现严重问题,例如高速铁路,特别是位于深层软土地层中,其严格控制沉降。因此,研究桩基长期沉降的分析方法是十分必要的。最近,对这个重要问题进行了一些调查。基于弹性理论,提出了估算桩基工后沉降的方法[10]。建立了一种计算长期沉降的简单实用方法,其中Mesri蠕变模型用于模拟桩尖下土的性状[11]。采用有限元法[12]研究了桩基的时效沉降和参数分析。采用粘弹性模型模拟土体的蠕变特性,采用拉普拉斯变换法对桩基进行长期沉降分析[13]。考虑到非均匀地基土的粘弹性变形特性,建立了桩基粘弹性沉降计算方法[14]。推导了非线性粘弹性土中轴向受压桩的闭合解,并开发了相应的GASPILE程序来研究桩的蠕变性能[15]。提出了一种单桩时效沉降分析方法,采用虚拟土桩模型和桩周土的粘弹性[16]。进行三维有限元固结分析,研究桩筏基础的时间沉降行为[17]。模型试验表明,桩的时变位移主要归因于桩/土界面的蠕变和桩周土的剪切蠕变[18]。提出了一种预测桩基长期沉降的新数学模型,其中土壤表现为粘弹塑性介质[19]。采用FEM-FDM方法进行了土-水耦合分析,评价了软土地基中桩基的长期位移[20]。采用有限元方法研究桩筏基础的安慰沉降特征[21]。众所周知,桩基荷载的特征是多层次的,其值随着梁,混凝土基础,轨道板和轨道等墩身和上部结构的施工过程而增加。在上述方法中,很少关注负荷的时间效应,这对预测长期结算具有重要影响。
在这项工作中,基于LENG等人[22]提出的桥梁群三维复合分析方法,提出了一种长期沉降分析的实用方法来模拟桩基的实际荷载状态和固结。桩下土层特性。开发了一个名为LTPGS的相应程序以提高计算效率。本文将对京沪高速铁路桩基的全面现场试验进行研究,验证该方法的有效性和准确性。
2高速铁路桥梁桩基承载特性
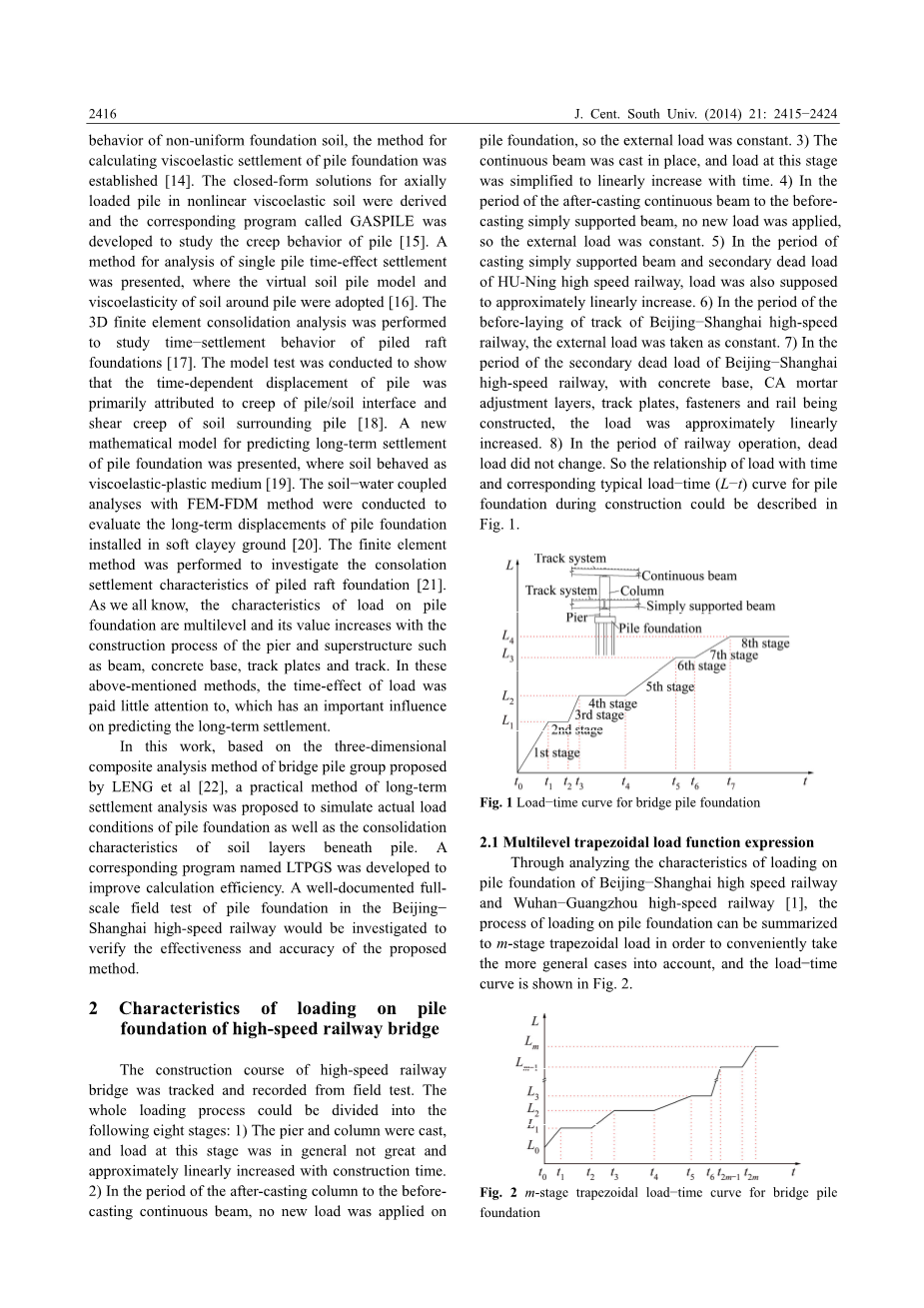
通过现场试验跟踪和记录高速铁路桥梁的施工过程。整个加载过程可分为以下八个阶段:1)铸造墩和柱,此阶段的载荷一般不大,随着施工时间近似线性增加.2)在后浇铸期间在预制连续梁的柱上,桩基上没有施加新的荷载,因此外部荷载是恒定的。3)连续梁浇铸到位,此阶段的载荷简化为随时间线性增加。4)在铸造后连续梁到铸造前简支梁的期间,没有施加新的载荷,因此外部载荷是恒定的。5)在HU-Ning高速铁路的简支梁和二次静载铸造期间,载荷也应近似线性增加。6)在京沪高速铁路铺设前轨道期间,外部载荷为常数。7)在京沪高速铁路二次静载期间,混凝土基础,CA砂浆调整层,轨道板,紧固件和轨道施工,荷载近似线性增加。8)在铁路运营期间,静载没有变化。因此,施工期间桩荷载与时间的关系以及相应的典型荷载-时间(L-t)曲线可以在图1中描述。
图1 桥梁桩基础的荷载-时间曲线
2.1多级梯形载荷函数表达式
通过分析京沪高速铁路和武广高速铁路[1]桩基荷载特性,将桩基荷载过程概括为m阶梯形荷载,以便于取得。更一般的情况考虑,负载时间曲线如图2所示。.
图2 桥梁桩基m阶梯形荷载-时间曲线
据报道,随着时间的推移,桩下土体荷载规律与桩基础荷载随时间的变化规律一致[23-24],因此桩下土体荷载随时间的变化曲线如图2所示。m阶梯形载荷-时间曲线的数学表达式可以如公式1所示。
图3 桩下土的m阶梯形荷载-时间曲线
.
.
(1)
其中m=1,2,hellip;,n
注意,加载函数L(t)的表达形式与加载函数q(t)的表达形式相同,因此L(t)可以仅通过符号L替换符号q来获得。
2.2q(t)的拉普拉斯变换
q(t)的拉普拉斯变换公式是.其中s是拉普拉斯变换参数.1)多级荷载应用于高速铁路桥梁桩基础,梁的施工属于现场沉降混凝土。用方程式代替(1)进入Eq(2),q(t)的拉普拉斯变换表达式推导为
当t1 t 0 : ,
= (3a)
当t2 t t1:,
(3b)
当t3 t t2:,
(3c)
当t4 t t3:
(3d)
当t5 t t4:,
(3e)
当t t5: ,
(3f)
可以分析等式并将其引入的统一表达式中,如等式1所示。 图。
当t2m-1 t t2m-2:,
- 当m=1,
(4a)
- 当mgt;1,
(4b)
当t2m t t2m-1:,
(4c)
2)高速铁路桥梁桩基施加三级荷载,梁施工属于现场安装。
当t1gt;tge;t0,t2gt;tge;t1时,表达式与Eqs相同。图(3a)-(3b)。
当t3 t t2:,
(5a)
当t4 t t3:,
(5b)
当t t4:
(5c)
3层状土的一维固结分析
饱和层状土的一维固结计算模型如图4所示。任意层索引为i(i = 1,2,...,n)。第i层的土壤性质是压缩系数Ei,垂直渗透系数kv,i,体积压缩系数mv,i和固结系数cv,i;土壤顶面到第i层土壤按钮的深度为hi;表面顶部的载荷为q(t);深度Z和时间t的垂直有效应力的增量为i(Z,s)。假设土壤层的顶部表面是可透过的,而底部的表面是透水的或不透水的。
图4分层土的一维固结计算模型
3.1一维固结方程
考虑到超孔隙水压力,饱和土中的一般一维固结方程可写为[25],
(6)
其中u是超过孔隙水压力,取决于Z和t,Z是空间坐标,t是时间; 是水的单位重量;是土壤的浮力单位重量,H是土壤的厚度。假设层土的厚度随时间变化等于零,,并且渗透率随时间的垂直系数是常数,。对于第i层土壤,多级荷载下一维固结的控制方程可写为
(7)
有效压力的原理如下:
(8)
代入等式(7):
(9)
然后执行方程的拉普拉斯变换。等式(9)它可以写成:
(10)
其中
初始条件如下:
(11)
考虑到土壤为连续介质,相邻土层之间的连续条件如下:
- 压力的连续性条件是:
(12)
(2)流动的连续性条件是:
(13)
边界条件I:土层顶面是透水的,而底层是不透水的:
(14a)
边界条件II:土层的顶部和底部表面都是透水的:
(14b)
用拉普拉斯变换进行等式(11),然后将其代入等式(10),然后求解方程式(10)可以表示:
(15)
其中参数,和是系数。
通过执行方程的拉普拉斯变换。等式(12)-(13),等式(16)-(17)可以得到如下:
(16)
(17)
矩阵Di和Mi定义为方程组(18)-(19)来自方程组(16)-(17):
(18)
其中 (19)
通过使用矩阵Di和Mi,矩阵也可以如下表达:
(20)
其中变换矩阵
全文共15200字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2726]


