
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
两高层建筑间风压分布的干扰效应
余先锋1 谢壮宁1 朱剑波1 顾明2
(1. 华南理工大学亚热带建筑科学国家重点实验室,510640,广州;2. 同济大学土木工程防灾国家重点实验室,200092,上海)
摘要:通过采用同步测压技术,研究了两个高层建筑在串列,斜列以及并列布置时风压干扰效应。布置方式包括六种不同的宽度比(Br=Binterfering/Bprincipal)和四种不同的高度比(Hr=Hinterfering/Hprincipal)。并进一步研究了最不利的并列布置模式下风压分布效应的特性。结果表明:由于遮挡效应平均风压大多是对结构有利的,然而邻近施扰建筑的侧面峰值风压主要呈现放大效应。随着宽度比和高度比的增大,相应的屏蔽和放大效应变得更加显著。当串列布置下的高度比小于1时,由于三维绕流现象,使得受扰建筑侧面局部平均风压和峰值风压分别升高了56%和53%。并列布置时的狭管效应引起足够的重视,根据观察,平均风压和峰值风压的最大峰值风压干扰因子分别达到了2.6和1.91。最后运用高精度的线性回归方程展现了并列布置下的最大块干扰因子和建筑间距之间的关系。
关键词:高层建筑;干扰效应;风压分布;狭管效应;回归方程
1引言
随着现代高层建筑高度和强度的不断增加,高层建筑之间的干扰效应变得越来越复杂。很多研究者已经研究了这个课题(Sykles, 1983; Bailey and Kwok,1985; Taniike, 1992; Xie and Gu, 2004, 2007; Lam et al, 2008, 2011; Mara et al, 2014)。然而这些研究者主要聚焦在总体风荷载以及静力或动力干扰效应。很少有人讨论现实中由于干扰效应而发生的高层建筑损坏,然而建筑附件,特别是幕墙经常会被强风吹坏。Sparks et al. (1994) 研究了沿海城市由于飓风导致建筑结构破坏造成的经济损失,发现超过一半的经济损失源于建筑附件破坏。
由于高层建筑风荷载干扰效应的复杂性,很少有系统性的研究对其进行测试。通过风洞试验,Gowda and Sitheeq (1993) 研究了建筑物间距对串列布置的顺风向结构的表面风压力的干扰效应,发现当建筑物间距较小时,顺风向建筑完全沉浸在逆风建筑的剪力边界层中。因此,整个结构迎风面承受较高的负压。
Joacute;iwiak et al. (1995) 对一个11层的结构进行风洞试验,发现在建筑物间的间隙区域,背风面的局部负压比单体建筑物测得的数值要高1.8倍。然而,如果为建筑物选择一个合适的场地,干扰效应会显著的下降。
Kim et al.(2011)通过风洞试验研究了两建筑间的局部风压系数。考虑了五种不同高度的干扰建筑物。结果表明:主建筑的负压力最小值随着某一干扰建筑物的高度比增加而增加。并且斜列布置相较串列布置会产生更大的负压力。
Hui et al.(2012, 2013a,2013b) 通过风洞试验研究了两个不同形状的建筑物间局部风压系数的干扰效应。使用局部图像测速仪从流场的角度来描述和解释干扰效应。结果表明干扰效应主要取决于建筑物形状和风向。不利位置一般集中在建筑物的边角。建筑物上最大的风压最小值可比单体建筑物上的风压最小值大50%。
目前,对风压干扰效应的研究一般集中在两个没有足够变化范围的建筑物上。研究中很少系统地考虑宽高比和高度比对风压的影响。对于值得注意的并列布置下风压最大干扰效应与建筑物间距之间的关系,目前还没有进一步的研究。
本文采用同步测压技术对某主楼的风压分布进行了系统的研究。干扰效应对风压的影响是一个复杂问题,难以定量分析。因此,采用将每栋建筑的立面分块的方法,研究了两栋建筑串列、斜列、并列布置时的平均压力系数和峰值压力系数分布特征。考虑了BR和HR的干扰效应。此外,还详细分析了干扰效应对并列布置的影响。并且提出了高精度回归方程,给出了最大块干扰因子与建筑间距的关系。
2实验装置
实验在边界层风洞实验室进行。该风洞的试验段宽度为3.0m,高度为2.0m。方形截面模型平面尺寸为100 mm x 100 mm,高度为600 mm(长:宽:高=1:1:6)。缩尺比为1:400,因此该模型表示的是平面尺寸为40mx40m、高度为240 m的全尺寸高层建筑。根据《建筑结构荷载规范》(GB50009-2001),模拟了代表郊区平坦地形、风剖面指数指数为0.16的B类地貌。模型屋顶高度处的平均风速、湍流强度分布和功率谱如图1所示,其中湍流强度分布根据日本建筑物荷载规范(AIJ,1996)进行模拟。
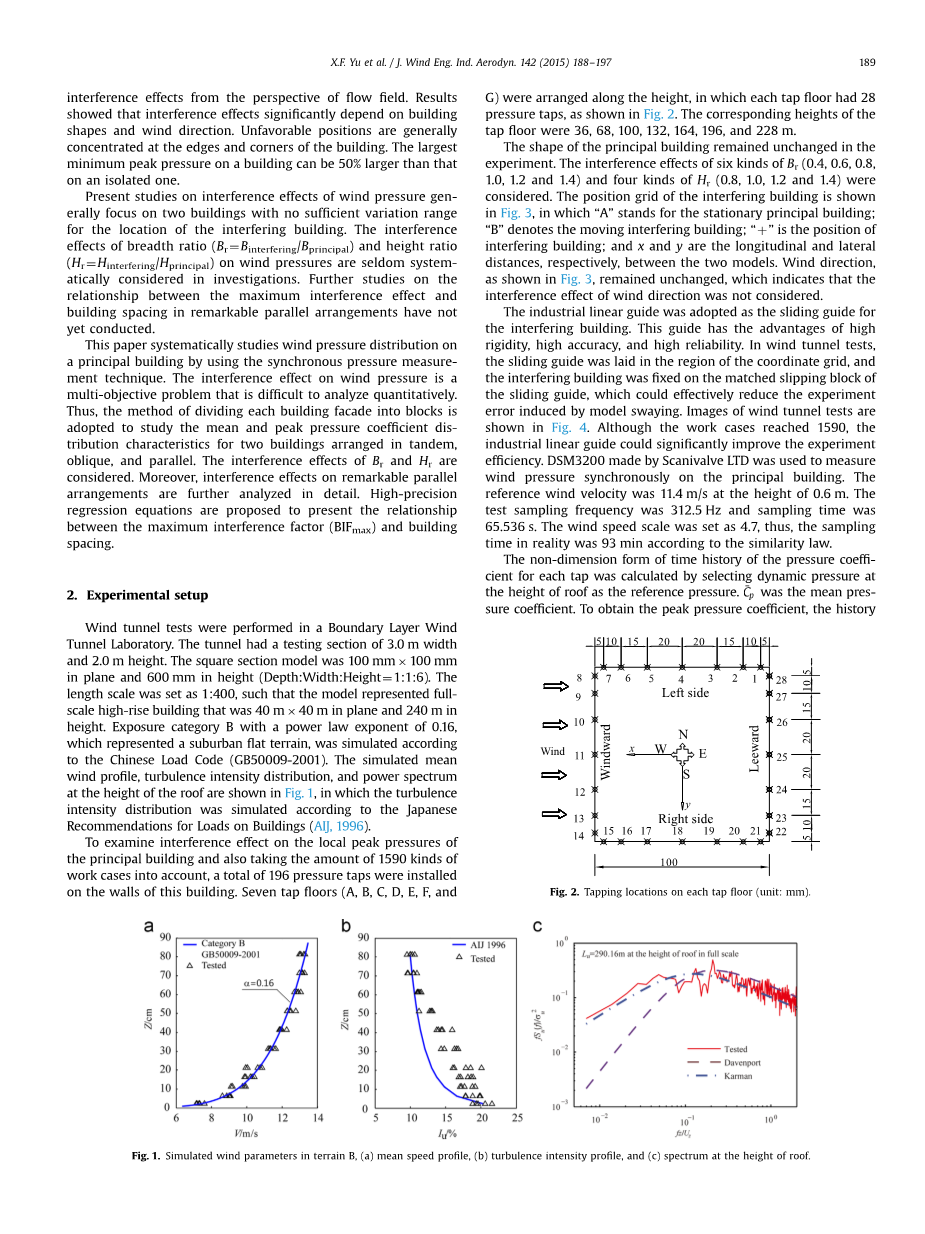
为研究干扰效应对主楼局部峰值压力的影响,同时考虑到1590种工况,在主楼墙壁上共安装了196个测压点。七个测压层(A、B、C、D、E、F和G)沿竖向布置,每个测压层有28个测点,如图2所示。相应的测压层高度分别为36、68、100、132、164、196和228 m。
主建筑的形状在实验中保持不变。共考虑了6种宽度比(0.4、0.6、0.8、1.0、1.2和1.4)和4种高度比(0.8、1.0、1.2和1.4)的干扰效应。干扰建筑物的移动网格如图3所示,其中“a”代表静止的主建筑物;“b”代表移动的干扰建筑物;“ ”代表干扰建筑物的位置;“x”和“y”分别代表两个模型之间的纵向和横向距离。试验中风向角如图3所示固定不变,即不考虑风向角变化对干扰效应的影响。
干扰建筑物采用工业级直线导轨作为滑动导轨。该导轨具有刚性高、精度高、可靠性高等优点。在风洞试验中,在坐标网格区域铺设了滑动导轨,将干扰建筑物固定在滑动导轨的匹配滑块上,有效地减小了模型摇摆引起的试验误差。风洞试验图像如图4所示。虽然测压点数目达到1590个,但工业级导轨可以显著提高实验效率。利用scanivalve公司生产的DSM3200对主楼进行风压同步测量。在0.6米高度,参考风速为11.4米/秒,试验采样频率为312.5赫兹,采样时间为65.536秒,风速标度设置为4.7,根据相似律,实际采样时间为93分钟。
以屋顶高度处的动压力为参考压力,计算了各测压点的历史记录的无量纲形式。Cp为平均风压系数。为了获得峰值风压系数,首先用1s移动平均滤波器对凤压系数的历史记录进行滤波,然后根据《建筑结构荷载规范》(GB50009-2001)(中国建筑工业出版社,2002)规定,按照600s的时间平均间隔将其分成若干段,通过使用基于极值分布类型I(Gumbel分布)的Cook和Mayne(1980)方法可得到极值压力系数是,如下:
A
其中,和分别是极值系数的位置和比例参数,1.4是折减系数,这意味着相应的非磁阻概率为78%。
通过测量管的波动风压的形变已经被调整。 测压管的增益函数和相位函数如图5所示。
主楼的测压点编号为196,总测点达到1590,因此风压数据分析是一项复杂的任务,必须简化。为了显示干扰效应对建筑物之间风压的主要影响,本文将受扰建筑的每个立面根据风压分布特征分为9个区块。每个块中的测点如图6所示。
选择每个区块所有测压点的最大平均风压系数和峰值风压系数来研究受扰建筑物的风压分布特征规律。块干扰因子(BIF)用于描述干扰效应对受扰建筑平均和峰值风压分布的影响。
对于一些特殊的干扰位置和工况,采用每个测压点的干扰因子(IF)来分析风压分布规律。
3.结果和讨论
在分析了基本配置(B=1和H=1)对风压分布的干扰效应后,发现受扰建筑物的平均和峰值风压系数的放大效应区域集中在左侧墙上。(面对干扰建筑物的立面),其中干扰效应在块1(迎风部)是最引人注目的。对于迎风墙,平均风压几乎显示出在中心区域占主导地位的防护效果。对于峰值风压,放大效应在边缘区域占主导地位。因此,本文主要分析了受扰建筑左侧立面特别是块1的风压干扰效应。
3.1宽度比的影响
3.1.1平均压力分布
图7显示了平均风压的BIF分布。对于不同的B,左侧立面(面向干扰建筑物的面)的1(高迎风区)。干扰效果可分为以下几个区域:
屏蔽区域:对于六种宽度比,受扰建筑物的风压屏蔽效果显著。随着干扰建筑物的宽度增加,屏蔽区域扩大,但是集中在ly/bIlt;3的范围内。特别地,串联布置时屏蔽效果更明显。
放大区域:由于狭管效应,并列布置的受扰建筑的风压具有明显的放大效应。 BIF值随着干扰建筑物宽度的增加和建筑物间距的减小而增加。当干扰建筑物在有限的网格位置移动时,BIF的最大值高达2.0,如图3所示。如果采用较小的建筑物 间距,BIF的值可能会变大。
3.1.2峰值压力分布
图8显示了不同宽度比的左立柱1号区块的峰值风压的BIF分布。对于全部六种宽度比,放大效果明显。主要干扰规律如下:
(1)在串列布置中,选择左侧立柱顶部的测压点G7来研究干扰效应。图9显示出了对于不同的宽度比,在测压点G7处的峰值压力系数与建筑物间距x/b的变化。当宽度比小于1时,在测压点G7处的放大效应很明显。当宽度比小于1且建筑物间距为时,遮挡效应占主导地位。当建筑物间距为时,放大效应逐渐占主导。最大峰值压力系数的变化情况在每个变化曲线中显示。最显著的干扰情况是当宽度比为 0.8时,风吸力系数增加了78%(有干扰为-3.82,无干扰的为-2.15)。随着宽度比的增加,对应于最明显的干扰位置的建筑物间距增加,而当Ble;1时,最大的风吸力系数会减小。
在斜列布置中,当干扰建筑物与x坐标轴之间的距离越近时,放大效果越显著,BIF的最大值达到1.48。当宽度比小于1时,放大区域随宽度比的增大而增大;否则,该值将会减小。
(3)在并列布置中,由于狭管效应,在受扰建筑物的左侧立面上出现了显著的放大效应。放大区域和放大效应均随着宽度比的增加和侧向建筑物间距的减小而增加。下文3.3节详细讨论了并列排列的干扰效应。
3.2高度比的影响
本文还分析了高度比对主楼左侧立面(面向干扰建筑物的面)1号区块(高迎风区)的平均和峰值压力系数的干扰影响。采用类似于3.1节中使用的方法。
3.2.1平均压力分布
图10显示了四种不同高度比的受扰建筑的左侧立面上1号块的平均压力系数的BIF分布。
在串列布置中,当高度比大于 1时,受扰建筑物的侧面上的遮挡效应占主导地位。更大的高度比会产生更显著的屏蔽效果。然而,该图还显示当x/b=1.5且高度比为0.8时BIFgt;1,因为在干扰建筑物顶部的高速流动影响受扰建筑物的顶部。为了在视觉上显示三维流动效果,采用每个测点的IF来分析风压干扰效应的变化。图11显示了主楼的迎风面和侧壁上的平均风压的IF曲线。这些部位
具有明显的屏蔽效果,其高度低于干扰建筑物的高度。迎风墙上出现较高的吸力(IF lt;0),而干扰建筑物高度的左右立面出现较大的IF值,最大值达到1.56。在迎风墙的高度大于干扰建筑物屋顶高度的部分,观测到的最大IF值也达到1.25。
在并列布置中,由于狭管效应,左立面上的平均风压出现明显的放大效应。越大的高度比,对应会出现更明显的狭管效应和更大的面积。图12示出了并列布置时不同的高度比下干扰建筑物位于处,受扰建筑左侧立面的IF轮廓.狭管效应随着高度比的增加而增加,而当高度比大于1.2时,IF不会改变。
在斜列布置中,当高度比小于1或者当高度比大于1而干扰建筑位于ly / bl lt;2的区域时,遮挡效应占主导地位。当主楼位于干扰建筑的尾迹区域即|y/b|gt; 2且BIF最大值等于1.1时平均风压的放大效应明显。
3.2.2峰值压力分布
图13显示了各种不同高度比的受扰建筑物左侧立面上1号块的峰值压力系数的BlF分布。从比较分析中得出以下结论:
(1)在串列布置中,当高度比小于1.2,特别是当高度比小于1且建筑物间距非常小时放大效应显著。对于干扰效应来说这种情况是很典型的,这是由于三维流动效应引起的,因为前方干扰建筑物的高度低于受扰建筑物的高度。图14示出了当高度比为0.8并且干扰建筑物位于x / b = 1.5的位置时的峰值压力系数和IF轮廓。在左侧立面的部分,屏蔽效果显著,高度低于干扰建筑物的高度。其余部分的放大效果显著。与孤立情况相比,局部峰值风压增大了53%,最大吸力系数达到-2.75。放大效应在迎风墙的顶部和边缘也很明显,IF值分别为1.09和1.18,图15显示了受干扰情况和孤立情况下压力系数的功率谱密度。发生最大IF(=1.53)的位置。受干扰情况下整个频域的湍流能量都大于单体情况下的湍流能量,这取决于接近干扰建筑物顶部的风流时高速尾流引起的较高湍流强度,
(2)在斜列排列中,放大效应几乎覆盖整个网格坐标。越大的H对应产生越大的放大效应区域。最显著的干扰效应的干扰建筑物的位置集中在x/b=5和x/b=9的轴上,
(3)在并列布置中,观察到左立面的峰值压力系数的显著放大。放大效应随着高度比的增加和建筑物间距的减小而增加。当高度比为1.2时,BIF的最大值达到1.52。图16显示了各种高度比下最不利干扰位置y/b=-1.8处的峰值压力系数等值线,在整个左立面显示峰值压力系数分布,放大效应集中在逆风部分左立面随着高度比的增加而增加。当高度比为1时,最显著的干扰效应发生在左立面的中间部分。但是,当高度比大于1时,在左立面的逆风顶部区域发生显著影响。最大吸力系数达到3.05,与孤立建筑相比增加了45%。
3.3进一步分析并列布置
对平均风压产生显著干扰影响的不利区域集中在左侧立面的逆风部分。仅在两个工况下,平均风压的IF
全文共10059字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2011]


