
英语原文共 20 页,剩余内容已隐藏,支付完成后下载完整资料
2.混凝土与钢的应力-应变关系
2.1混凝土
2.1.1单轴应力行为
在实际情况下,混凝土很少只在一个方向上受力(单轴应力),因为在大多数结构情况下,混凝土在多个方向上同时受到应力。然而,假定的单轴应力条件在许多情况下是合理的。
压应力行为
混凝土的抗压强度通常由高径比为2的圆柱体获得。圆柱体以慢应变速率纵向加载,以在2或3分钟内达到最大应力。标准圆柱体的高度为12英寸(305毫米),直径为6英寸(152毫米),28天的抗压强度通常在2000至8000磅/平方英寸(13.8至55.2N/mm2)之间。也可使用较小尺寸的圆柱体或立方体,特别是用于生产控制,而且这些单元的抗压强度较高。通过试验得到适当的换算系数,可将这些试样的结果换算成等效的标准钢瓶强度值。
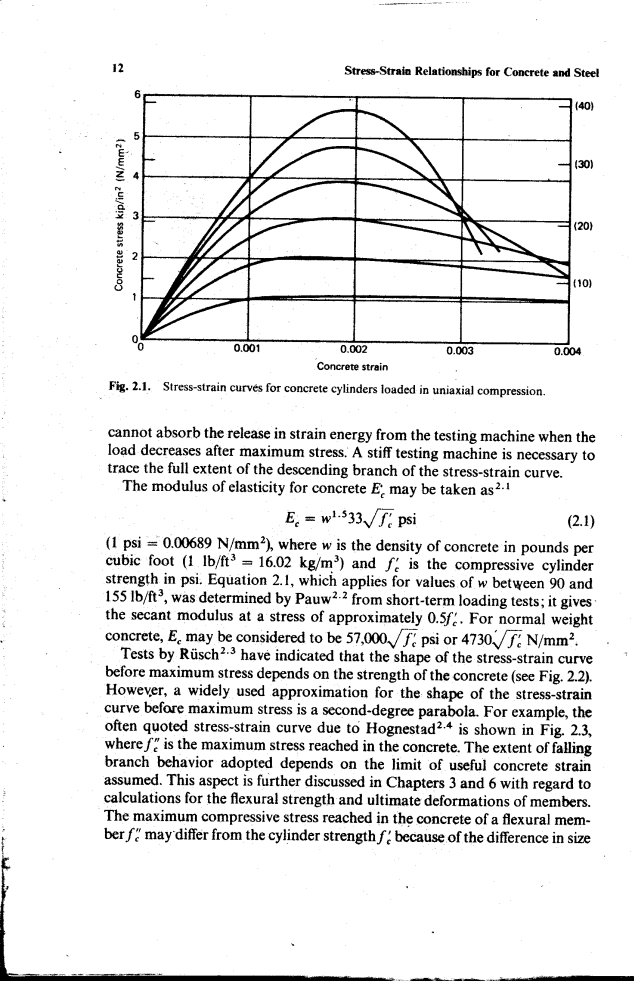
图2.1给出了混凝土圆柱体在单轴压缩下的典型应力-应变曲线,该曲线是在一次长达几分钟的试验中获得的。曲线几乎是线性的,约为抗压强度的一半。高强混凝土曲线的峰值相对较大,而低强度混凝土曲线的峰值较大。最大应力时的应变约为0.002。在较高的应变下,当应力达到最大值时,即使与加载方向平行的裂缝在混凝土中可见,应力仍然可以被承载。在柔性试验机上试验的混凝土有时会发生爆炸破坏,因为当荷载在最大应力后下降时,混凝土不能吸收试验机释放的应变能。为了跟踪应力-应变曲线下降分支的全部范围,需要一台刚性试验机。
混凝土的弹性模量可定为2.1。
(2.1)
(1psi=0.00689 N/mm2),其中w是以磅/立方英尺为单位的混凝土密度(l lb/ft 3-16.02 kg/m3),是以psi为单位的抗压圆柱体强度。公式2.1适用于w在90~155 lb/ft3之间的值,是由pauw2.2从短期加载试验中确定的,它给出了应力约为0.5时的割线模量。对于正常重量的混凝土,EC可被视为57,000psi或4,730 N/mm2。
Ruuml;sch2.3的试验表明,最大应力之前的应力-应变曲线的形状取决于混凝土的强度(见图1)。2.2)。然而,应力-应变曲线最大应力形状的一种广泛应用的近似是二次抛物线。例如,经常引用的由Hognestad2.4引起的应力-应变曲线如图所示。2.3,其中是混凝土中达到的最大应力。所采用的下降分支行为的程度取决于假定的有用混凝土应变的限度。这一点在第3章和第6章关于构件的抗弯强度和极限变形的计算中作了进一步的讨论。受弯构件frsquo;rsquo;c所达到的最大压应力可能由于受压混凝土的大小和形状的不同而与圆柱体强度frsquo;rsquo;c有所不同。在第三章中对混凝土构件的强度进行了较长的处理。
当荷载以较快的应变率作用时,混凝土的弹性模量和强度都会增加。例如,据报道2.5,当应变率为0.01/秒时,混凝土强度可提高17%。
重复的高强度压缩载荷在应力-应变曲线上产生明显的迟滞效应。图2.4给出了辛哈、格斯特尔和图林在慢应变速率下获得的测试数据。他们的测试以及Karsan和Jirsa的测试表明,包络曲线与从单个连续加载应用程序得到的曲线几乎相同。
Ruuml;Sch对无侧限混凝土进行了长期加载试验,发现持续荷载抗压强度约为短期强度的80%,其中短期强度是在持续荷载作用下试件倒塌时在10分钟内加载到失效状态的相同老旧相同浇铸试件的强度。实际上,结构设计中考虑的混凝土强度通常是基于28天的预期短期强度。长期荷载引起的强度下降将至少部分地被混凝土的性能所抵消,从而在较长的龄期达到较高的强度。当混凝土抗压强度达到临界值时,承载力折减系数Q较低。长期加载引起的蠕变应变改变了应力-应变曲线的形状。Ruuml;Sch得到的不同载荷命运下的一些曲线(图.2.5)表明,随着应变速率的减小,最大应力值逐渐减小,但曲线下降的速度较慢,达到最大应力的应变增大。
拉应力行为
混凝土的抗拉强度一般小于抗压强度的20%,可直接从拉伸试样中求得。然而,由于保持试样以达到轴向拉伸的困难和由保持装置引起的二次应力的不确定性,直接拉伸试验很少使用,甚至用于研究目的。
混凝土的抗拉强度可以根据水平放置在试验机中并沿直径加载的圆柱体将开裂的计算拉应力来间接测量。如弹性理论所示,试验方法和沿加载直径产生的应力如图2.6所示。从2P/(pi;HD)关系中求得劈裂时直径的拉应力,其中P为劈裂时施加的载荷,h为圆柱体的长度,d为圆柱体的直径。
混凝土的抗拉强度也可以通过对素混凝土梁进行弯曲试验来评价。梁通常具有6英寸(150毫米)的方形截面。弯曲时的抗拉强度称为断裂模量fr,由弯曲公式M/Z计算,其中M是试件破坏时的弯矩,Z是横截面的截面乘积。劈裂圆柱体的抗拉强度通常为断裂模量的50%~75%。不同之处主要在于受弯构件在即将发生破坏时,混凝土中的应力分布是非线性的。断裂模量的近似关系是
(2.2)
其中.是以psi(l psi 0.00689 N/mm2)为单位的钢瓶强度。对于砂和砾石混凝土,K可以在7到13之间;通常假定K=7.5的下限。显然,抗压强度的增加并不伴随着断裂模量的适当增加。
由于混凝土的抗拉强度较低,在钢筋混凝土构件的强度计算中,混凝土的抗拉强度往往被忽略。然而,当考虑到这一点时,拉伸时的应力-应变曲线可以理想化为一条以抗拉强度为上限的直线。在此范围内,可假定拉伸弹性模量与压缩弹性模量相同。
泊松比
对于混凝土,横向应变与单轴加载方向上的应变之比,称为泊松比,通常在0.15~0.20之间。但是,已确定0.10到0.30之间的值。关于泊松比随混凝土性能的变化,目前尚无可靠的资料,但一般认为高强混凝土的泊松比较低。在较高的压应力下,由于平行于试样内部载荷方向的内部开裂,横向应变迅速增加。在测试失败的试样中所测得的应变如图2.7所示。在大部分加载范围内,试件的体积减小;但在靠近试件抗压强度的高应力下,横向应变得如此之高,以致试件的体积实际上开始增大,这表明强度的破坏。单轴受压试样的破坏一般伴随着平行于载荷方向的劈裂和体积的增大。
2.1.2组合应力行为
在许多结构情况下,混凝土受到多个方向的直接应力和剪应力的作用。考虑到作用在混凝土单元上的力的平衡,可以表明(例如,见Popov),任何组合的应力情况都可以归结为作用于三个相互垂直的平面上的三个法向应力。这三个法向应力是主应力,作用在这些平面上的剪应力为零。
尽管进行了广泛的研究,但对于一般复杂的三维应力状态,混凝土的破坏强度还没有可靠的理论。人们试图对传统的材料强度理论进行修正,但并不是单一的理论能准确地适用于所有的情况。然而,在许多应用中,一种较简单的失效理论给出了足够的精度。
双轴应力行为
如果主应力只在两个方向上作用,即应力在一个平面上作用,而第三个主应力为零,则会产生双向应力条件。图2.8显示了由Kupfer、Hilsdort和Ruuml;Sch发现的导致故障的两个方向的直接应力的组合。研究人员认为,双轴受压混凝土的强度可能比单轴抗压强度高出27%。在相同的双轴压应力下,强度提高约为16 oz。双向拉伸强度近似等于单轴拉伸强度。但是,请注意,拉伸和压缩载荷的联合作用降低了破坏时的拉应力和压应力。
在主平面以外的平面上,直应力伴随着剪应力。莫尔的理论失败,我有一个对这种组合应力情况下的强度的预测。图2.9显示了表示失败的简单压缩和其他组合的莫尔圆是如何形成曲线的。具有与此包络相切或相交的莫尔圆的任何应力组合均可视为失效条件。
Bresler和Pister在图2.10中发现了具有直应力和剪应力的单元的破坏曲线。该曲线表明,在剪应力的作用下,混凝土的抗压强度降低。例如,当存在剪力时,这种作用可能会影响梁和柱受压区的混凝土强度。
三轴压应力行为
在三轴受压条件下,混凝土的强度和塑性都有很大的提高。Richart,Brandtzaeg和Brown发现了轴向加载的混凝土圆柱体在围压作用下强度与破坏的关系。
(2.3)
其中f#39;cc—轴心抗压强度承压试件
- —无侧限试件的轴向抗压强度
fl —侧向围压
Balmer的其他测试给出了横向应力系数的值,范围在4.5到7.0之间,平均值为5.6,而不是Richart等人发现的4.1。在较低的侧压力下,该系数值较大。
图2.11给出了Richart等人在混凝土圆柱体上进行三轴压缩试验时获得的轴向应力-应变曲线。钢瓶受到流体压力的横向限制。对于每一条曲线,流体压力保持不变,轴向压应力增加到破坏,并测量轴向应变。这些试验是在短期内进行的。很明显,侧向压力的增加带来了延性和强度的显著提高。这种影响是由于侧向压力限制了混凝土,减少了破坏前内部开裂和体积增加的趋势。
2.1.3钢筋混凝土约束
在实践中,混凝土可能受到横向钢筋的约束,通常是以紧密间距的钢螺旋或箍的形式。在这种情况下,在混凝土应力较低的情况下,横向钢筋很难受到压力,因此混凝土是不受约束的。当应力接近单轴强度时,混凝土会受到限制,横向应变会因内部逐渐开裂而变得很大,混凝土与横向钢筋相互作用,从而对混凝土产生约束作用。因此,横向钢筋提供被动约束。许多研究人员的试验表明,采用横向钢筋约束可以显著改善混凝土在高应变状态下的应力-应变特性。例如,Richart等人发现等式2.3,就受流体压力约束的混凝土的强度而言,大致适用于受螺旋约束的混凝土。图2.12显示了Lyengar等人测试的三组圆形螺旋约束混凝土圆柱体的应力-应变曲线。每套混凝土都有不同的无约束强度。随着约束钢含量的增加,材料的强度和塑性都有很大的提高。试验表明,圆形螺旋比矩形或方形箍更有效地限制混凝土。在图2.13中,我们得到了由Bertero和Felippa测试的混凝土棱柱的荷载-应变曲线,其中包含了不同数量的正方形关系。不同横向钢含量对延性的影响较大,但对强度的影响较小。
图2.14说明了圆形钢螺旋约束与矩形或方形钢箍约束之间存在相当大差异的原因。圆形螺旋,由于其形状,是轴向环向张力,并提供一个连续的围压周围,这在较大的横向应变近似流体约束。然而,作为一条规则,方形箍只能在箍的角附近施加限制反应,因为混凝土对箍的两侧的压力往往会使侧面向外弯曲,如图2.14所示。因此,相当一部分混凝土截面可以不受约束。由于角点之间的内部拱作用,混凝土仅在截面的角部和中心区才能得到有效的约束。尽管如此,方钢的延展性确实有了显著的提高,许多调查人员也观察到了强度的提高。
从图2.12和2.13可以显然得出,在接近混凝土单轴强度之前,横向钢筋约束对应力-应变曲线影响不大。在高应变时,应力-应变曲线的形状是以下许多因素的函数:
1.横钢体积与混凝土芯体体积之比,因为高横钢含量意味着较高的横向精炼压力。
2.横向钢的屈服强度,因为这为围压提供了一个上限。
3.横向钢筋间距与混凝土芯尺寸之比,因为间距越小,约束效果越好,如图2.15所示。混凝土是由横向钢筋之间的混凝土拱形约束的,如果间距很大,很明显,大体积的混凝土不能被限制,可能会剥落。
4.矩形箍筋或箍筋情况下,横筋直径与横筋无支撑长度之比,因为钢筋直径越大,约束效果越好。这一效果如图2.14所示。由于箍筋的抗弯刚度很小,箍向外弯曲,而不是有效地将混凝土限制在拐角之间的区域,小直径的横杆将仅作为角部之间的纽带。当横杆直径与无支撑长度之比较大时,由于箍侧抗弯刚度较大,混凝土有效约束面积较大。在圆形螺旋的情况下,这个变量没有意义:给定其形状,螺旋将处于轴向拉伸状态,并将对混凝土施加均匀的径向压力。
5.纵向钢筋的含量和大小,因为这种钢筋也会限制混凝土。纵筋通常直径较大,且钢筋直径与无支撑长度之比一般较大,可以有效地约束混凝土。但是,由于横向钢筋对纵向钢筋产生约束作用,必须将纵筋紧贴横向钢筋放置,如果需要纵向钢筋的移动才能使纵筋与横向钢筋有效接触,则会降低约束的效率。
6.混凝土的强度,因为低强度混凝土比高强度混凝土具有更强的延展性(见图2.1)。
7.加载速率,因为混凝土的应力-应变特性是随时间而变化的。
在横向钢筋之外,混凝土不受约束,这种保护层或壳体混凝土应具有与横向钢筋混凝土不同的应力-应变特性。当无侧限强度达到时,覆盖混凝土通常开始剥落,特别是当横向钢筋含量很高时,因为大量横筋的存在核心和覆盖混凝土之间形成了一个脆弱的平面或表面,并加速了剥落。因此,对于高横向钢含量,高应变条件下保护层混凝土的贡献应忽略不计。可以假定保护层混凝土具有无约束混凝土的特性,直至假定的剥落应变,并且在较高的应变下没有贡献。如果横向钢筋含量较低,则保护层混凝土将较不容易剥落,并倾向于与受约束的核心一起发挥更多的作用。在这种情况下,可以对高应变情况下的保护层混凝土进行一些考虑。
下面对钢筋约束混凝土的强度和延性提出了一些建议。
圆形螺旋约束混凝土
假设螺旋线足够近,可以施加近似均匀的压力,围压可以由螺旋钢形成的环向张力来计算。图2.16显示了半个螺旋旋转的自由体。当螺旋钢筋达到屈服强度fy时,混凝土fl所受的侧压力最大。如果ds是螺旋线的直径,Asp是螺旋杆的面积,s是螺旋线的节距,则图2.16所示的作用在螺旋线半圈上的力的平衡要求:
(2.4)
将等式2.4代入等式2.3中,我们看到受螺旋约束的混凝土的轴向抗压强度是
(2.5)
受螺旋约束的混凝土延性的增加也是相当可观的,Lyengar等人根据试验获得的经验数据,提出了受圆形螺旋约束的混凝土的应力-应变关系。
矩形箍约束混凝土
全文共7303字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[1761]


