超磁致伸缩材料悬臂梁的有限元分析外文翻译资料

 2022-10-27 03:10

英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

超磁致伸缩材料悬臂梁的有限元分析

摘要

本文的重点是要突出一些在磁致伸缩材料的成功应用基于微机电悬臂系统（MEMS）中的关键标准(MEMS)。涂层悬臂梁的行为是复杂的，许多作者有使用分析技术提供的解决方案。在这项研究中，有限元分析的软件包进行合并全磁致伸缩应变张量及其与结构力学的偏微分方程耦合求解系统。一个宽范围的几何形状和材料性能被进行求解，去研究悬臂挠度和系统共振频率的影响。后者被使用的特征频率解算器发现。该模型已被调整为比较在该领域内的其他数据，结果也超越了以前的工作。

关键词：有限元建模，磁致伸缩，磁致伸缩作动器、微机电系统（MEMS）。

一、引言

多学科研究的领域如生产设备的基础上，机械，光学，电，磁和流体系统促进了微米尺寸设备的发展及科技。最近几年来，在构建基于电气和机械系统的微米规模的设备有显着的进步，并且有越来越多的商业利益。1999年在美国市场价值的1亿美元的范围内，设备上的微米尺度主要用于传感器和执行器的功能上。该技术的进步正在被许多其他进程使用，如汽车和电信推动前进的应用，全球市场认为在未来两年内会超过八十亿，并预计将增加以每年20％的速度递增。在微机电系统（MEMS）领域内，磁性材料组织正提出一个新类别的磁体，增加了新的功能，并在生物医学、天文学和信息技术领域开拓新的市场。

磁致伸缩材料是一种在外部磁场作用下发生机械变形的材料，磁致伸缩是铁磁材料在与畴壁运动相反的旋转的时刻受部分或全部磁化时的效果呈现。在磁场的影响下，力矩会开始向磁场方向旋转。在一般情况下，这将改变系统的总自由能。该材料在材料内部通过调整组成原子之间的键长和内部应变来最大限度地减少这种变化。这种内部变化会持续到饱和。在开关、阀门、传感器等设备上，磁致伸缩由于具有较高的功率密度、遥控、低性能的退化，简单的制造工艺，更高的响应时间、没有电触点的远程操作的能力等优点，因此比压电元件更实用。双晶片是微机电系统中的一个基本结构，不仅被作为设备使用，也被用做分析方法上如在磁性材料的磁致伸缩常数的标定。这些设备都采用牺牲层的平版印刷技术形成一个电枢，其一端是刚性固定的。这些设备都采用牺牲层的平版印刷技术形成一个电枢，其一端是刚性固定的。

二、背景

许多作者通过寻找材料内部的储存能量为磁致伸缩创造一个完整的数学形式的表达。由 Chikazumi , Kittel, 和 du Treacute;molet de Lacheisserie，以及其他使用的内部能量的最小化来找到由外部磁场产生的内应变。由 Guerrero这些推导中发现的矛盾和Wetherhold通过最小化吉布斯

自由的能量密度，如在定义(1)。这种形式将总的内部能量Utot分别与应力、应变张量，Tij和Eij相结合。

通过(1)的最小值，求出应变张量，如图（2）。该矩阵可以被用来确定从应用程序的外部磁场的方向上的相对于晶轴的余弦一个方向上所产生的机械应变。应变的大小与材料的磁致伸缩常数成正比，并且依赖于结构和晶体取向。此张量是精确的相同的数学形式，如以前的作者的工作。然而，这些被归类为宏观观察到的菌株。现在这个矩阵张量作为机械内部应变能力，允许使用类似的解决方法，已开发弹性材料的能力，并且还允许在同一系统中的其他内部菌株的简单的结合和耦合。它们可以是例如从压电材料和热膨胀产生的压力。

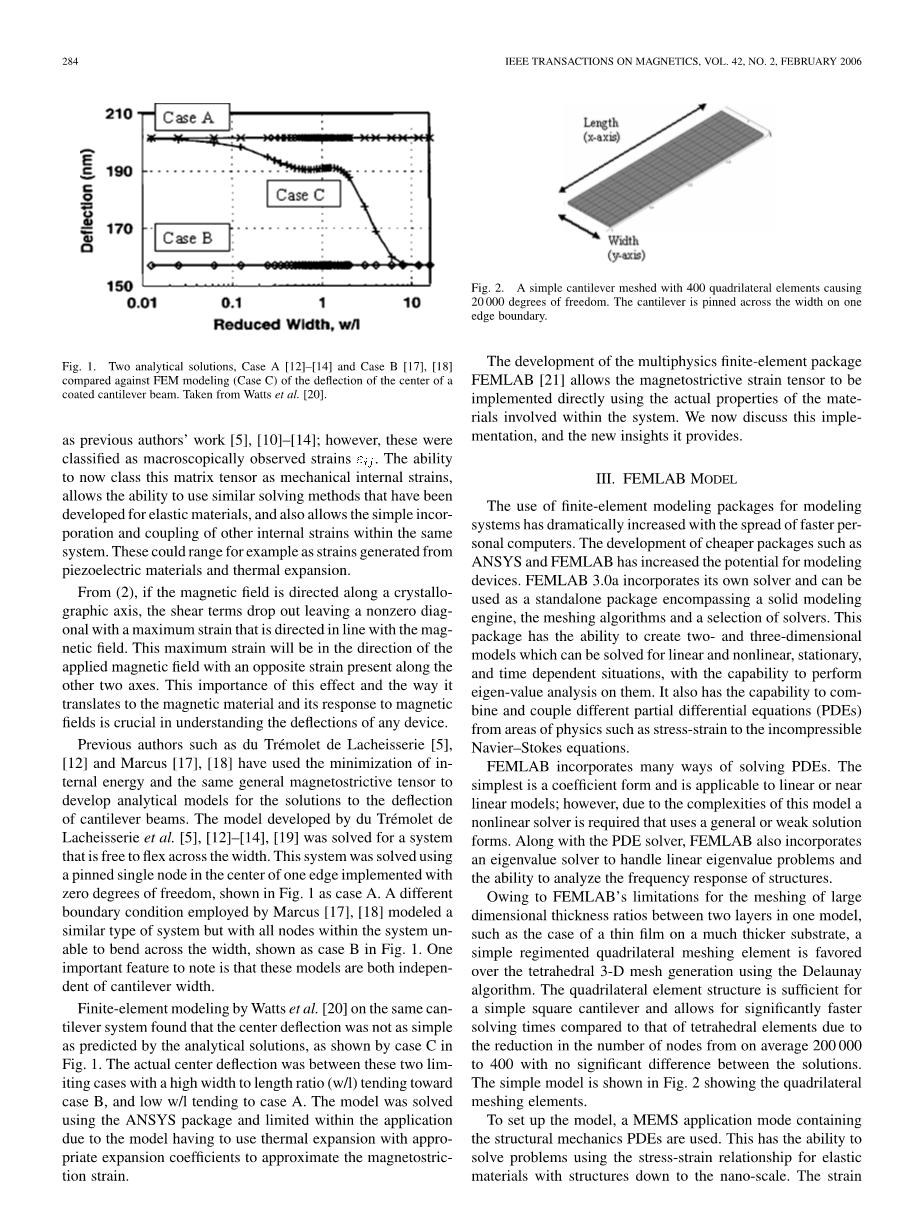
Fig.1. 两种分析的解决方案，方案A和情况B相比对的中心的偏转的有限元建模（情况C）的涂悬臂梁。

从（2）看出，如果磁场沿晶轴定向，剪切项脱落留下一个非零对角与被引导符合磁场的最大应变。此最大应变将在外加磁场的方向上与另一个轴的相对应的应变呈现。这种效果的重要性，和它转化为磁性材料的方式，以及对于磁场的响应，对于理解的任何设备的挠度是至关重要的。

前人如 du Treacute;molet de Lacheisserie和Marcus所使用的内部能量的最小化，并且在同一般磁致伸缩传感器开发的分析模型以解决悬臂梁的偏转问题。du Treacute;molet de Lacheisserie设计的模型被用来解决具有自由的横跨宽度的系统。该系统解决了使用固定的单节点的自由度为零的实现一个边缘的中心，如Fig.1所示为例。由Marcus采用的不同的边界条件建模类似类型的系统，但具有如Fig.1所示的情况下B中的系统内无法在宽度方向弯曲的所有节点。值得注意的一个重要特点是，这些模型都是独立的悬臂宽度。

在由Watts发现的系统中，相同的悬臂有限元建模，该中心挠度不是那么简单由解析解预测，如Fig.1所示的情况C。实际中心挠度这两种极限情况之间的高宽长比（W / L）朝向情况B趋向，和低的W / L趋于情况A。该模型是利用ANSYS包解决，并由于不必使用与适当的膨胀系数的热膨胀来近似磁致伸缩应变模型受限于有限的应用中。

多物理有限元软件包FEMLAB的发展使得磁致伸缩应变张量直接使用系统内所涉及的材料的实际属性来实现。我们讨论这个实现，以及它所提供的新的见解。

三、FEMLAB 模型

个人电脑的普及，大大增加了有限元建模软件包的建模系统的使用。如ANSYS和FEMLAB这类便宜的软件的发展增加了模拟设备的潜力。FEMLAB 3.0A纳入自己的求解器，可以作为一个独立的软件包包括实体建模引擎，网格划分算法和选择求解器。这个软件包有能力创建二维和三维模型，可以解决线性和非线性，固定和时间依赖的情况下，与执行本征值分析的能力。它也有能力将几个物理领域的不同的偏微分方程（PDE）如应力-应变关系不可压缩流动的斯托克斯方程相结合。

FEMLAB软件包含许多方法求解偏微分方程。最简单的是一个系数形式，是适用于线性或附近线性模型，然而，由于该模型的复杂性，该模型的非线性求解器是必需的，使用一般或弱解形式。随着偏微分方程求解，FEMLAB软件还包括一个特征值求解器来处理的线性特征值问题和分析结构的频率响应能力。在一个模型中两个层之间的啮合由于FEMLAB限制为较大的尺寸厚度，如一个厚得多的基片上的薄膜的情况下，一个简单的刻板四边形的啮合元件通过使用四面体的3-D网格生成德劳内算法是有利的。四边形元件结构是足够的一个简单的方形悬臂并允许显著更快解决时间，相比四面体单元由于在节点的数目的减少，从平均200000〜400与溶液之间没有显著差异。Fig.2.显示的是四边形网格单元的简单模型。

Fig.2.一个简单的由400个四边形单元啮合而成的用油20000自由度的悬臂，悬臂被固定在一个宽度上的边界

MEMS的应用模式包含结构力学偏微分方程的应用被用于模型的建立。使用的应力-应变关系有能力解决纳米尺度结构的弹性材料的问题。系统内的应变可以用一个点，变量的位移分量的u、v和w表示。系统内的总应变也可以被分解为热，弹性和内部应变三个附加组件。磁致伸缩传感器在PDE的内部应变内使用。一个有限元模型在使用磁致应变的意义在于，它不需要近似在PDE在板层的变化和减少宽度比。如果在厚钢板工作，那么网格单元的较高密度应引入的厚度方向上实现合适的收敛。厚度对梁挠度的影响是目前正在进行的研究。

磁致伸缩应变张量被纳入只有活动磁层应力应变PDE。然后在两个域的一个边缘的结点给出的零自由度的特性，有效地钉扎结构的边缘，以形成悬臂梁。

由于这个系统是一个复杂的系统，一个固定的非线性求解器被设置一个相对宽容的收敛10。该解算器使用的阻尼牛顿法的不变形式，其中使用了最初估计的解U0。该算法解决了一个线性系统，以形成一个校正delta;U。一个新的估算，以将溶液修正达到收敛直到其可以是迭代形成的方案。为了避免不收敛的系统，25次为迭代的上限，但是，所有的结果在本文从FEMLAB软件在这达到上限之前的融合。

除了这个固定的解算器，一个特征值和频率响应求解器也分别在模型上找到悬臂系统内的无阻尼共振和稳态响应于谐波负载中实现。

一旦求解已经收敛，其结果可能是后处理。这些可以以各种格式来示出;然而，为了简化和速度的边界的可视化应用中，每个表面的边界上的解决节点用于显示所需的表达。此报告的所有模型中所示的后处理的结果表示为这两个正交状态之间的差异。这代表的最大磁致伸缩应变，可以产生的纯力矩旋转90ordm;。

对于不同的有限元建模包和解决的解决方案，一些问题可以导致相同的一组问题的最终收敛的答案之间的差异。这种差异的主要来源是在程序中的数值误差，如从不同的计算程序，包括截断和整个收敛序列的四舍五入错误的结果。其他来源的问题，可以是优化的网格划分的结构，精度的收敛性，和所使用的软件，导致在某些模型中的常数的精确度的程度，高达10%的差异。

四、悬臂梁挠度

如Fig.3.结果从FEMLAB开发的有限元模型显示相比，限制的解决方案如Fig.1所示。采用72 nm的上400米的玻璃基板的坡莫合金，每瓦，不均匀变形是结构的中心和边缘之间产生。在FEMLAB进行的有限元模型和瓦特等人进行的ANSYS模型之间的比较。在Fig.1所示是标准10％的误差范围内。

Fig.3 玻璃衬底上相比以前的解析解的坡莫合金变形。

上述两种限制的情况下，上述模型也同意从这一新的建模，在极端的几何形状的中心区域的偏转得到的偏转。

在一个大的减少的宽度，在中心和边缘挠度有一个显着的差异。这意味着悬臂梁末端是卷曲的，并且对于总挠度减少宽度到0.1是一个显着的贡献。结构的几何形状的刚性支配在卷曲还原，形成了一个平坦的端悬臂。

当W / L接近零，偏转的边缘和中心开始收敛到相同的值 du Treacute;molet de Lacheisserie极限。对于这个系统，如Fig.4（a）所示，观察0.5纳米的宽度变化。在较大的W / L的值，唯一的中心值收敛到 Marcus极限挠度明显差异。这种悬臂的远端边缘是能够弯曲到超过60nm的挠度，如图Fig.4（b）所示。

由于w/l接近统一的中央挠度似乎是固定的，导致形状刚度在40纳米的宽度变化，如Fig.4(C)所示。作为硅衬底比所述磁性材料更硬，在控制挠度的发展，迫使只是边缘弯曲，直至应变是在活性物质大到足以克服硅的硬度。因此，高原增加的活动层变得不那么占主导地位。

Fig.4

对底物的偏转特性关系如Fig.5所示，不同的基板之间的比较是被覆盖的。第一个系统采用一个400米的玻璃基板上而另一个使用相同厚度的Kapton聚酰亚胺衬底。这两个系统都有效地包覆100 nm的坡莫合金作为磁性材料。由于减少刚度的基板，在高原的程度的减少是清楚可见的。此外，边缘向中心挠度的比为W / L = 10玻璃和聚酰亚胺分别为0.685和0.649。由于较硬衬底虽然略有增加经历，这仍然表明边缘的卷曲是悬臂梁系统的固有形状的问题，而不是由于系统内的材料。

Fig.5 2个不同的基板悬臂梁中心挠度的归一化比较

五、频率响应

频率响应求解器可被实现到任何模型来找到该系统的机械响应。为了与先前公布的值进行比较，生成为23mm*8.5mm的悬臂继Guerrero和Wetherhold分析解决方案。

该结构具有一个w/l 为0.37，对应于一个由于形状刚度减少卷曲的系统。结构材料的属性被设置为150米，加上与Tb–Fe的磁致伸缩性能实现1.1米的Terfenol- D活性层的玻璃基板。

特征解算器被用来寻找系统的频率。该解算器不仅能够计算系统的纯弯频率，而且可以计算出扭转模态。

在该系统中，前七个共振模式，以增加频率的顺序进行求解，其中包括四个纯的弯曲模式和三个扭转的如Fig.6所示。解决的值的前七个特征的解决方案是在5%的已发表的分析数据，229Hz，1332Hz，1429Hz，4014Hz，4208Hz，7624Hz，7892Hz。

Fig.6 Guerrero和Wetherhold使用的悬臂系统的前七个特征频率性能的。说明：暗区表示零挠度和白色表示最大挠度

Fig.7一个悬臂系统的频率响应作为频率的函数

其中磁场仅沿着该系统的长度定向

生产弯曲仅纵向模式。

Fig.7表示了悬臂偏转作为频率的函数的幅度。该峰对应于前三纵向弯曲模式，作为磁场一直沿着系统的长度施加在alpha;x= 1。这，由于磁致伸缩矩阵，只有引入纵向模式，因为没有扭转应变诱导。这些模式在频率上间隔开，它们之间没有耦合。

介绍一种旋转磁场引起的扭转振荡。为了简化模型中，使用磁场定在45度，alpha;2x alpha;2y=1，并且表示出重叠在如Fig.8纯弯曲模型。

Fig.8用45度磁场的悬臂频率比较。

纵向弯曲模式的谐振频率是不受掺入的扭转力，然而，第一扭转和二次扭转模式是分别与第二和第三个弯曲模式非常接近的。另一个重要的点要注意的是包含的剪切弯曲条款影响的悬臂的偏转的幅度。如果使用旋转磁场，这种变化将作为一个函数的角度。

要比较这些机械共振是如何取决于前五个弯曲模式绘制作为一个函数的宽度减少，如Fig.9所示。

Fig.9前五个特征频率的悬臂系统绘制为

宽度函数。

虽然只有前五个特征频率绘制，一些重要的功能仍然存

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[153472]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章