英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
Simheuristics算法综述:扩展的元启发式算法
以解决随机组合优化问题
Angel A. Juan a,lowast;, Javier Faulin b, Scott E. Grasmanc, Markus Rabed, Gonccedil;alo Figueirae
a西班牙加泰罗尼亚开放大学IN3计算机科学系
b西班牙纳瓦拉公立大学统计学系和OR
c美国罗彻斯特理工学院工业与系统工程系
d德国图恩多特蒙德生产和物流部IT部门
e INESC TEC和葡萄牙波尔图大学工程学院
摘要:现实生活中的许多组合优化问题(COP)本质上是NP-hard问题,例如物流、运输、生产、医疗保健、金融,电信和计算应用等。这些组合优化问题通常规模庞大,并且需要在短时间内获得高质量的解决方案,因此需要使用元启发式算法。元启发式算法受益于不同的随机搜索和并行化范例,但其通常假设问题的输入、目标函数及约束条件是确定的。然而我们身边都存在不确定性,这往往会使静态模型过分地简化了现实生活中的系统。在对相关工作进行了广泛的审查之后,本文提出了一种利用仿真技术来扩展元启发式算法以解决随机组合优化问题的一般方法。“Simheuristics”算法允许建模者将仿真技术(任何变体)集成到一个以元启发式算法为导向的框架中,以自然的方式处理现实生活中的不确定性问题。这些优化驱动的算法适用于当随机组合优化问题对应的确定性问题已经存在有效的元启发式算法的情况。另外,在对高质量解的选择过程中,Simheuristics算法能更方便的进行风险和可靠性分析。本文将从不同领域中的几个应用实例来说明这种算法的潜力。
关键字:元启发式算法 仿真 组合优化 随机问题
一、概述
我们生活在拥有多式联运系统的大城市,使用复杂互联的机场网络环游世界,在线购买从全球不同地区送至家门口的产品,使用昂贵的电子卫生系统以及通过互联网与朋友和同事们保持联系,我们的生活也与全球金融市场的波动息息相关。 世界变得越来越复杂,然而我们周围的大多数系统却缺乏有效的工具来改善其设计、可靠性和日常的运行效率,因而这些系统在货币成本和环境成本方面表现得很低效。与上述系统相关的大多数决策问题可以归纳为具有不确定性的(随机)NP-hard组合优化问题(COP),元启发式算法能够在相对较短的时间内为这些问题生成高质量的解决方案。从历史上看,它们主要应用于不考虑实际不确定性(即随机或随机行为)的简化场景。然而,将随机性考虑进组合优化问题已经成为一种趋势,来描述系统部分信息事先未知的一类实际问题。这种趋势可以在文献[1]和文献[2]中看到,他们总结出了许多具有随机特征的传统组合优化问题,例如随机路由、随机调度和随机保留。Hem-melmayr[3]等研究了基于随机产品使用的库存路线问题。关于使用元启发式算法解决随机组合优化问题的完整调查可以在文献[4]中找到,作者按照目标函数的估计方式将这些方法分为两大类:(i)特设近似;(ii)仿真。
仿真技术允许以自然的方式对复杂系统进行建模和人工复制[5,6]。因此可以将细节融合到这些模型中,而不需要进行复杂的数学描述,且计算时间通常可以控制,但是复杂的模型可能需要很长的开发时间且难以验证。另外,仿真本身并不是一个优化工具,因此需要设计仿真实验以便了解模型在决策和概率空间方面的行为。目前已经设计的实验[7]是此类研究的第一步,有助于确定解空间的较优区域或进行敏感度分析,但大型组合优化问题就需要使用元启发式算法进行有效的搜索。本文通过提出一类称为“Simheuristics”的新型优化算法,扩展了以往将仿真与元启发式算法相结合的工作,这些算法将仿真(在其任何变体中)集成到一个元启发式驱动的框架中以解决复杂的随机组合优化问题。
元启发式算法与其他方法的混合算法作为解决复杂组合优化问题的一个很好的途径[8]在运筹学的研究中已经得到了广泛的应用。Bianchi[4]等介绍了早期的例子,Glover[9, 10]和April[11]等通过开发商业优化软件OptQuest,推动了仿真和元启发式算法的结合[12]。为了使OptQuest具有通用性并与任何仿真模型兼容,作者针对连续和离散优化问题提出了一种“黑匣子”方法,即求解程序完全与系统分离。这种方法主要面向优化系统的仿真模型,即为给定系统生成离散事件或Monte Carlo仿真模型,然后使用OptQuest软件优化系统的控制参数[13,14]。但是正如文献[15]所描述的那样,有些方法不适用于开箱即用。相反,他们需要适应问题的具体特点。在这些情况下,基于OptQuest等封闭式软件的解决方案可能不是最有效的解决方案。
在本文中,我们讨论将仿真与元启发式算法相结合的不同方式,以及如何使用问题特定信息来优化解决方法。我们的启发式方法有两个鲜明的特点:
1. 它促进了优化和仿真之间更紧密的结合。 尤其体现在解决方案的评估不仅通过仿真来执行,而且还通过特定问题的解析式来执行。因此,它将仿真和临时逼近相结合,避免了通用元模型,尽管这些模型的简单性质对于优化而言很有吸引力,但它们并不能准确地表示真正的底层系统。
2. 仿真的输出不仅可用于评估解决方案,还可用于改进分析部分,以便后者能够生成和/或评估更现实的解决方案。
本文描述的Simheuristics算法侧重于随机分量(离散)组合优化问题的解决。 这些随机分量可以位于目标函数或约束集中。在优化过程中,我们的方法受益于确定性组合优化问题已有的元启发式算法。如文章第三部分所示,我们的Simheuristics算法已经能够为包括车辆路线规划、调度、制造、系统可靠性和医疗保健在内的不同应用领域的组合优化问题提供最先进的解决方案。如后面将要讨论的,元启发式算法与仿真的结合也促进了在评估随机组合优化问题的替代解决方案时风险分析标准的使用。最后,针对Souml;rensen[16]批判的关于在元启发式算法领域缺乏创新性的问题,本文还旨在通过扩展元启发式算法来“开放”一个新的研究路线,以便通过与不同仿真技术的整合来解决一系列现实生活中充满不确定性的新问题。
本文的结构如下:部分二提出了一种仿真优化方法的分类,并以此将Simheuristics算法归类。部分三回顾了模拟优化方法在不同领域的最新应用,包括:制造和生产、物流和供应链管理以及医疗保健。紧接着是部分四,阐述了Simheuristics算法的主要思想,即将仿真集成到元启发式驱动框架中,从而以自然的方式处理现实生活中的不确定性问题。部分五讨论尚未充分进行探索的进一步的设计问题。部分六向不同行业提供应用示例,包括:生产、物流和互联网计算等。最后,部分七总结了这项工作的主要成果,并对Simheuristics算法未来的研究路线提出了建议。
二、Simheuristics算法——一种仿真优化算法
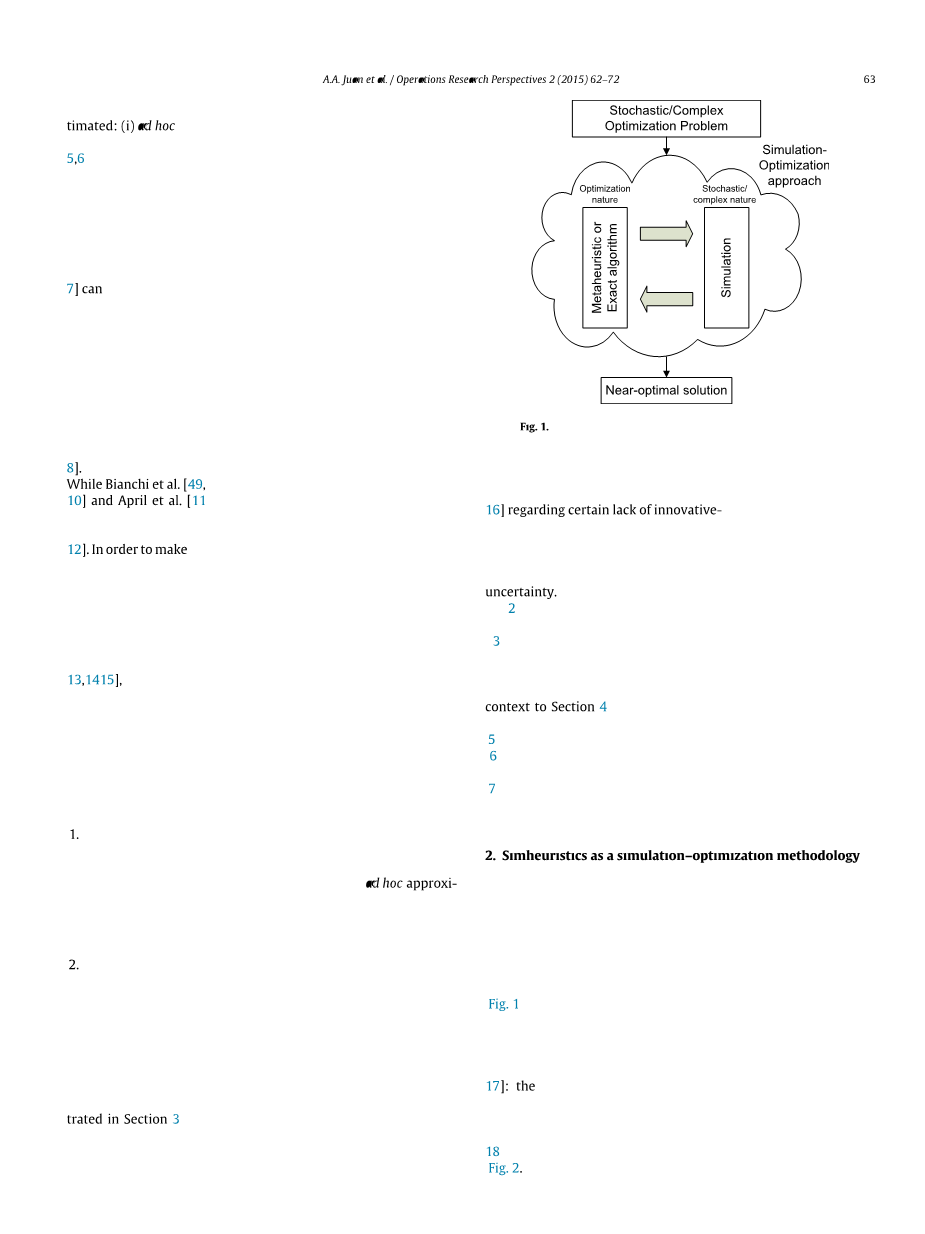
自从50年代提出第一种排序选择和随机逼近方法开始,混合仿真优化(Sim-Opt)技术和方法已经使用了几十年。然而,该领域在过去十五年左右的时间里蓬勃发展,很大程度上是受到计算能力的提升、先进优化方法(如混合元启发式算法)的开发以及仿真软件的出现和传播的影响。图1说明了先前引入的Sim-Opt方法,其中两种技术相互作用以找到复杂或随机优化问题的近似最优解。
随机/复杂优化问题
仿真优化
方法
仿真
元启发式或
精确算法
近优解
图1.仿真优化方法的模式概述
从本质上讲,Sim-Opt方法是由仿真模块和优化模块彼此独立开发再相互结合的方法[17]:仿真模块开发了“仿真优化”(SO)方法——专注于优化仿真模型,而优化模块开发了“混合仿真——分析”(HSA)模型/建模[18]。一般分类方式如图2所示。
图2.仿真优化方法分类
来源:改编自文献[17]
关于这一点,Swisher[19]等将其定义为“确定最优输入参数值的结构化方法”,其中最优值与仿真模型相关联,且由函数的稳态或瞬态输出得到。因此,优化程序使用来自仿真模型的输出,用来评估给定解决方案的性能。该解决方案由一系列决策组成,这些决策是仿真模型的输入变量。优化程序在对解决方案评估的基础上,并参考过去的数据决定一组新的输入值。因此,仿真模型充当优化过程的评估函数(EF)[20], 或者可以模拟几组输入值(每个都是问题的解决方案)以构建替代模型(或元模型)(代理模型构建,SMC),然后就可以使用经典优化技术而不是仿真来解决[21]。将元模型的解决方案视为对原始问题的近似解决方案,文献中的几篇论文讨论了EF和SMC方法[22–24]。商业优化软件OptQuest [9,25]将这两种方法相结合,在这个软件中,EF组件包含两个元启发式算法(分散搜索和禁忌搜索)的组合,而SMC组件使用神经网络。
就HAS而言,根据Shanthikumar和Sargent [18] 的研究,HSA模型是“一个结合了可识别仿真和分析模型的数学模型”,而HSA建模包括建立整个系统的独立分析和仿真模型,开发他们的求解程序,并使用这些求解程序以解决问题。 HSA模型的一个例子是带有采样场景的任何随机程序(通过Monte Carlo仿真获得)。因此,HAS模型通常不用于评估解决方案的质量或可行性,而是用于改善分析模型(AME)或生成部分解决方案(SG)。在AME中,仿真用于改进特定问题的分析模型的参数。 这种增强分析模型的策略往往比EF更少地使用仿真,因为优化组件不依赖于仿真来验证其行为。事实上,在图二中当我们从左向右移动时,更多特定问题的信息被汇总,优化对仿真的依赖性往往会降低。
值得注意的是,当在图二中考察仿真和优化之间的等级结构时,我们可以区分出更多的优化驱动和仿真驱动方法。在前者中,优化算法是“驱动”代理,仿真充当“辅助”代理,在适当的时侯被优化代理(基于仿真的优化)调用。在后者中,仿真充当驱动代理以再现随机系统的行为,然后不时地调用优化以便找到一些仿真参数的最优(或接近最优)值(基于优化模拟)。最后,如图2所示,Simheuristic算法是Sim-Opt方法的一种特殊情况,而这类方法通常是优化驱动的,可以根据其具体实现分类为EF(SO)或AME(HSA)。
三、混合仿真优化技术(Sim-Opt)的应用
Simheuristics算法作为Sim-Opt方法的一种特定类型,为了展示其潜在的应用领域,本节回顾了不同领域的Sim-Opt方法的最近应用(都基于精确和近似优化方法)。应用领域包括:制造和生产、物流和供应链管理以及医疗保健。
1. Sim-Opt在制造和生产中的应用
在科学文献中,可以找到制造和生产领域中Sim-Opt方法应用的多个例子。 Dengiz[26]等提出了禁忌搜索算法,并结合实时系统的仿真模型,寻找满足生产需求的看板的最佳数量。Altiparmak[27]等提出了一种混合方法来为异步组装系统找到接近最优的缓冲区大小,他们的方法是将人工神经网络模型与模拟退火结合起来,前一个模型用于开发滤出元模型,有助于解决仿真运行非常耗时的问题。 Byrne 和Hossain[28]对作业车间系统中的生产计划问题应用递归仿真优化方法,递归仿真优化方法在仿真和优化模型之间交替,仿真和优化都不是驱动代理,而是交替进行。仿真的目的是计算调整后的生产能力(考虑系统中的等待时间)并在分析模型时对其进行改进。文献[29]给出了仿真递归优化方法在产品集群、模拟长度和库存水平监控等方面的一些改进措施。Can[30]进行了用于优化随机缓冲区分配问题的不同算法的比较研究,他们的实验结果表明,通过在搜索过程中允许生成不可行解及结合线性惩罚函数可以提高这些算法的性能。Hubscher-Younger[15]等使用MATLAB并通过集成方法优化化学药品的批量生产过程,该方法结合了连续时间、离散事件和状态转换系统。文献[31]研究了复杂装配线上的调度问题,特别是他们认为这个问题通常被称为多模式、资源受限、多项目的调度问题。为了解决这个问题,他们提出了一种基于自组织和仿真的分散启发式算法。Laroque[32]等提出了一种新的由仿真和元启发式算法相结合的混合算法,其中算法的快速收敛程序旨在优化与仿真模型相关的参数。他们将粒子群优化算法和遗传算法的组合作为分布式仿真环境中的实验设计,这些作者使用简单的物料流动仿真模型来评估组合过程给出的解决方案。Almeder和Hartl[33]研究了与金属加工行业的实际生产过程有关的调度问题,可以被描述为具有有限缓冲器的离线随机柔性流程问题,作者提出了一种可变邻域搜索方法,其中目标函数通过Monte Carlo仿真或详细的离散事件仿真进行评估。Lin and Huang [34]解决了半导体制造工厂中自动化物料处理系统设计的问题,他们用仿真模型表示随机复杂的制造过程,并使用粒子群优化算法进行优化处理。该算法通过使用最优计算量分配方法来提升性能,减少了仿真运行的次数。最后,Gansterer[35]等为递阶生产计划提供了一个Si
全文共31656字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16291],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。